Probleemstelling
Oberwolfach is een klein plaatsje in het zuidwesten van Duitsland. Op een conferentie over grafentheorie in dit dorpje stelde de wiskundige Gerhard Ringel in 1967 een vraag die later bekend zou worden als het Oberwolfach probleem; een probleem dat tot op de dag van vandaag nog onopgelost is. Het probleem verscheen volgens [2] voor het eerst in lijst met onopgeloste problemen van [1].
Beschrijving van het probleem
Het originele Oberwolfachprobleem heeft een makkelijke praktische uitleg: aan een ronde tafel zitten n mensen naast elkaar die voor zoveel mogelijk opeenvolgende dagen aan die tafel willen dineren zonder dat ze op een bepaalde dag naast iemand zitten naast wie ze op een eerdere dag al hebben gezeten. Kan het zo zijn dat als je met n personen bent dat je op een bepaalde dag naast alle overige personen precies een keer hebt gezeten?Meer wiskundig gezien kun je naar de complete graaf Kn kijken en jezelf afvragen of je een opdeling van alle edges kunt vinden in allemaal disjuncte cykels van lengte n.
De eerste opmerking die je over het probleem kunt maken is dat er geen oplossing van het probleem is als n even is. Als je als willekeurig persoon elke dag naast twee andere mensen wil zitten dan heb je altijd naast een even aantal dinergangers gezeten. Jezelf erbij opgeteld moet je na elke dag nog naast een oneven aantal personen zitten. Op een gegeven moment moet je nog naast een iemand plaats nemen, terwijl aan twee kanten van jezelf iemand zal moeten zitten. Dit is niet mogelijk.
In plaats van tevreden te zijn met dit partiele resultaat heeft men besloten de vraagstelling van het probleem uit te breiden. Voor een even aantal personen kun je jezelf gaan afvragen of het voor iedereen mogelijk is om op achtereenvolgende dagen steeds naast twee andere personen te zitten, zodat je op het eind met een persoon nog geen kennis hebt gemaakt. In wiskundetaal: als we een 1-factor uit de graaf Kn weglaten is er van de overgebleven graaf dan een opsplitsing mogelijk in allemaal disjuncte cykels van lengte n? Dit probleem staat ook wel bekend als het Nearly Oberwolfach Problem.
Het probleem is nog op een andere manier uit te breiden. In plaats van dat iedereen naast iedereen gezeten wil hebben op een tafel, kun je ook gaan kijken hoe het probleem zich gedraagt als je meerdere tafels hebt van verschillende groottes. Het doel blijft gewoon hetzelfde. Dit probleem noteren we als OP(n;a1,a2,...,am), waarbij n het aantal personen is, m het aantal tafels en ai de grootte van de i-de tafel. Voor een nog kortere notaties: als we aik noteren, bedoelen we dat er k tafels zijn van grootte ai. Merk op dat we met deze notatie het Nearly Oberwolfach Problem kunnen noteren als OP(n;n-2,2).
Oplossingen voor het 1-tafelprobleem
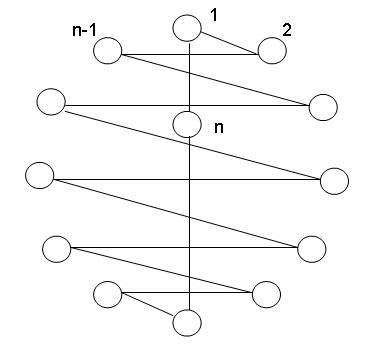
Voor het 1-tafelprobleem met een oneven aantal mensen is er een algemene oplossing. We schetsen het bewijs zoals dat in [2] gegeven is. Zie hiervoor ook onderstaande figuur.

In bovenstaande graaf is vertex 1 met 2 verbonden; vertex 2 met n-1, vertex n-1 met 3, vertex 3 met n-2 etcetera. Verder is vertex 1 verbonden met de "speciale" vertex n en is n op zijn beurt weer verbonden met (n+1)/2. Noem deze Hamiltoniaanse cykel R en zij a de permutatie (n)(1 2 3 ... n-1). Dan geeft { ai(R) | i = 1,...,(n-1)/2 } een Hamitoniaanse decompositie van Kn.
Ook voor het 1-tafelprobleem met een even aantal mensen is er een algemene oplossing. We schetsen wederom het bewijs zoals dat in [2] gegeven is. Zie hiervoor onderstaande figuur.
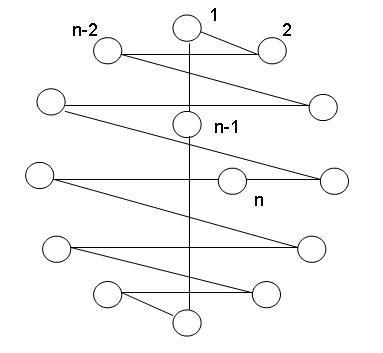
De nummering in deze graaf is exact hetzelfde behalve dan dat vertex [(n+1)/4] en vertex n - [n/4] (waarbij met [x] het eerste gehele getal groter dan x bedoeld wordt) niet met elkaar verbonden zijn maar met vertex n. Noem deze Hamiltoniaanse cykel R en zij a de permutatie (n-1)(n)(1 2 3 ... n-2). Dan geeft { ai(R)| i = 1,...,(n-2)/2 } een Hamiltoniaanse decompositie van Kn - F waar F de 1-factor { [n-1,n], [i,i+ (n-2)/2 ] : i = 1, 2, ..., (n-1)/2 } is.
Kirkman's schoolgirl problem
Hoewel het Oberwolfach probleem in 1967 door Gerhard Ringel werd gesteld, was er wel een enigszins verwant probleem, wat al tijden bestond. In 1850 stelde de wiskundige Thomas Kirkman in het tijdschrift The Lady's and Gentleman's Diary de volgende vraag:
Als vijftien meisjes zeven dagen lang in groepen van drie gaan wandelen; hoe kun je dan een indeling maken zodat niemand meer dan een keer met elkaar wandelt?
Meer algemeen zouden we kunnen kijken naar hetzelfde probleem maar dan met 3n meisjes, waar n een natuurlijk getal (we hebben een drievoud aan personen nodig omdat er anders meisjes - alleen of met twee - op school moeten achterblijven en dat zouden we niet willen). Volgen we de eerder ingevoerde notatie dan heet dit probleem O(3n;3n) We kunnen vrij simpel opmerken dat dit probleem geen oplossing heeft voor even n. Kijk maar naar een willekeurig persoon, bijvoorbeeld de eerste. Op de eerste dag loopt ze met twee andere personen, bijvoorbeeld twee en drie (nummering doet er niet toe); daarna loopt ze met vier en vijf, zes en zeven, etc. tot en met 3n - 2 en 3n - 1. De volgende dag heeft ze een probleem: ze wil met twee medeleerlingen op pad gaan, maar er is er nog maar eentje over. Kortom, er bestaat geen oplossing.
Steiner triple systems
Een met het Kirkman Schoolgirl's problem gerelateerde vraag is wanneer er een Steiner Triple System bestaat. Een Steiner Triple System bestaat uit een verzameling X van n punten en een collectie B van deelverzamelingen van X met precies drie elementen, zodanig dat elke twee punten van X gezamenlijk maar in een element van B zitten. Een Steiner Triple System met n punten (van orde n) noteren we ook wel met STS(n). Er bestaan alleen STS'en als n = 0 of n = 1 of 3 modulo 6. Een bewijs hiervoor kan gevonden worden in [3].
Hoewel Kirkman's existentiebewijs van de Steiner Triple System's voor n = 1 of 3 modulo 6 een mooi resultaat opzich is hebben we er voor het schoolmeisjesprobleem maar gedeeltelijk wat aan. Het bestaan van STS(3n) met n oneven geeft ons goede hoop dat er een oplossing is van O(3m, 3m) met m oneven. Toch zit er een extra eis aan het bestaan aan van een oplossing van het Schoolgirl Problem: niet alleen moet de STS van de gegeven orde bestaan, maar ook moet er een partitie van de drietallen uit B in parallelle klassen bestaan zodanig dat elk punt in precies een van de elementen van elke parallelle klasse voorkomt. Als dit gebeurt noemt men de oplossing een Kirkman systeem. Hieronder staat een Kirkmansysteem met n = 9.
Ray-Chaudhuri en Wilson bewezen volgens [5] in 1971 in [4] dat er een Kirkmansysteem bestaat voor elk getal dat 3 modulo 6 is. In [6] hebben Alspach, Schellenberg, Stinson en Wagner een uitbreiding van deze stelling bewezen: deze zegt dat Kn een Ck factorisatie heeft als n oneven is en k een deler is van n. Dit komt overeen met het feit dat Kn een C3 factorisatie heeft als n een oneven drievoud is, i.e. n = 3, 9, 15, ... . In hetzelfde artikel wordt bewezen dat als uit een complete graaf Kn een 1-factor wordt weggehaald, de graaf opgedeeld kan worden in 2-factoren bestaande uit m-cykels als n een even veelvoud is van m; n ongelijk aan 4m en n groter dan zes. In [7] wordt bewezen dat O(6; 32) en O(12, 34) geen oplossingen hebben.
Uiteindelijk wordt in [8] door Hoffman en Schellenberg een compleet resultaat gegeven voor het uniforme Nearly Oberwolfach Problem (i.e. O(n; ak) met n even en a*k=n): alleen OP(6; 32) en O(12, 34) hebben geen oplossing.
Resultaten voor twee en drie tafels
Tot nu toe hebben twee grote klassen van het Oberwolfachprobleem compleet behandeld: het 1-tafelprobleem, waar we een bewijs van de oplossing hebben gegeven en het uniforme Oberwolfachprobleem (wat feitelijk een uitbreiding van het 1-tafelprobleem is) waarbij we een overzicht hebben gegeven wat de stellingen die tot het volledig bewijs hebben geleid. Dit zijn niet de enige gevonden resultaten van het probleem; met name voor het 2- en 3-tafelprobleem bestaan een hoop deelresultaten.
Een van de 2-tafelproblemen die opgelost is, is OP(2m+2;m,m+2). We zullen kijken naar het geval waarbij m even is omdat bij het bewijs hiervan mooi gebruikt gemaakt wordt van het 1-tafelprobleem. We zullen hierbij het bewijs volgen zoals dat beschreven is in [9]; daar staat ook het geval voor m oneven uitgewerkt (wat feitelijk neerkomt op het vinden van een combinatie van een geschikte 1-factor, een vertex-disjuncte m en m+2 cykel en een goede permutatie; zoals eigenlijk ook gedaan in het bewijs van het 1-tafelprobleem voor een even aantal personen).
Laat G en H grafen zijn met disjuncte vertices V(G) en V(H) en edges E(G) en E(H). Definieer nu G V H als graaf met vertices V(G) verenigd V(H) en edges E(G) verenigd E(H) verenigd { (g,h) | g uit V(G), h uit V(H) }. Zij m nu groter of gelijk aan 4 en even. We bewijzen nu dat er en (m,m+2)-2-factorisatie is van Kmc V Cm+2. Hierbij is Kmc gedefinieerd als het complement van Km ofwel de graaf bestaande uit m vertices en geen edges.
Geval:m = 0 modulo 4. Nummer de vertices uit Kmc met a1,a2,...,am en de vertices uit Cm+2 met b1,b2,...bm+2. Bekijk de m+2 cykel (a1,b1,b2,b3,a2,b4, a3,b5,...,am/2,b(m+4)/2) en de m-cykel (a(m/2)+1,b(m+2)/2,...,am,bm+2). Laat hier vervolgens de permutatie (b1,b3,...,bm+1)(b2,b4,...,bm+2) op los. Dit geeft een (m,m+2)-2-factorisatie. Alle ai'tjes staan tussen een even en een oneven bi'tje in en de reeks van drie bi'tjes in de m+2 cykel zorgt dat de bi'tjes samen een Cm+2 gaan vormen.
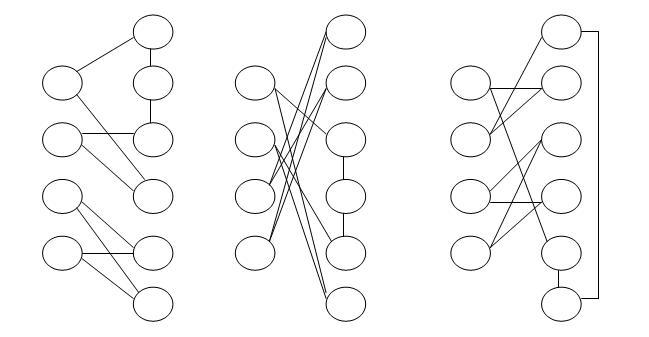
(m,m+2)-2-factorisatie van K4c V C6 met aan de linkerkant van boven naar beneden a1,a2,a3 en a4 en aan de rechterkant van boven naar beneden b1,b2,b3,b4,b5 en b6.
Geval: m = 2 modulo 4. Nummer de vertices uit Kmc met a1,a2,...,am en de vertices uit Cm+2 met b1,b2,...,bm+2. Bekijk de m cykel (a1,b1,b2,b3,a2,b4,a3, b5,...,a(m-2)/2,b(m+2)/2) en de m+2 cykel (am/2,bm+4/2,...,am,bm+2). Laat hier vervolgens de permutatie (b1,b3,...,bm+1)(b2,b4,...,bm+2) op los. Dit geeft een (m,m+2)-2-factorisatie. Alle ai'tjes staan tussen een even en een oneven bi'tje in en de reeks van drie bi'tjes in de m cykel zorgt dat de bi'tjes samen een Cm+2 gaan vormen.
We zijn nu klaar om het algemene geval te bewijzen. Zij A = Km met V(A) = {a1,a2,...,am} en B = Km+2 met V(B) = {b1,b2,...,bm+2} waarbij V(A) doorsnede V(B) leeg is. Laat F' een 1-factor in A zijn en F'' een 1-factor in B. Zij C = K2m+2 - F met V(C) = V(A) verenigd V(B) en F de 1-factor gedefinieerd door E(F) = E(F') verenigd E(F''). Uit de graaf C kunnen we nu (m-2)/2 (m,m+2)-2-factoren halen. Immers, met de oplossing van het 1-tafelprobleem kunnen we uit de deelgraaf A - F' (m-2)/2 m-cykels halen en uit de graaf B - F'' m/2 m+2-cykels. Dit doen we, behalve dan dat we precies een m+2-cykel laten zitten. De graaf die nu over blijft is Kmc V Cm+2; hiervan hadden we hierboven een (m,m+2)-2-factorisatie gevonden. Daarmee is het resultaat bewezen.
Lijst met oplossingen
In [10] staat een lijst met bekende oplossingen van het Oberwolfachprobleem. Het gaat hierbij om:
Onoplosbaarheid van problemen
In [14] wordt (wederom met een verwijzing naar [15]) gezegd dat alle problemen met de som van de lengte van de cykels kleiner of gelijk aan 17 een oplossing hebben met uitzondering van OP(6;3,3), OP(12;3,3,3,3), OP(9;5,4) en OP(11;5,3,3). In het geval van OP(6;3,3) is dit niet heel moeilijk in te zien. Bekijk de graaf K6 en haal er twee disjuncte C3's uit. De overgebleven graaf is dan isomorf aan K3,3. Hier moeten we wederom twee disjuncte C3's uithalen, maar dat kan niet, want K3,3 is bipartiet.
Bovenstaande oplossing is nog vrij kort, maar een oplossing van bijvoorbeeld OP(9;5,4) - die hier te vinden is - is al snel een stuk langer. In [2] wordt vanaf pagina 21 geprobeerd om OP(11;5,3,3) op te lossen, maar op een gegeven moment kun je er bijna niet meer omheen om de computer als hulpmiddel te gebruiken. Bij een relatief kleine toename van het aantal tafels en de grootte van de tafels wordt het probleem kennelijk al zoveel moeilijker dat het (zolang er geen algemeen bruikbaar argument gevonden wordt) bijna niet te doen is handmatig te bewijzen dat het probleem geen oplossing heeft.
Referentielijst