Singularity Knots

Consider a singularity at 0 of an algebraic curve in the complex plane

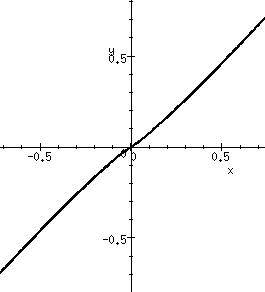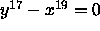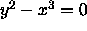
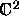. By identifying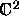

with

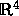the curve can be viewed as a 2 dimensional surface over the real numbers. The intersection of this surface with a small sphere in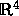

with center 0 consists of a number of closed curves over the real numbers. After applying a projection from this sphere (which is 3 dimensional over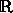

) to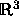

a set of closed curves in

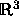is obtained. See also: E. Brieskorn, H. Knörrer: Ebene Algebraische Kurven, Birkhäuser 1981.

Click on the picture to view the corresponding knot.

An animation of this singularity knot. In this animation the singularity knot in the sphere in

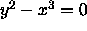
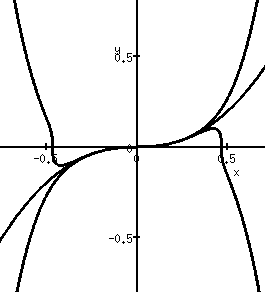
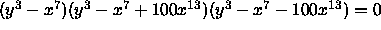
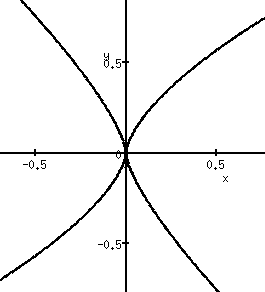
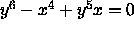
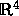is not moving. Only the projection point to map the knot to

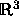is moving.