Gelfand Transform and Spectral Radius Formulæ for Ultrametric Banach Algebras

Nicolas Maïnetti
LLAIC1 Université d'Auvergne
IUT Département d'Informatique, Les Cézeaux
BP 86 63172 Aubière Cedex
France

Date:

Abstract:

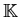
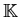
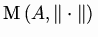
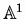
Let $\Bbb K$ be an algebraically closed field, complete for a non-trivial ultrametric absolute value, and let A be a commutative normed $\Bbb K$-algebra with identity. We call multiplicative spectrum of A the set $\mathscr{M}(A,\Vert\cdot\Vert)$ of continuous multiplicative semi-norms on A. We denote by $\Bbb A^1$ the set of multiplicative semi-norms on the polynomial algebra $\Bbb K[X]$. Both sets of semi-norms are endowed with the topology of pointwise convergence. 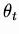For any element t of A, we denote by $\theta_t$the evaluation homomorphism from $\Bbb K[X]$ to A. 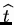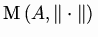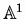We call the Gelfand transform of t the mapping $\widehat t$ from $\mathscr{M}(A,\Vert\cdot\Vert)$ to $\Bbb A^1$ defined by $\widehat t(\varphi)=\varphi\circ\theta_t$. 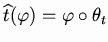We then call spectrum of t the subset of $\Bbb A^1$: $\sigma(t)=\widehat t(\mathscr{M}(A,\Vert\cdot\Vert))$. 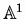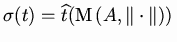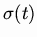This set $\sigma(t)$ satisfies a formula analogous to the spectral radius formula in the complex case. 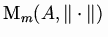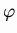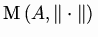We denote by $\mathscr{M}_m(A,\Vert\cdot\Vert)$ the set of the $\varphi$ in $\mathscr{M}(A,\Vert\cdot\Vert)$ whose kernel is a maximal ideal of A. 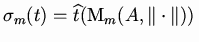We then put $\sigma_m(t)=\widehat t(\mathscr{M}_m(A,\Vert\cdot\Vert))$, and $s(t)=\{\lambda\in\Bbb K\mid t-\lambda \mbox{ non invertible} \}$. 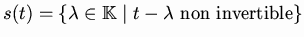We give a large condition on A, for these sets to satisfy the same kind of spectral radius formulæ. This is done by using holomorphic functional calculus with algebras of functions defined on compact subsets of $\Bbb A^1$. 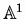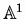In particular, we use a metric topology on $\Bbb A^1$thinner than the topology of pointwise convergence, but we show that both topologies have exactly the same connected sets, and also prove that connectedness is equivalent to arcwise connectedness.