Automatic Continuity of Basis Separating Maps¹

Lawrence Narici and Edward Beckenstein

Abstract:

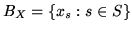
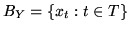
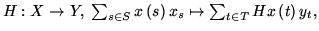
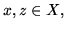
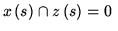
Let X and Y be non-Archimedean Banach spaces with bases $B_{X}=\left\{ x_{s}:s\in S\right\}$ and $B_{Y}=\left\{ x_{t}:t\in T\right\}$. 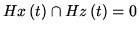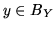We say that an additive map $H:X\rightarrow Y,\;\sum_{s\in S}x\left( s\right) x_{s}\mapsto \sum_{t\in T}Hx\left( t\right) y_{t},$ is basis separating with respect to B_X and B_Y if, for all $x,z\in X,$ $x\left( s\right) \cap z\left( s\right) =0\;$for all s implies $Hx\left( t\right) \cap Hz\left( t\right) =0$ for all t, we say that H is basis covering if for each $y\in B_{Y}$ there exists $x\in X$ 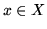such that Hx=y. We prove that a linear injective, basis covering mapH is automatically continuous. 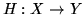We also deduce an open mapping theorem, namely that, with no continuity assumptions on H, a linear bijective basis separating map $H:X\rightarrow Y$ is a homeomorphism.