A characterisation of injective holomorphic functions in ultrametric analysis.

Juan Rivera-Letelier

J. Rivera-Letelier
Mathematics Department
SUNY at Stony Brook
Stony Brook, NY 11794-3660

rivera@math.sunysb.edu

Abstract:

We prove that a non constant holomorphic function f defined over an analytic subspace of $\mathbb{C} _p$ is injective if and only if

$$\left\vert \frac{f(x) - f(y)}{x - y} \right\vert^2 = \vert f'(x) \cdot f'(y)\vert, \mbox{ for every distincts $x$ and $y$}.$$

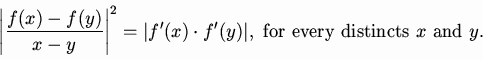
This characterisation proves the analogue, for holomorphic functions, of a conjecture of A. Escassut and M.C. Sarmant. On the other hand we give a counterexample to this conjecture, that concerns bi-analytic elements.

The proof is based on the fact that an holomorphic fucntion extends to (part of) p-adic hyperbolic space. The key property is that, when f is injective, this extension preserves the intrinsic distance of hyperbolic space.