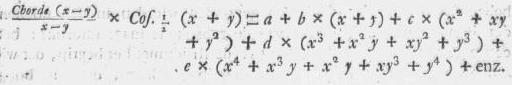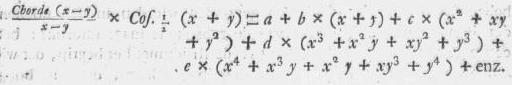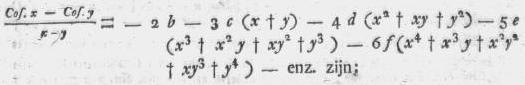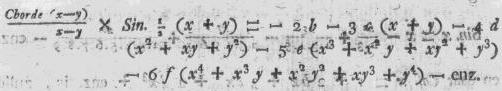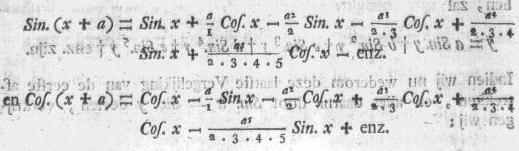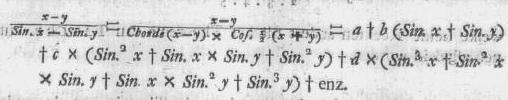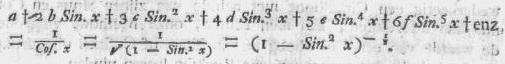VERHANDELING

OVER DE

R E E K S E N

DIENENDE OM DE RAPPORTEN VAN DE
CIRKELBOOGEN TOT DERZELVER SINUSSEN,
COSINUSSEN, TANGENTEN EN COTAN-
GENTEN WEDERKEERIGLIJK, UIT
EENVOUDIGE STELKUNSTIGE
BEGINSELEN, ZONDER BEHULP
DER DIFFERENTIAAL- OF
INTEGRAAL REKENING,
AFTELEIDEN.
DOOR

JACOB DE GELDER,

MATHEMATICUS

INGELEVERD AAN HET

BATAAFSCH GENOOTSCHAP

DER

PROEFONDERVINDELIJKE WIJSBEGEERTE

TE ROTTERDAM.


Aanvullende gegevens:
Artikel, verschenen in: Verhandelingen van het Bataafsch Genootschap der Proefondervindelijke Wijsbegeerte te Rotterdam XII (1798), pp. 241-268. In het origineel waren de noten alfabetisch genummerd, waarbij de nummering op de beide eerste pagina's doorliep, en vervolgens steeds opnieuw begon (vermoedelijk een vergissing van de zetter). In de HTML-versie is met cijfers gewoon doorgenummerd.


VERHANDELING

OVER DE

 R E E K S E N

 enz.
§. 1. Niemand, uitgenomen EULER en LA GRANGE, heeft zonder behulp der Differentiaal of Integraal Rekening de bekende Reeksen, die de Sinus, Cosinus, enz. van eenigen boog in eene functie van dien boog, en wederom omgekeerd eenigen boog in eene functie van zijnen sinus of cosinus, enz. weten te vinden: de Leerwijze, die deze twee groote Wiskunstenaars ingeslagen hebben, berust voor het grootste gedeelt op het zelfde beginsel; beiden hebben de Factoren van Sin2. x + Cos2. x = 1, die imaginaire grootheden zijn, ten grondlage hunner berekening gelegd. EULER (1) heeft van het oneindige gebruik gemaakt; maar LA GRANGE (2) heeft zijn betoog daar van bevrijdt, op een wijze, die zijn doordringend Analytisch oordeel zeer voordeelig kenmerkt: dan indien men, zonder hulp der imaginaire grootheden, door [pag. 242] eenvoudiger beginselen der Stelkunde tot het zelfde oogmerk geraaken kan, verdient zulk eene Leerwijze, om den grooteren graad van duidelijkheid, voorzeker den voorrang, en bevordert niet weinig den voortgang der Analytische kundigheden.

§. 2. Om dit Stuk zal ik aantoonen, hoe de eenvoudige beginselen der Driehoeksmeting en Stelkunde alleen voldoende zijn, om de rapporten van een boog tot zijnen Sinus, Cosinus, Tangent en Cotangent te kunnen uitdrukken: eene Methode aan de hand te geven, die tot dit oogmerk dienen kan, is in veele opzichten gewigtig (3); want behalven dat de beginsels der Differentiaal en Integraal Rekening door zulk een Methode als 't ware op de proef gesteld worden, verkrijgt men het voordeel om in eenen Cursus van de Driehoeksmeting den Leerlingen vroegtijdig bekend te maaken met waarheden en grondstellingen, die men anders genoodzaakt is, of zonder bewijs hun optegeeven, of dezelve geheel agterwege te laaten.

§. 3. Vooraf zal ik opmerken, dat een Cirkelboog langer dan zijne Chorde zijnde, de reden die de eerste tot het laatste heeft des te nader tot een reden van gelijkheid komt, naar evenredigheid de boog kleiner wordt, en op het oogenblik van de verdwijning des boogs in de reden van gelijkheid zelve verandert; dus zal Chorde x = x zijn, als x = 0 wordt; het zelfde heeft ook voor een boog en zijnen Sinus plaats; Sin. x = x, als x = 0 is, of wordt. Dit beginsel, dat algemeen bekend en in meest alle Elementaire Boeken der Meetkunde bewezen is, is eene der voornaamste beginselen, [pag. 243] waar op ons volgend betoog berusten zal en waar aan ik den Lezer vooraf wilde herinnerd hebben.

§. 4. Indien men de waarde van de Sinus eens boogs x door dezen boog x zal uitdrukken, moet deze uitdrukking van dien aart zijn, dat, voor eerst, deze uitdrukking van de Sinus gelijk 0 wordt, als x = 0 is, en ten tweede, dat dezelve voor elke waarde van x maar eene Sinus geeft, aangezien eenige boog maar eene bepaalde Sinus kan hebben.

§. 5. Om aan deze twee voorwaarden op de algemeenste wijze te voldoen, stel ik, Sin. x = ax + bx2 + cx3 + dx4 + ex5 + fx6 + enz., in welke uitdrukking a, b, c, d, e, f, enz. grootheden moeten zijn, die van alle combinaties van x bevrijdt zijn. -- De uitdrukking, die wij hier voor Sin. x aangenomen hebben, bevat alle mogelijke termen, die de natuur der zaake kan toelaaten, te weten alle geheele en stellige magten van x: negative of gebrokene magten van x zijn niet mogelijk; want in het eerste geval zou, indien x = 0 gesteld wierd, de Sinus van 0 oneindig groot worden; terwijl in het tweede geval de Sinus eens boogs zoo veele verschillende waardijen hebben zou, als 'er éénheden gevonden wierden in den noemer der breuk, die de exponent van de gebrokene magt uitdrukt: het eerste geval is niet mogelijk, het tweede strijdt met het begrip, dat wij aan het woord Sinus hegten, welk begrip ons leert, dat eene boog maar eene Sinus kan hebben: als dan eene uitdrukking voor Sinus x zal ontwikkeld worden, kunnen de termen dezer ontwikkelde uitdrukking geene andere dan geheele en stellige magten van x inhouden; dan hoedanige en welke deze ontwikkelde magten zijn, zullen wij nu door de volgende Analysis bepaalen.

§. 6. Als dan
Sin. x = ax + bx2 + cx3 + dx4 + ex5 + fx6 + enz. is, zal, aangezien de Coëfficienten a, b, c, d, e enz. in geenen deele [pag. 244] van x afhangen, maar op zigzelve standvastige grootheden blijven,
Sin. y = ay + by2 + cy3 + dy4 + ey5 + fy6 + enz. zijn.
Indien wij nu deze laatste uitdrukking van de eerste aftrekken, verkrijgen wij:
Sin. x - Sin. y = a × (x - y) + b × (x2 - y2) + c × (x3 - y3) + d × (x4 - y4) + e × (x5 - y5) + f × (x6 - y6) + enz.
Maar aangezien Sin. x - Sin. y = 2 Sin. ½(x - y) × Cos. ½(x + y) = Chorde (x - y) × Cos. (½x + ½y)
zal men hebben:
Chorde (x - y) × Cos. ½(x + y) = a × (x - y) + b × (x2 - y2) + c × (x3 - y3) + enz.
en deelende nu beide de leden dezer Vergelijking door x - y, zal men wederom deze nieuwe uitdrukking verkrijgen:
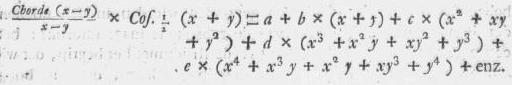Als wij nu in deze uitdrukking x = y stellen, wordt de reden van Chorde (x - y) tot x - y eene reden van gelijkheid, of liever Chorde (x - y) : x - y = 1 : 1; gevolgelijk [Chorde (x - y)]/[x - y] = 1, en Cos. ½(x + y) = Cos. x en derhalven verandert de laatste Vergelijking in de volgende:
Cos. x = a + 2bx + 3cx2 + 4dx3 + 5ex4 + 6fx5 + 7gx6 + enz. [pag. 245]
Als nu in deze laatste uitdrukking x = 0 gesteld wordt, verkrijgen wij Cos. 0° = a; maar daar de Cosinus van 0° gelijk de Radius is, en wij de Radius = 1 stellen, zoo blijkt hier uit dat a = 1 moet genomen worden, en nu weten wij, dat indien
Sin. x = x + bx2 + cx3 + dx4 + ex5 + fx6 + gx7 + enz. gesteld wordt, de waarde van de Cosinus dezes zelfden boogs zal uitgedrukt worden door
Cos. x = 1 + 2bx + 3cx2 + 4dx3 + 5ex4 + 6fx5 + 7gx6 + enz.

§. 7. Indien men deze beide uitdrukkingen voor Sinus x en Cosinus x met elkander vergelijkt, ziet men duidelijk, dat beide uitdrukkingen van elkander afhangen, en dat deze onderlinge afhangelijkheid daar in bestaat, dat de Coëfficienten der termen van de ontwikkelde uitdrukking voor de Cosinus, van die der termen van de Reeks, de waarde van de Sinus uitdrukkende, volgens eene onveranderlijke wet van elkander afhangen.

§. 8. Wij zouden nu door de bekende Formula Sin2.x + Cos2.x = 1 of door Sin. 2x = 2 Sin. x × Cos. x (4) of wel door eenige andere [pag. 246] uitdrukking de waarde der Coëfficienten b, c, d, e, enz. kunnen bepaalen, en de eerste dezer Formulas zoude daartoe wel de geschiktste zijn; maar wij kunnen eenen korteren en veel cierlijkeren weg inslaan, en die tevens meer met den geest onzer Leerwijze overéénkomt, door namelijk uit de gevondene Reeks voor de waarde van de Cosinus wederkeerig de uitdrukking voor de waarde des Sinus afteleiden, het welk ons twee identieke waardijen voor Sinus x geeven zal, uit vergelijking van welker eveneens geplaatste Coëfficienten met elkander de waardijen der Coëfficienten b, c, d, e, enz. zullen bekend worden.

§. 9. Wij hebben gevonden, dat
Cos. x = 1 + 2bx + 3cx2 + 4dx3 + 5ex4 + 6fx5 + 7gx6 + enz.
Maar nu zal ook
Cos. y = 1 + 2by + 3cy2 + 4dy3 + 5ey4 + 6fy5 + 7gy6 + enz.
trekkende nu de onderste vergelijking van de bovenste, hebben wij:
Cos. x - Cos. y = 2b × (x - y) + 3c(x2 - y2) + 4d(x3- y3) + 5e(x4- y4) + 6f(x5 - y5) + 7g(x6 - y6) + enz.
Deelende nu deze laatste vergelijking door x - y, zal, aangezien het verschil van twee bogen negatief is, indien het verschil hunner Cosinussen positief genomen wordt,
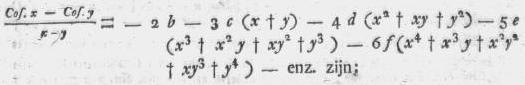maar nu is Cos. x - Cos. y = 2 Sin. ½(x - y) × Sin. ½ (x + y) = Chorde (x - y) × Sin. ½ (x + y) (5). [pag. 247] en gevolgelijk
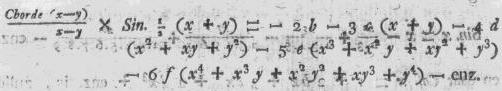Indien wij nu in deze laatste Vergelijking x = y stellen, wordt om de bovenbijgebragte reden (§. 3.) Sin. ½(x + y) = Sin. x en [Chorde (x - y)]/[x - y] = 1/1 = +1. en de geheele laatste Vergelijking verandert in deze:
Sin.x = -2b - 2 × 3. cx - 3 × 4. dx2 - 4 × 5. ex3 - 5 × 6. fx4 - 6 × 7. gx5 - 7 × 8. hx6 - 8 × 9. ix7 - enz.

§. 10. Deze laatste uitdrukking moet identicé dezelfde zijn als de aangenomene uitdrukking
Sin. x = ax + bx2 + cx3 + dx4 + ex5 + fx6 gx7+ enz. ; en gevolgelijk moeten de Coëfficienten der magten, welke dezelfde exponenten hebben, in beide uitdrukkingen aan elkander gelijk zijn, en indien wij deze nu daadelijk onderling vergelijken, verkrijgen wij:
b = 0
c = - 1/(2.3)
d = 0
e = -c/(4.5) = + 1 / (2.3.4.5)
f = 0
g = -e/(6.7) = - 1 / (2.3.4.5.6.7)
h = 0
i = -g/(8.9) = + 1 / (2.3.4.5.6.7.8.9)
enz. . . . . enz. . . . . [pag. 248]
Wij hebben dus voor de Sinus van een boog de volgende uitdrukking:
Sin. x = x - x3/(2.3) + x5/(2.3.4.5) - x7/(2.3.4.5.6.7) + x9/(2.3.4.5.6.7.8.9) - enz.
en daar Cos. x = 1 + 2bx + 3cx2 + 4dx3 + enz. is, zullen de gevondene waardijen van b, c, d, e, f, enz. in dezelve gesubstitueerd zijnde, voor de waarde van de Cosinus deze uitdrukking geeven:
Cos. x = 1 - x2/(2) + x4/(2.3.4) - x6/(2.3.4.5.6) + x8/(2.3.4.5.6.7.8) - enz.
Zijnde deze dezelfde Reeksen, welke bij de Schrijvers, met behulp der Differentiaal- of Integraal Rekening bepaald worden.

§. 11. Geene dezer twee Reeksen kunnen ergens ophouden; maar dezelve gaan tot in het oneindige voort, gelijk uit de berekening van zelve blijkt, ook ziet men met een' opslag van het oog, dat beide Reeksen, volgens eene standvastige wet afloopen, welke bij het oppervlakkig inzien van zelve in het oog loopt; ook ziet men dat een minder aantal termen des te naauwkeuriger de waarde van de Sinus of Cosinus uitdrukt, naarmaate de boog, voor welke men de Sinus of Cosinus berekend, kleiner is.

§. 12. Uit deze twee gevondene Reeksen, de Sinus en Cosinus van een boog uitdrukkende, kan men twee andere Reeksen afleiden, waar door Sin. (x + a) en Cos. (x + a) beiden in Reeksen, naar de afmeetingen van a geordend, kan uitdrukken, want
en Sin. (x + a) = Sin. x × Cos. a + Cos. x × Sin. a
en Cos. (x + a) = Cos. x × Cos. a - Sin. x × Sin. a zijnde, substitueert men in beide deze vergelijkingen
voor Sin. a = a - a3/(2.3) + a5/(2.3.4.5) - enz. en voor Cos. a = 1 - a2/2 + a4/(2.3.4) - enz. [pag. 249]
en wij verkrijgen
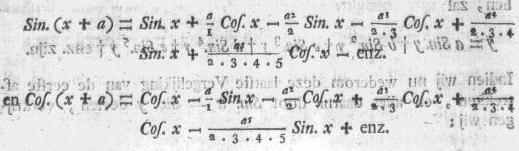welke beide Reeksen anders uit het Theorema van TAYLOR kunnen afgeleid worden.

§. 13. Niettegenstaande men door de Theorie van de wederkeering der Reeksen uit de gevondene waarde van Sin. x en Cos. x, wederkeerig een Cirkelboog met behulp van zijnen Sinus en Cosinus kan uitdrukken, kan men echter, onze Methode volgende, de waarde van een Cirkelboog in zijn Zinus of Cosinus uitgedrukt, zonder behulp der eerstgevondene Reeksen leeren vinden.

§. 14. Stellende dan x eenigen boog van een Cirkel beteekent, dan zal de waarde van x in Sinus x uitgedrukt, noodwenig tot deze gedaante behooren.

x = a. Sin. x + b. Sin.2 x + c. Sin.3 x + d. Sin.4 x + e. Sin.5 x + enz.

want 'er kunnen geene negative magten plaats hebben, dewijl anders, als Sin. x = 0 wierde, x = [oneindig] zoude zijn. -- Ook kunnen er geene termen met gebrokene magten van x aangedaan in voorkomen, dewijl 'er anders imaginaire boogen voor eenen wezenlijken Sinus zouden kunnen plaats hebben, iets dat volstrekt onmogelijk is: voor het overige isde uitdrukking volkomen voldoende, want als wij Sin. x = 0 stellen, wordt x insgelijks = 0; en daar de [pag. 250] Coëfficienten a, b, c, d, e, enz. met Sin. x niets gemeens hebben, zal

y = a. Sin. y + b. Sin.2 y + c. Sin.3 y + d. Sin.4 y + e. Sin.5 y + enz.

Indien wij nu wederom deze laatste Vergelijking van de eerste aftrekken, en alles daarna door Sin. x - Sin. y deelen, verkrijgen wij:
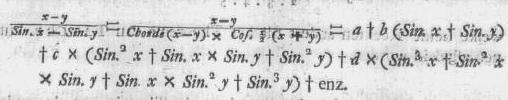Stellende nu vervolgens, dat x = y zij, zal
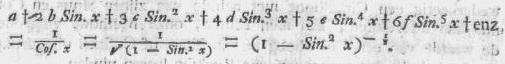Indien wij nu verder de uitdrukking (1 - Sin.2 x)-½ volgens het Theorema van NEWTON ontwikkelen, hebben wij:


Voetnoten:

(1) EULER, Introd. ad Anal. Infin. Pars I. pag. 98 & seq.

(2) LA GRANGE, Theorie des fonctions Analyt. §. 25. pag. 24. Ook verdient DE PRONY, in N° 2. van het Journal Polytechnique, pag. 14 &c. nagezien te worden.

(3) L'HUILIER HEEFT IN DE Philosophical Transact. of the Royal Sociey of London 1796. Part. I. pag. 142, dit zelfde onderwerp voortreffelijk behandeld; maar daar hij ook van de imaginaire grootheden gebruik maakt, zie pag. 161, als mede van het denkbeeld der 1°. en 2°. enz. Differentien, meene ik, dat de Methode, welke ik in dit Stukje zal voordraagen, eenvoudiger en meer rechtstreeks dan de zijne is.

(4) Men kan uit de Formula Sin. 2x = 2 Sin.x × Cos. x, de Reeks voor Sin. x in waarde van x berekenen: want Sin. 2x = 2 Sin. x × Cos. x = 2 Sin. x (1 - Sin.2 x)+½, welke laatste uitdrukking, door het Binomium van NEWTON ontwikkeld zijnde, geeven zal:
Sin. 2x = 2 Sin.x - Sin.3x - 3/4Sin.5x - 3/4.5/6Sin.7x - 3/4.5/6.7/8Sin.9x - enz. (A). Indien wij nu aannemen, dat Sin. x = ax + bx2 + cx3 + dx4 + enz. zal Sin. 2x = 2ax + 4bx2 + 8cx3 + 16dx4 + enz. zijn: zal men de magten van Sin. x in de orde van de Reeks ax = bx2 enz. berekenende, en deze magten in de Reeks (A) substitueerende, eene Reeks voor Sin. 2x verkrijgen, die identicé dezelve zal zijn met Sin. 2x = 2ax + 4bx2 + enz.: de Coëfficienten van de gelijke magten dezer identieke uitdrukkingen met elkander vergelijkende, verkrijgt men zoo veele vergelijkingen als 'er termen zijn, met welker hulp de Coëfficienten a, b, c, d enz. bepaald worden, uitgenomen a; want men vindt, Sin. x = ax - (ax3)/(2.3) + (ax5)/(2.3.4.5) - (ax7)/(2.3.4.5.6.7) + enz., in welke a = 1 moet zijn, het gene LA GRANGE in zijne Traité des Fonctions Analytiques betoogd heeft. Zie pag. 20.

(5) CAGNOLI, Trigonometrie, §. 85.

(6) Zulks kan ook nog uit andere beginselen afgeleid worden, zoo als ik hier in 't kort zal aantoonen: indien men de formula Tang. 2x = [2 Tang. x]/[1 - Tang.2 x] in eene Reeks ontwikkelt, met behulp van de divisie, verkrijgt men:
Tang. 2x = 2 Tang. x + 2 Tang. 3x + 2 Tang. 5x + 2 Tang. 7x + enz.
Stellende nu Tang. x = x + bx2 + cx3 + enz. kan men de waarden van Tang. 3x, Tang. 5x, enz. berekenen, en in de Reeks van Tang. 2x = 2 Tang. x + 2 Tang. 3x + enz. substitueeren; daar nu Tang. 2x = 2x + 4bx2 + 8cx3 + enz. is, zullen de Coëfficienten der termen van gelijke magten met elkander vergeleken zijnde, de Coëfficienten van de termen der aangenomene Reeks doen bekend worden.