Wat gaat er mis?
De nieuwste trend in het wiskundeonderwijs is realistische wiskunde. Ik heb al betoogd dat wiskunde bij uitstek abstract is. Wiskunde is niet realistisch. Realistische wiskunde bestaat niet. Met zoiets bereik je niks, evenmin als met abstract voetballen.
Natuurlijk ligt de kracht van de wiskunde in haar relatie met de realiteit: de realiteit van de wereld om ons heen en de realiteit in de zin van natuur en techniek. Maar het onderscheid moet wel blijven bestaan. Anders verdwijnt de wiskunde omdat dan het exact redeneren is afgeschaft.
Laten we eens terugkeren naar de Stelling van Pythagoras. Dat is dus een stelling en geen natuurwet. Je stelt hem dus niet op experimentele wijze vast zoals de bewegingswetten van Newton. Het is een resultaat van een redenering. Hoe wordt de Stelling van Pythagoras op school behandeld? Bij enkele methodes voor wiskundeonderwijs heb ik dit opgezocht. Mijn interesse gaat daarbij vooral uit naar het deductieve aspect. Het gaat niet om een onderzoek: ik geef hier slechts mijn ervaringen.
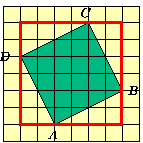
De grote educatieve uitgeverij Wolters-Noordhoff brengt meerdere methodes voor het wiskundeonderwijs op de markt. Een van deze methodes is Netwerk, een uitgave met vele gekleurde plaatjes en tekeningen. De Stelling van Pythagoras wordt behandeld in deel twee voor HAVO en VWO. In een paragraaf getiteld Oppervlakten, die vooraf gaat aan de paragraaf met titel De Stelling van Pythagoras, wordt geoefend in het berekenen van oppervlakten van op ruitjespapier getekende vierkanten die scheef in dit rooster van ruitjes liggen.
Berekenen van Oppervlakten in Netwerk
Hoe bereken je de oppervlakte van een vierkant dat scheef in een rooster
ligt?
|
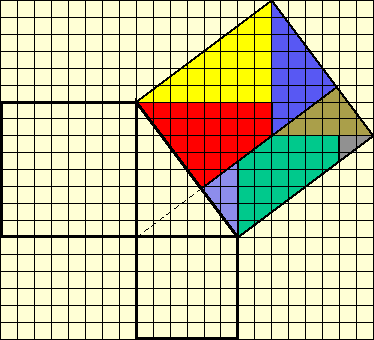
Ik had het al eerder over wiskunde als receptenboek. Als U zich herinnert hoe de Stelling van Pythagoras bewezen kan worden, dan zou U zich ook kunnen indenken dat dit een uitstekende voorbereiding is op een bewijs dat op deze manier niet uit de lucht komt vallen: pas dit recept toe op een willekeurige rechthoekige driehoek en je krijgt de Stelling van Pythagoras. In de paragraaf over deze stelling wordt dit rekenwerk in een opgave herhaald met de drie vierkanten die op de zijden staan van een rechthoekige driehoek met rechthoekszijden 2 en 5. Deze oppervlakten zijn dan 4, 25 en 29. Nog steeds een ogenschijnlijk goed doordachte voorbereiding op de Stelling van Pythagoras. Dan wordt de stelling geformuleerd. Je slaat de bladzijde om en ...geen bewijs, alleen rekenvoorbeelden. Je kijkt nog een bladzijde verder. In een opgave staat een ongewoon ingewikkelde veelkleurige figuur opgebouwd uit driehoeken, vierhoeken en vijfhoeken. Deze figuur moet je overtekenen. De drie-, vier- en vijfhoeken uitknippen en met deze figuren een legpuzzel oplossen. Ten slotte wordt je gevraagd wat je eigenlijk hebt aangetoond. De leerling zal wel denken dat dit nu hogere wiskunde is, daarin versterkt door de opmerking die daarna onder aan de bladzijde staat en die gaat over het begrip bewijs.
Opgave uit Netwerk
|
Vervolgens wordt er uitvoerig ingegaan op het gebruik van de stelling.
Eveneens van Wolters-Noordhoff is de methode Moderne wiskunde. De Stelling van Pythagoras staat in deel 2 voor MAVO, HAVO en VWO. Het is een uitgave in tweekleurendruk. Dat geeft hoop. Ook hier voorbereidend werk met scheef gesitueerde vierkanten. Hier wordt de Stelling pas een stelling nadat hij in vijf gevallen is nagerekend in plaats van in één geval. Verder moet gezegd worden dat er in de vorm van een opgave aandacht wordt geschonken aan het algemene geval, zij het op een te suggestieve wijze: van een hoek wordt zonder omwegen aangenomen dat hij recht is. Vanuit wiskundig standpunt is deze methode dus beduidend beter: er is aandacht voor het algemene geval. Wel wordt het bewijs weggestopt in een opgave.
Op een klein aantal scholen wordt De Wageningse Methode gebruikt. Hij is ontwikkeld door leraren met een Nijmeegse achtergrond en wordt tegenwoordig op een niet-commerciële basis uitgegeven. Ook hier zijn er voorbereidende oefeningen met het berekenen van oppervlakten. Hier wordt gerekend aan vier rechthoekige driehoeken. Belangrijk is dat de Stelling pas een stelling is als hij bewezen is. Het bewijs maakt deel uit van de leerstof: het staat gewoon in de tekst. Wel wordt ook hier het recht zijn van een hoek onder tafel gewerkt. Aan het gebruik van de stelling wordt overigens niet minder aandacht geschonken dan hetgeen bij Netwerk het geval is.
De methode Netwerk is niet bijzonder in zijn soort. Dat ik deze er uit haal is nogal toevallig. De schrijvers van Netwerk valt niets te verwijten: het is een uitwerking van de doelstellingen van de basisvorming. Toch zijn methodes als Netwerk een ramp voor het ontwikkelen van wiskundig inzicht. Bij de methode Moderne wiskunde is er, zonder gerichte prikkels van de kant van de leraar, te weinig uitdaging voor goede leerlingen. De Wageningse Methode heeft voor de wiskunde het hart op de juiste plaats, al valt er wiskundig nog wel wat te verbeteren: de tijdgeest laat ook hier zijn sporen na.
De stelling die zegt dat de som van de hoeken van een driehoek 180° is, ligt ten grondslag aan het bewijs van de Stelling van Pythagoras. Deze logische samenhang wordt in de leerboeken niet op prijs gesteld. In Netwerk wordt deze stelling niet geformuleerd, maar is weggestopt in een `verdiepingsopgave' in deel 1. Die opgave gaat trouwens over Sander die na het avondeten de hond moet uitlaten. In de Methode Realistische wiskunde, uitgegeven door Malmberg, wordt de stelling over de hoeken van een driehoek bewezen met tekenen, knippen, scheuren en plakken. Het gaat daar dus om een natuurwet. Het kan gewoon niet realistischer. Het argument voor de stelling is drie bladzijden eerder al aan de orde geweest. Liever knippen en plakken dan logica.
Vroeger-toen ik op school zat-werd de Stelling van Pythagoras meestal als volgt bewezen:
Bewijs van de Stelling van Pythagoras
ofwel,
Dus
|
Dit bewijs maakt geen gebruik van het begrip oppervlakte, omdat het zo als wiskundig strenger werd ervaren. Oppervlakte werd dan later ingevoerd. Ik zat op een Amsterdamse lagere school waar het niet gebruikelijk was leerlingen door te verwijzen naar het middelbaar onderwijs dat op de universiteit voorbereidde. Ik was de enige in mijn klas die naar zo'n school ging: de Tweede Openbare Handelsschool (een categorale HBS-A), omdat ik teveel moeite met wiskunde zou hebben. Ik kreeg daar les van de heer Peters die de gehele meetkunde die je je eigen moest maken op bord schreef en die je dan kon overnemen in een schrift. Ziehier de hier relevante bladzijde en bedenk dat het een Handelsschool betrof:
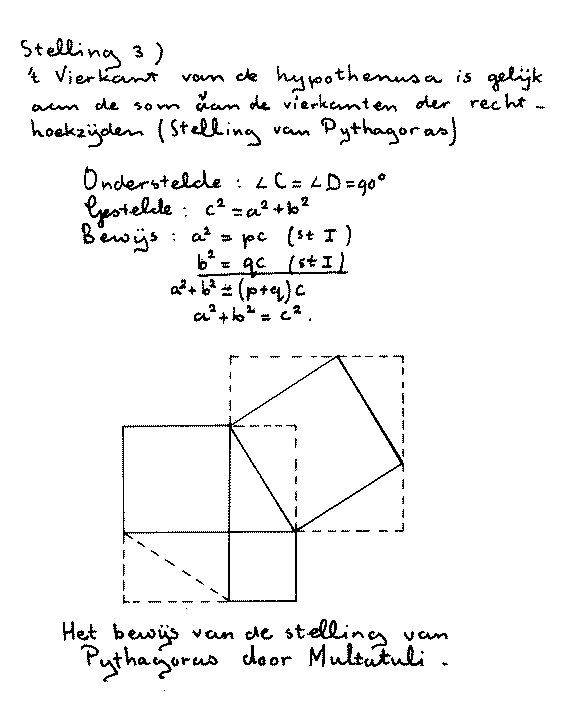
|
De docent kon het niet laten als toegift het bewijs van Multatuli te vermelden. Dit bewijs lijkt op wat ik al eerder toonde, alleen de algebra is nog meer uitgebannen. Algebra is niet populair in het onderwijs.
Het niveau van redeneren in de wiskunde heeft in de Griekse oudheid een grote sprong voorwaarts gemaakt. Eeuwen lang zijn wiskundelessen op scholen erop gebaseerd geweest en terecht. Ik zeg niet dat dat daarom dan ook goede lessen waren. Goede wiskunde kan gepaard gaan met een slechte didactiek. En dat was misschien meer regel dan uitzondering. Waar ik mij tegen verzet is de idee dat goede wiskunde slechte didactiek ís. We weten inmiddels dat ook de Babyloniërs gevoel hadden voor wiskunde. Zij deden iets dat we nu wiskunde zouden noemen. De sprong vooruit van de Grieken, die hadden zij niet genomen. In de realistische wiskunde wordt deze sprong genegeerd. Met zulke wiskunde wordt het nooit wat, hoeveel didactici er ook van gecharmeerd zijn.
Een andere sprong voorwaarts in de geschiedenis van de wiskunde is in de vorige eeuw gemaakt. Ik doel hier op het toen ontstane inzicht in de reële getallen. Dit inzicht is cruciaal bij alles wat met limieten te maken heeft. En dat is veel. Denk aan continuïteit, differentiëren, integreren, differentiaalvergelijkingen, kansrekening, statistiek, fractals, chaos en nog veel meer: wiskunde die ten grondslag ligt aan onze gehele moderne technologie. Wat doen we op school? Omdat we moeilijkheden willen omzeilen, gaan we moeilijk doen over fundamentele begrippen. Weinig leerlingen die het echt begrijpen. Omdat velen het te moeilijk vinden is er vervolgens de tendens om nog meer onder het kleed te vegen.
Als iets zo belangrijk is, dat, als je het goed begrijpt, je opeens nog veel meer kunt gaan begrijpen, dan moet daar extra tijd aan besteed worden. Dat mag best ten koste gaan van wat allerlei wiskundegebruikers als noodzakelijk en onmisbaar zien. Waarom moet ieder kind de moderne wiskunde leren op het niveau van een Babyloniër? Welk doel is daarmee gediend?
Wat over reële getallen in schoolboeken staat is bedroevend. In Netwerk bijvoorbeeld vond ik niet meer dan de volgende definitie: een komma-getal is een getal met een komma er in. De noodzaak om met andere getallen dan breuken te rekenen ontstaat als we gaan worteltrekken. De schoolboeken komen niet verder dan soms op te merken dat ze met benaderingen werken. Dat √2 irrationaal is, is niet realistisch en wordt derhalve niet onderwezen. Voor de Grieken was het een schok, maar dat was hun probleem.
Wat is er volgens mij nu echt mis met veel van ons wiskundeonderwijs? De meest diepgaande fout is het verwarren van abstractie en realiteit. Abstractie is ontstaan uit de behoefte tot helderheid. In de hersenspinsels van de wiskunde is er sprake van absolute helderheid. In ons onderwijs wordt dat mistig gemaakt en dat is zonde. Het is een gemiste kans voor het leren van exact denken.
In het onderwijs gaat het verrassend weinig over getallen. Begrippen die een kind kan begrijpen worden niet behandeld, mogelijk omdat ze te weinig realistisch zijn. De meetkunde heeft het wat dat betreft gemakkelijker, maar daarmee loopt deze wel het gevaar door een realistische aanpak als natuurwetenschap te worden behandeld.
Maar het kan erger. De techniek staat voor niets. We kunnen nu de grafische rekenmachine gaan gebruiken in het onderwijs. Functies als de sinus krijg je in de vorm van een grafiek op een schermpje. Door waarnemen kun je nu eigenschappen aan de grafiek aflezen. Je kunt op het scherm zien dat bijvoorbeeld de som van de kwadraten van de sinus en de cosinus gelijk is aan 1. Je hoeft dan niet te begrijpen wat de sinus en de cosinus zijn en ook niet dat het hier om de Stelling van Pythagoras gaat. Zo'n grafische rekenmachine is een doos met knoppen. Heel handig voor het doen van berekeningen. In de handen van sommigen kan het in het onderwijs ingezet gaan worden om de wiskunde om zeep te helpen. Die is dan pas echt naar de knoppen. Onze hersenspinsels zijn dan niet in eerste instantie gericht op het beheersen van de realiteit,maar op het beheersen van deze doos met knoppen. En daar horen geheel andere hersenspinsels bij.
Op wiskundig gebied gaat tegenwoordig de computeralgebra het verst in het uit handen nemen van wiskundige activiteit. In de wiskunde gaat het om exactheid. Soms willen we een benadering van bijvoorbeeld √2 met een aantal decimalen. Vaak willen we het exacte getal hebben en daar verder mee redeneren. Computeralgebra-pakketen kunnen met de exacte dingen rekenen en ook met onbekenden, die we vaak met x aanduiden. Alles wat wiskundigen aan algoritmen, berekeningsmethoden bedacht hebben maakt deel uit van deze software. Sterker nog: nu deze mogelijkheden er zijn bedenken we steeds slimmere rekenmethoden die we hierin kunnen implementeren. Veel wiskundig onderzoek heeft zo tot resultaat dat het anderen mogelijk maakt om op domme wijze met wiskunde om te gaan. Wiskunde is niet algoritmisch van aard. Zelfs als men alleen in algoritmen is geïnteresseerd, dan is het nog steeds zo dat er geen algoritmen zijn om algoritmen te bedenken. We hebben nu fraaie uiterst krachtige wiskundige knoppendozen als Mathematica en Maple. Deze zijn bijzonder nuttig voor het toepassen van wiskunde en voor het doen van berekeningen in de wiskunde waar we als eenvoudig sterveling anders niet toe zouden komen. Door zulke berekeningen kunnen we trouwens soms ook ons inzicht vergroten. Het gebruik ervan kan ik van harte aanbevelen. Dat ze in het VWO nog weinig worden gebruikt komt door de prijs. Dat is maar goed ook, want ze bieden een veelheid aan mogelijkheden om de ontwikkeling van wiskundig inzicht bij leerlingen tegen te gaan.
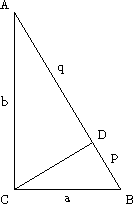 Neem D zo dat CD loodrecht op AB. Dan zijn ∆ABC, ∆CBD en ∆ACD gelijkvormig. Dus
Neem D zo dat CD loodrecht op AB. Dan zijn ∆ABC, ∆CBD en ∆ACD gelijkvormig. Dus