Je voert een toets uit om te onderzoeken of een gevonden
verschil op toeval berust of dat er écht een verschil bestaat
tussen de twee steekproeven. Om deze beslissing te maken, of je
wel of niet de nulhypothese verwerpt, gebruik je de
toetsingsgrootheid en/of de overschrijdingskans van de
toetsingsgrootheid. Als de overschrijdingskans kleiner is dan het
significantieniveau dat je hanteert moet je de nulhypothese
verwerpen.
Voorbeelden:
 |
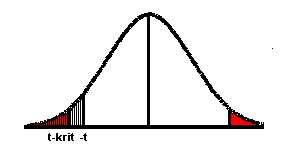
Stel je hebt een t-toets gedaan en je vindt t=-1,5 en de kritische waarde van t (tkrit) is 2, dan ziet het plaatje met de kansverdeling er uit als hiernaast. De rode vlakken representeren ieder ˝a. Het gearceerde gedeelde van de grafiek (links van t) geeft de overschrijdingskans aan: de kans dat je als de nulhypothese waar is een t waarde vindt die kleiner is dan -1,5. In dit geval is p>˝a, dus wordt de nulhypothese geaccepteerd. Je kan ook kijken naar t, t>tkrit dus wordt de nulhypothese niet verworpen (bij positieve geldt dat je de nulhypothese juist verwerpt als t>tkrit). | |
 |
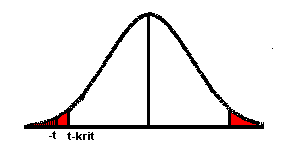
Stel dat je weer een t-toets hebt gedaan en je vindt t=-2,5 en de kritische waarde van t (tkrit) is 2, dan ziet het plaatje met de kansverdeling er uit als hiernaast. De rode vlakken representeren ieder ˝a. Het gearceerde gedeelde van de grafiek (links van t) geeft de overschrijdingskans aan: de kans dat je als de nulhypothese waar is een t waarde vindt die kleiner is dan -2,5. In dit geval is p<˝a, dus wordt de nulhypothese verworpen. In dit geval is t<tkrit dus nulhypothese verwerpen (als er een positieve t was gevonden geldt dat je de nulhypothese verwerpt als t>tkrit). |