Analytic mappings in the tree
Mult(K[x]).
Kamal Boussaf, Alain Escassut, and
Nicolas Maïnetti
Abstract Let K be an algebraically closed complete ultrametric field, let
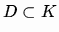 be closed and
bounded, and let H(D) be the Banach K-algebra of analytic elements on D. Let
Mult(K[x]) (resp.
be closed and
bounded, and let H(D) be the Banach K-algebra of analytic elements on D. Let
Mult(K[x]) (resp.
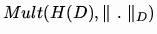 )
be the set of multiplicative semi-norms on K[x]) (resp. of continuous multiplicative semi-norms on H(D))
which are known to be characterized by circular filters.
Mult(K[x]) is provided with the topology of simple convergence,
and with a metric topology based upon a tree structure for which it is complete. Given a bounded closed infraconnected set
)
be the set of multiplicative semi-norms on K[x]) (resp. of continuous multiplicative semi-norms on H(D))
which are known to be characterized by circular filters.
Mult(K[x]) is provided with the topology of simple convergence,
and with a metric topology based upon a tree structure for which it is complete. Given a bounded closed infraconnected set
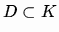 ,
the boundary of
,
the boundary of
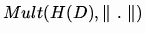 inside
Mult(K[x]) with respect to the topology of simple convergence, is equal to the
Shilov boundary for
inside
Mult(K[x]) with respect to the topology of simple convergence, is equal to the
Shilov boundary for
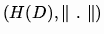 .
If D is affinoid (particularly), this is also the boundary of
.
If D is affinoid (particularly), this is also the boundary of
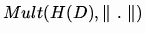 inside
Mult(K[x]) with respect to the metric topology. We show that every element
inside
Mult(K[x]) with respect to the metric topology. We show that every element
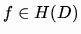 has continuation to a mapping f* from
has continuation to a mapping f* from
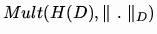 to
Mult(K[x]) which is
continuous for both topologies and uniformly continuous for the metric topology. The family of functions
to
Mult(K[x]) which is
continuous for both topologies and uniformly continuous for the metric topology. The family of functions
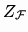 from
H(D) to
Mult(K[x]) defined as
from
H(D) to
Mult(K[x]) defined as
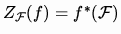 (where
(where 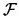 is a circular filter secant with D) is
uniformly equicontinuous with respect to the metric topology. If the field K is separable, f*
is uniformly continuous for both topologies. Results
also apply to meromorphic functions in K. A meromorphic function in K defines an increasing function f* (with respect
to the order of
Mult(K[x])) if and only if it is an entire function.
In a Krasner-Tate algebra
is a circular filter secant with D) is
uniformly equicontinuous with respect to the metric topology. If the field K is separable, f*
is uniformly continuous for both topologies. Results
also apply to meromorphic functions in K. A meromorphic function in K defines an increasing function f* (with respect
to the order of
Mult(K[x])) if and only if it is an entire function.
In a Krasner-Tate algebra
![$H(D)=K\{t\}[x]$](img9.gif) ,
where
,
where
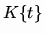 is a topologically pure extension of dimension 1 and x is the identical function on D integral over
is a topologically pure extension of dimension 1 and x is the identical function on D integral over 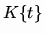 ,
we can precisely show that the Gauss norm on
,
we can precisely show that the Gauss norm on 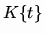 admits a number of extensions to
admits a number of extensions to ![$K\{t\}[x]$](img11.gif) which is equal to
the cardinal of the Shilov boundary of
which is equal to
the cardinal of the Shilov boundary of
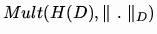 .
.
AMS Classification: 46S10, 12J25, 12J27