Strict Topologies and Vector-Measures on non-Archimedean Spaces
A. K. KATSARAS
University of Ioannina, Greece
Abstract
,5cm
Let
Cb(X,E) be the space of all bounded continuous functions from a
zero-dimensional
Hausdorff topological space X to a non-Archimedean Hausdorff locally
convex space E.
In this paper, we study several of the properties of the strict topologies
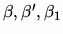 and
and
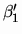 on
Cb(X,E) and we show that the
corresponding dual spaces
are certain subspaces of a space M(X,E') of finitely-additive
E'-valued measures on the
algebra of all clopen subsets of X. In case E is polar, it is proved
that the topology
on
Cb(X,E) and we show that the
corresponding dual spaces
are certain subspaces of a space M(X,E') of finitely-additive
E'-valued measures on the
algebra of all clopen subsets of X. In case E is polar, it is proved
that the topology
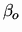 coincides with the polar topology associated with
coincides with the polar topology associated with  .
Also two new
topologies
.
Also two new
topologies 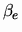 and
and
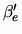 on
Cb(X,E) are introduced.
These topologies are
defined as inductive topologies by using the family of all continuous
ultra-pseudometrics
on X. Some of the properties of these topologies are investigated. When
E is metrizable,
it is shown that
on
Cb(X,E) are introduced.
These topologies are
defined as inductive topologies by using the family of all continuous
ultra-pseudometrics
on X. Some of the properties of these topologies are investigated. When
E is metrizable,
it is shown that 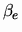 is coarser than
is coarser than 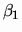 and coincides with
the topology
of simple convergence on uniformly-bounded equicontinuous subsets of
Cb(X,E). In the
same case, it is proved that
and coincides with
the topology
of simple convergence on uniformly-bounded equicontinuous subsets of
Cb(X,E). In the
same case, it is proved that
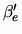 yields as dual space the space
of the so
called separable members of M(X,E').
yields as dual space the space
of the so
called separable members of M(X,E').