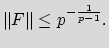Analytic roots of a rational function
Marie-Claude SARMANT
Let
D = d ( 0,1-) be the open unit disk of
 ,
let A(D) be the set of analytic functions in D and let
,
let A(D) be the set of analytic functions in D and let
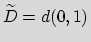 be the unit disk ofK. If there exist
be the unit disk ofK. If there exist
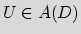 with U(0) =0 and
with U(0) =0 and
![$ P \in K[x]$](img4.gif) with P(0)=0, such that
with P(0)=0, such that
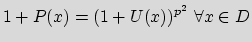 ,
then
,
then
 is the absolute value of at least two coefficients of P.
Consequently we can prove a conjecture asked by Escasssut, assuming an
additive condition: Let
is the absolute value of at least two coefficients of P.
Consequently we can prove a conjecture asked by Escasssut, assuming an
additive condition: Let
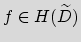 be such that the differential
equation y' = fy has a solution
be such that the differential
equation y' = fy has a solution
 and that there
exists an integer
and that there
exists an integer  such that gN is an analytic
element defined upon D. Then f is of the form :
such that gN is an analytic
element defined upon D. Then f is of the form :
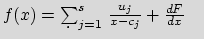 with :
with :
- i)
-
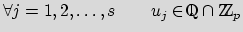 and
and
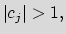
- ii)
-
 and
and