 Numeracie oft minderinghe.
Numeracie oft minderinghe.Onderwisinghe der bediedinghe der linien ende middel spacien
 Numeracie oft minderinghe.
Numeracie oft minderinghe. trect daer op na dien ghi veel hebt te reken
trect daer op na dien ghi veel hebt te reken 6 of 7
lini
6 of 7
lini eu
eu lanc
e
lanc
e eu
eu verre v
verre v malcanderen sta
malcanderen sta de
/ e
de
/ e laet van bou
laet van bou ne
ne ga
ga sommige lini
sommige lini midden doer
e
midden doer
e de
eerste linie cruyswijs te mak
de
eerste linie cruyswijs te mak ende ghelijc verre van malcander
ende ghelijc verre van malcander als vander
tweetster totter derder / e
als vander
tweetster totter derder / e van
van derder totter vier
derder totter vier &
&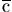 . e
. e sulcke
lini
sulcke
lini werden ghetrock
werden ghetrock om menigerley nutte e
om menigerley nutte e ghewichte wil,
&
ghewichte wil,
&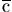 , daer
na begint van
, daer
na begint van eerster lini
[fo.11-verso]
en die lancx doer loopt e
eerster lini
[fo.11-verso]
en die lancx doer loopt e climt opwaert totter vierder linien e
climt opwaert totter vierder linien e op dat punct
daer de lini
op dat punct
daer de lini bouen afscheyd
bouen afscheyd di maect een cruys / e
di maect een cruys / e van die
lini
van die
lini gaet
weder op totter vierder e
gaet
weder op totter vierder e daer set we
daer set we een cruys /
e
een cruys /
e also
voort aen so daer meer linien sijn tot op die vierde als dan claerlijck wort
ghesien de bediedinge der lini
also
voort aen so daer meer linien sijn tot op die vierde als dan claerlijck wort
ghesien de bediedinge der lini als bou
als bou in figur
in figur oft cifer
oft cifer gheseyt is als een rekenp
gheseyt is als een rekenp ninc op die
eerste linie bringet 1 op die an
ninc op die
eerste linie bringet 1 op die an linie 10 op die derde 100 e
linie 10 op die derde 100 e op die vierde
1000 &
op die vierde
1000 &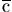 .
ghelijc dat bider opperste figueren ghesie is ooc ghelt een
yegelike spacie der opperster naester lini
.
ghelijc dat bider opperste figueren ghesie is ooc ghelt een
yegelike spacie der opperster naester lini bediedinge
dat half deel e
bediedinge
dat half deel e haer
naeste linie onder 5 mael tot lichter
haer
naeste linie onder 5 mael tot lichter 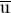 stadenisse
geeft a sijn natuerlike bediedinge / b 5 / c 10 / d 50 / e 100 / f 500 / g 1000 / h
5000 / i 10000 / k 50000 / l 100000 / m 500000 / n 1000000
stadenisse
geeft a sijn natuerlike bediedinge / b 5 / c 10 / d 50 / e 100 / f 500 / g 1000 / h
5000 / i 10000 / k 50000 / l 100000 / m 500000 / n 1000000

 Addicie oft sommeringhe.
Addicie oft sommeringhe.
 te samen bringen wanneer v voer gheleyt wert te sommeren
alderley of veel
te samen bringen wanneer v voer gheleyt wert te sommeren
alderley of veel ley
munte ghewichte mate oft an
ley
munte ghewichte mate oft an saken so
neemt die bouen gheseyde linie distingueert oft teyk
saken so
neemt die bouen gheseyde linie distingueert oft teyk et die
veld
et die
veld met sulcker waer noeminghe ghelijck oft ghi wilt adder
met sulcker waer noeminghe ghelijck oft ghi wilt adder menigherley
munte so set in dat eerste velt bou
menigherley
munte so set in dat eerste velt bou fl oft eenen gouden guld
fl oft eenen gouden guld daer voer: in
dat an
daer voer: in
dat an k.
maer tot Norenbosch lb. in dat derde
k.
maer tot Norenbosch lb. in dat derde  . in dat vierde
heller / dier ghelijc doet met een
. in dat vierde
heller / dier ghelijc doet met een ander munte / maer yst ghewichte so scriuet
bou
ander munte / maer yst ghewichte so scriuet
bou dat
eerste velt c / ouer dat an
dat
eerste velt c / ouer dat an lb. ouer dat derde loot ouer dat vierde quint / ouer
dat vijfste een penninck ghewichte e
lb. ouer dat derde loot ouer dat vierde quint / ouer
dat vijfste een penninck ghewichte e also yst ooc te
doen metter maten / daer na siet op alsulck
also yst ooc te
doen metter maten / daer na siet op alsulck seker getal
e
seker getal
e legget
een yegelic ghetal op sijn linie e
legget
een yegelic ghetal op sijn linie e spacie sijn
spacie sijn bediedinge ooc
in dat velt sijnde waer ghelijc als ic wil leggen 9824fl so set eenen reke
bediedinge ooc
in dat velt sijnde waer ghelijc als ic wil leggen 9824fl so set eenen reke penninc op der
linie spacie welc bediet 5000 e
penninc op der
linie spacie welc bediet 5000 e daer na 4 rekenp
daer na 4 rekenp ningen op die
linie welcke dusent bringet voorder sal liggen / acht hon
ningen op die
linie welcke dusent bringet voorder sal liggen / acht hon t also trect
eenen penninc in de spacie v
t also trect
eenen penninc in de spacie v vijf hondert / e
vijf hondert / e gheuet drye
rekenpenningen v
gheuet drye
rekenpenningen v hondert voor 24 legt 2 rekenp
hondert voor 24 legt 2 rekenp ningen op die
linie daer on
ningen op die
linie daer on e
e vier rekenp
vier rekenp ningen
op die on
ningen
op die on ste / daer na
legt in sulcker vormen die ghetalen die ghi ter tijt gheset adder
ste / daer na
legt in sulcker vormen die ghetalen die ghi ter tijt gheset adder wilt.
wilt. Een reghel.
Een reghel.
 5 rekenpenningen op een
5 rekenpenningen op een linien alsoe legt
een daer voren en in de spatie e
linien alsoe legt
een daer voren en in de spatie e alle tijt voor twee rekenpenninghen inde spatie legget
een inde linie daer naest bouen. Ghelijck ik wil adderen
alle tijt voor twee rekenpenninghen inde spatie legget
een inde linie daer naest bouen. Ghelijck ik wil adderen
| 28 | |
| 76 | |
| coemt | 104 |

 Die proeue
gaet wt die substractie welcke dan wert naerder multiplicacie ghewijst.
Die proeue
gaet wt die substractie welcke dan wert naerder multiplicacie ghewijst. Multiplicatie oft
meerderinghe.
Multiplicatie oft
meerderinghe.
 te vermeer
te vermeer in welcke ghi
moet hebb
in welcke ghi
moet hebb twee ghetal
twee ghetal dat eerste twelck wert ghemultipliceert. dat
an
dat eerste twelck wert ghemultipliceert. dat
an doer
welcmen multipliceert. Maer eerm
doer
welcmen multipliceert. Maer eerm begint te multiplicer
begint te multiplicer yst noot te
wet
yst noot te
wet de
applicaci
de
applicaci des vingers aen die slincker hant / twelc dan ooc dient der
diuisien. Daer
des vingers aen die slincker hant / twelc dan ooc dient der
diuisien. Daer 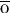 also dicwils als ghi sedt den selu
also dicwils als ghi sedt den selu vinger die
d
vinger die
d wiser
geno
wiser
geno t
wort op een linie so bediet sulcke linie ghelijc so veel als de eerste on
t
wort op een linie so bediet sulcke linie ghelijc so veel als de eerste on aen te
beghinn
aen te
beghinn / daer na gheeft die ander linie 10 / ende die derde 100 .&c.
/ daer na gheeft die ander linie 10 / ende die derde 100 .&c. vingher op de linie welcke hon
vingher op de linie welcke hon heet / so wert
duysent thiene / thien duysent hon
heet / so wert
duysent thiene / thien duysent hon honderdt duysent duysent .&c. [fo.13 recto]
honderdt duysent duysent .&c. [fo.13 recto] so legt altijts on
so legt altijts on de twee
ghetalen die grpptste op die linie e
de twee
ghetalen die grpptste op die linie e die an
die an nehout inden sin oft scrijftse op die tafele.
nehout inden sin oft scrijftse op die tafele. Die eerste Reghel.
Die eerste Reghel.
 hebt die
an
hebt die
an inden
sin / soe neemt of die opperste linie daer io rekenpenninghen liggen so hebben
die an
inden
sin / soe neemt of die opperste linie daer io rekenpenninghen liggen so hebben
die an linien daer na opwaert de bediedinghe ghelijc nv hier bouen gheseyt is inde
applicacien der figueren e
linien daer na opwaert de bediedinghe ghelijc nv hier bouen gheseyt is inde
applicacien der figueren e heft eenen rekenp
heft eenen rekenp ninc op
e
ninc op
e voer
den seluen legt dat ander ghetal dwelc v d
voer
den seluen legt dat ander ghetal dwelc v d inden sin is
e
inden sin is
e doet
also dicwils als daer een
doet
also dicwils als daer een penninck is / daer na climt ne
penninck is / daer na climt ne op die ander
linie e
op die ander
linie e doet ghelijc te vor
doet ghelijc te vor / e
/ e so tot op de al
so tot op de al leste p
leste p ningen
dat daer met en blijft.
ningen
dat daer met en blijft. Die ander reghel.
Die ander reghel.
 legt dat
behoud
legt dat
behoud ghetal dat ghi inden sin hebt e
ghetal dat ghi inden sin hebt e daer neuen merct altijts in die multiplicacie ghelijc
inder addicie gheseyt is wanneer comen 5 rekenp
daer neuen merct altijts in die multiplicacie ghelijc
inder addicie gheseyt is wanneer comen 5 rekenp ningen oft
meer op een linie oft 2 in een spacie hoe dat dan te doene is. Exempel. Ic wil
multipliceren 66 door 96 set also
ningen oft
meer op een linie oft 2 in een spacie hoe dat dan te doene is. Exempel. Ic wil
multipliceren 66 door 96 set also Maect ghelijck hier naer.
Maect ghelijck hier naer.
 Die proeve heeft haren oorspronc
wt der diuisi
Die proeve heeft haren oorspronc
wt der diuisi als oock hier na wert gheleert.
als oock hier na wert gheleert. Substractie oft aftreckinghe.
Substractie oft aftreckinghe.
 in welcke is
noot te weten die resolucien.
in welcke is
noot te weten die resolucien. Resolueren.
Resolueren.
 legt daer voren
een in dat spaci
legt daer voren
een in dat spaci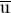 onder e
onder e rek
rek penningen
op de linie naest der spaci
penningen
op de linie naest der spaci of neemt een
rek
of neemt een
rek p
p ninc
in die spacie e
ninc
in die spacie e legt 5 rekenpenninghen op die naeste linie daer onder
ghelijck yst te resolueren 1000 e
legt 5 rekenpenninghen op die naeste linie daer onder
ghelijck yst te resolueren 1000 e 500 staet also dat ghi siet.
500 staet also dat ghi siet.
 welck
welck m
m wil treck
wil treck so siet
neerstelic dat daer wert ghetoghen e
so siet
neerstelic dat daer wert ghetoghen e een yegelick
ghetal van
een yegelick
ghetal van linien oft spacie sijnder bediedingen ghelijc als ic wil aftrecken
7999 van 21345 so merct op die vierde lini met dier spacie daer af ghi moecht
hebben 7000 e
linien oft spacie sijnder bediedingen ghelijc als ic wil aftrecken
7999 van 21345 so merct op die vierde lini met dier spacie daer af ghi moecht
hebben 7000 e e
e mach sulck ghetal nyet vond
mach sulck ghetal nyet vond worden so
gaet opwaert e
worden so
gaet opwaert e resolueert eenen rekenpenninc ghelijc gheleert is / so doet ooc
met 900 op die derde linie metter spacie e
resolueert eenen rekenpenninc ghelijc gheleert is / so doet ooc
met 900 op die derde linie metter spacie e also met 90
e
also met 90
e 9 op
de on
9 op
de on ste
tweetste linie e
ste
tweetste linie e den spaci
den spaci ghelijc ghi hier siet.
ghelijc ghi hier siet.
 Proeue der addicien.
Proeue der addicien.
 trect daer af dat getal diemen heeft gheaddeert so
dan die rekenp
trect daer af dat getal diemen heeft gheaddeert so
dan die rekenp ningen
alle opstaen so is sulcke addicie oprecht.
ningen
alle opstaen so is sulcke addicie oprecht. Proeue der substractien.
Proeue der substractien.
 die ghetal
die ghetal welcke ghi ghesubstraheert hebt tott
welcke ghi ghesubstraheert hebt tott ouer
ghebleuen oft residuo e
ouer
ghebleuen oft residuo e so dan we
so dan we commet dat ghetal v
commet dat ghetal v welcken ghi hebt ghesubstraheert so is sulcke
subsctractie recht.
welcken ghi hebt ghesubstraheert so is sulcke
subsctractie recht. Diuisio odt deylinghe: Deylt deen
ghetal doer dander.
Diuisio odt deylinghe: Deylt deen
ghetal doer dander. Die eerste reghel.
Die eerste reghel.
 welcke te deylen is op de linie tegen die rechte hant e
welcke te deylen is op de linie tegen die rechte hant e hout den
deylder inden sin / daer na grijpt mett
hout den
deylder inden sin / daer na grijpt mett vingher op de
slincker side op die ouerste linie der rekenp
vingher op de
slincker side op die ouerste linie der rekenp ningen met
ningen met
 anderinge
der bediedenisse [fo.15. recto] der lini
anderinge
der bediedenisse [fo.15. recto] der lini e
e siet oft merct
oft ghi den deelder hebb
siet oft merct
oft ghi den deelder hebb moecht so dat niet en can ghesijn so grijpt ooc de
naeste linie ne
moecht so dat niet en can ghesijn so grijpt ooc de
naeste linie ne waerts
e
waerts
e het daer op so lange tot dat ghi den deylaer hebb
het daer op so lange tot dat ghi den deylaer hebb moecht
e
moecht
e so
dicwils als ghi d
so
dicwils als ghi d deylder neemt so dicwils legget eenen rekenp
deylder neemt so dicwils legget eenen rekenp ninc op die
linie daer op die vingher is.
ninc op die
linie daer op die vingher is.  Die
ander reghel. Vvaneer ghi den deylder niet en moecht hebben so neemten half
so ghi cont / e
Die
ander reghel. Vvaneer ghi den deylder niet en moecht hebben so neemten half
so ghi cont / e legget eenen rekenpenninc in die spaci
legget eenen rekenpenninc in die spaci onder de
linien daer op d
onder de
linien daer op d vingher is ende resolueret soot noot is.
vingher is ende resolueret soot noot is.
 Proeue der multiplicatien.
Proeue der multiplicatien.
 Deylt dat ghetal dwelc
gecom
Deylt dat ghetal dwelc
gecom is doer dat een ghetal der tween welc ghi te sam
is doer dat een ghetal der tween welc ghi te sam hebt
ghemultipliceert so coemt die ander.
hebt
ghemultipliceert so coemt die ander.  Proeue der diuisien.
[fo.15. verso]
Proeue der diuisien.
[fo.15. verso] ghedeylt heeft
/ maer so wat is ouerbleuen dat doet daer toe &c.
ghedeylt heeft
/ maer so wat is ouerbleuen dat doet daer toe &c. Hier is te wet
Hier is te wet dat die
duplicacie e
dat die
duplicacie e mediacie op dat cifer e
mediacie op dat cifer e linien niet
an
linien niet
an s en is
dan multiplicacie e
s en is
dan multiplicacie e diuisie als dupler
diuisie als dupler is doer 2 multipliceren / e
is doer 2 multipliceren / e medieren is
doer 2 diuideren.
medieren is
doer 2 diuideren. Hier na
volget ghewichte munte ende mate van veel diuersche plaetsen ende steden.
Hier na
volget ghewichte munte ende mate van veel diuersche plaetsen ende steden.