Titelblad


Aanvullende gegevens:
J. Napier, A description of the admirable table of logarithms, London: Nicholas Okes (1616). Editie vertaald uit het Latijn door Edward Wright.
Opgenomen is het eerste boek, en in plaatvorm een fragment uit de bijbehorende tabellen (groot jpg-bestand).
De grote sierletters aan het begin van elk hoofdstuk zijn weggelaten. De opmaak is verder zo veel mogelijk behouden.

[pag. 1]

Bladversiering

A DESCRIPTI-
 ON OF THE ADMIRABLE
TABLE OF LOGARIHMES,
WITH THE MOST PLEN-
 TIFVL, EASIE, AND READY
Vse thereof in both kindes of
 Trigonometrie, as also in all Ma-
thematicall Account.

THE FIRST BOOKE.

CHAP. I.
Of the Definitions.

A line is said to increase equally, when the poynt describing the same, goeth forward equall spaces, in equall times, or moments.
 		I. Definition.
lijn
Let A be a poynt, from which a line is to be drawne by the motion of another poynt, which let be B.
Now in the first moment, let B moue from
[pag. 2]

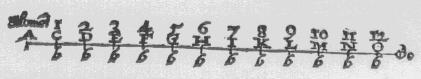
A to C. In the second mement form C to D. In the third moment from D to E, & so forth infinitely, describing the line ACDEF, &c. The spaces AC, CD, DE, EF, &c. And all the rest being equall, and described in equall moments (or times.) This line by the former definition shall be said to increase equally.
A Corollary or consequent. Therefore by this increasing, quantities equally differing, must needes be produced, in times equally differing.
As in the Figure before, B went forward from A to C in one moment, and from A to E in three moments. So in sixe moments from A to H: and in 8 moments from A to K. And the differences of those moments, one and three, and of these 6 and 8 are equall, that is to say two.
So also of those quantities AC, and AE, and of these, AH, and AK, the differences CE, and HK are equall, and therefore differing equally, as before.
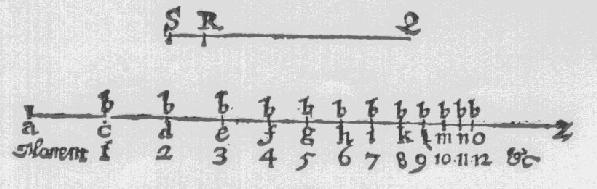
2. Definition. A line is said to decrease proportionally into a shorter, when the poynt describing the same in æquall times, cutteth off parts continually of the same proportion to the lines from which they are cut off.
lijn
For examples sake. Let the line of the whole sine aZ be to bee diminished proportionally: let the poynt diminishing the same by his
[pag. 3]

motion be b: and let the proportion of each part to the line from wch it is cut off, be as QR to QS. Therefore in what proportion QS is cut in R, in the same proportion (by the 10 of the 6 of Euclide) Let aZ be cut in c. and so let b running from a to c in the first moment, cut off ac from aZ, the line or sine cZ remaining.
And from this cZ let b proceeding in the second moment, cut off the like segment, or part, as QR to QS: and let that bee cd, leauing the sine. dZ. From which therefore in the third moment, let b in like manner, cut off the segment de, the sine eZ being left behinde. From which likewise in the fourth moment, by the motion of b, let the segment cf be cut off, leauing the sine fZ. From this fZ in the fifth moment, let b in the same proportion cut off the segment fg, leauing the sine gZ, and so forth infinitly. I say therfore out of the former definition, that here the line of the whole sine aZ, doth proportially decrease into the signe gZ, or into any other last sine, in which b stayeth, and so in others.
Hence it followeth that by this decrease in equall moments (or times) there must needes also bee left proportionall lines of the same proportion.
For what continuall proportion there is before of the sines to be diminished, aZ, cZ, dZ, eZ, fZ, gZ, hZ, iZ, and kZ, &c. and of the segments cut off from them ac, cd, de, ef, fg, gh, hi, and ik, there must needes be also the same proportion of the sines remaining, that is, cz, dz, ez, fz, gz, hz, iz, and kz, as may manifestly appeare 		A Corolary.
[pag. 4]

by the 19 Prop. 5 and 11. Prop. 7, Euclid.
3. Def. Surd quantities, or vnexplicable by number, are said to be defined, or expressed by numbers very neere, when they are defined or expressed by great numbers which differ not so much as one vnite from the true value of the Surd quantities.
As for example. Let the semidiameter, or whole sine be the rational number 10000000 the sine of 45 degrees shall be the square root of 50,000,000,000,000, which is surd, or irrationall and inexplicable by any number, & is included between the limits of 7071067 the lesse, and 7071068 the greater: therfore, it differeth not an vnite from either of these. Therefore that surd sine of 45 degrees, is said to be defined and expressed very neere, when it is expressed by the whole numbers, 7071067, or 7071068, not regarding the fractions. For in great numbers there ariseth no sensible error, by neglecting the fragments, or parts of an vnite.
4. Def. Equall-timed motions are those which are made together, and in the same time.
As in the figures following, admit that B be moued from A to C, in the same time, wherin b is moued from a to c the right lines AC & ac, shall be sayd to be described with an equall-timed motion.
5. Def. Seeing that there may bee a slower and a swifter motion giuen then any motion, it shall necessarily follow, that there may be a motion giuen of equall swiftnesse to any motion (which wee define to be neither swifter nor slower.)
6. Def. The Logarithme therfore of any sine is a number very neerely expressing the line, which increased
[pag. 5]

equally in the meane time, whiles the line of the whole sine decreased proportionally into that sine, both motions being equal-timed, and the beginning equally swift.


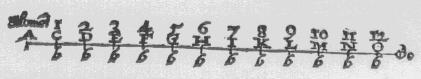
As for example. Let the 2 figures going afore bee here repeated, and let B bee moued alwayes, and euery where with equall, or the same swiftnesse wherewith b beganne to bee moued in the beginning, when it was in a. Then in the first moment let B proceed from A to C, and in the same time let b moue proportionally from a to c, the number defining or expressing AC shal be the Logarithme of the line, or sine cZ. Then in the second moment let B bee moued forward from C to D. And in the same moment or time let b be moued proportionally from c to d, the number defining AD, shall be the Logarithme of the sine dZ. So in the third moment let B go forward equally from D to E, and in the same moment let b be moued forward proportionally from d to e, the number expressing AE the Logarithme of the sine eZ. Also in the fourth moment, let B proceed
[pag. 6]

to F, and b to f, the number AF shall be the Logarithme of the sine fz. And keeping the same order continually (according to the former definition) the number of AG shall be the Logarithme of the sine gz. AH the Logarithme of the sine hz. AI the Logarithme of the sine iz. AK the Logarithme of the sine kz, and so forth infinitely,
A cosequet. Therefore the Logarithme of the whole sine 1000000 is nothing, or 0; and consequently the Logarithms of numbers greater then the whole sine, ar lesse then nothing.
For seeing it is manifest by the definition, that the sines decreasing from the whole sine, the Logarithmes increase from nothing: therfore contrariwise the numbers which yet we call Sines, increasing vnto the whole sine, that is to 10000000, the Logarithmes must needs decrease to 0 or nothing: and by consequent the Logarithmes of numbers increasing aboue the whole sine 10000000, which we call Secants, or Tangents, and no more sines, shall be lesse then nothing.
Therefore we call the Logarithmes of the sines Abounding, because they are always greater then nothing, and set this marke + before them, or else none. But the Logarithmes which are lesse then nothing, we cal Defectiue, or wanting, setting this marke - before them.
It was indeed left at libertie in the beginning, to attribute nothing, or 0. to any sine or quantitie for his Logarithme: but it was best to fit it to the whole sine, that the Addition or Substraction of that Logarithme which is most frequent in all Calculations, might neuer after be any troubel to vs.
[pag. 7]

CHAP. II.
Of the Propositions of Logarithmes.

The Logarithmes of Proportionall numbers and quantities are equally differing. Propos. I.
As for example. The Logarithmes of the proportionall sines, namely cz which is to ez, as hz is to kz, are respectiuely the numbers defining AC, AE, AH, AK, (as is manifest by the 6 Definition.) Now AC, and AE differ by the difference CE, and AH and AK by the difference HK. But by the first definition and his Corolarie CE and HK, are equall: therefore the Logarithmes of the foresaid proportional sines are equally differing. And so in all proportionals.
For what affections and symtomes the Logarithmes haue gotten in their first beginning and generation, the same must they needes retaine and keepe afterwards.
But in their beginning and generation, they are indued with this affection, and this law is prescribed vnto them, that they bee equally differing, when their sines or quantities are proportionall (as it appeareth by the definition of a Logarithme, and of both motions, and shall hereafter more fully appeare in the making of the Logarithmes.) Therefore the Logarithmes of proportional quantities are equally differing.
Of the Logarithmes of three proportionals, the double of the second or meane, made lesse by the first, is equall to the third. Propos. 2.
[pag. 8]

Seeing that by the first propos. the difference of the Logarithmes of the first and second, is equall to the difference of the Logarithmes of the second and the third, that is, the second made lesse by the first, is equall to the third, lesse by the second: therefore the second being added to both sides of the equation twice, the second, or the double of the second made lesse by the first, shall come forth equall to the third, which was to bee proued.
Propos 3. Of the Logarithmes of three proportionals, the double of the second, or middle one, is equall to the summe of the extremes.
By the second Proposition next going before, the double of the second, made lesse by the first, is equall to the third. To both the equall sides adde the first, and there shall arise the double of the second equall to the first and the third, that is, the summe of the extremes, which was to bee demonstrated.
Propos. 4. Of the Logarithmes of foure proportionals, the summe of the second and third, made lesse by the first, is equall to the fourth.
Seeing by the first Proposition of the Logarithmes of 4 proportionals, the second made lesse by the first, is equall to the fourth lesse by the third: adde the third to both sides of the equality, and the second and third made lesse by the first, shall bee made equall to the fourth, which was propounded.
Propos. 5. Of the Logarithmes of foure proportionals, the summe of the middle ones, that is, of the second and third, is equall to the Logarithme of the extreames, that is to say, the first and fourth.
By the 4 proposition going afore the 2 &
[pag. 9]

third made lesse by the first, were equall to the fourth: to both sides of the equality adde the first, and the second more by the third shall bee made equall to the fourth, more by the first, which was to be demonstrated.
Of the Logarithmes of foure continually proportionals, te triple of either of the middle ones, is equall to the summe of the further extraame, and the double of the neerer.
By the second proposition, the double of the second made lesse by the first, is equall to the third; and by the third proposition the double of this, that is, the fourefold of the second made lesse by the double of the first, shall be equall to the summe of his extreames, that is, the fourth more by the second. Now, if from both sides of the equality you substract the second, the triple of the second made lesse by the double of the first, shall be made equall to the fourth. Againe, to the sides of this equality adde the double of the first, and there shall arise the triple of the second, equall to the fourth, more by the double of the first, which wee vndertooke to proue.

 		Propos. 6.
An Admonition.
Hitherto we haue shewed the making and symptomes of Logarithmes; Now by what kinde of account or method of calculating they may be had, it should here bee shewed. But because we do here set down the whole Tables, and all his Logarithmes with their Sines to euery minute of the quadrant: therfore passinf ouer the doctrine of making Logarithmes, til a fitter time, we make haste to the vse of them: that the vse and profit of the
[pag. 10]

thing being first conceiued, the rest may please the more, being set forth hereafter, or else displease the lesse, being buried in silence. For I expect the iudgement and censure of learned men hereupon, before the rest rashly published, be exposed to the detraction of the enuious.


CHAP. III.
Containing the description of the Table of
Logarithmes, and of the seuen
colums thereof.

1 Section. The first Columne is expresly of the Arches increaing from 0 to 45 degrees, and is also vnderstood to bee of their remainders to a semicircle.
2 Section. The seuenth columne is of arches decreasing from a quadrant to 45 degrees, and is also vnderstood to bee of their remainders to a semicicle.
3 Section. So the Arches of the one columne are the complements of the Arches of the other answering ouer-against them.
4 And in the first is expressed the lesse sharpe angle of any right-lined right-angled triangle.
5 But in the seuenth ouer against it, is placed the greater sharpe angle of the same right-angled triangle.
6 In the second column are the sines of the arches of the first columne.
7 And these are the lesse legges subtending the lesse angle of a right angled triangle, whose Base, or Hypothenuse is the whole sine.
8 In the sicth columne are the sines of the arches of the seuenth columne.
[pag. 11]

And these are the greater legges subtending the greater sharpe angle of the same right-angled triangle, whose hypothenuse is the whole sine. 9
Hence it followeth, that of the whole sine, and the sine of the second columne, and the sine of the sixthe columne answering ouer-against the same, there is made a triangle that is equiangled, and like to any right-angled right-lined triangle.
 		10
The third columne containeth the Logarithmes of the arches and sines towards the left hand.
 		11
Which are the Logarithmes of the proportion of the lesse legge of a right-angled triangle, to the Hypothenuse of the same.
 		12
And they are also the Logarithmes of the complements of the arches and sines towards the right hand, which we call Antilogarithmes.
 		13
The fifth columne containeth the Logarithmes of the arches and sines towards the right hand, or the Logarithmes of the complements.
 		14
Which are the Logarithmes of the proportion of the greater legge of a right-angled triangle, to the Hypothenuse of the same.
 		15
They are also the Antilogarithmes of the arches and sines towards the left hand, or the Logarithmes of the complements.
 		16
Lastly, the fourth or middle columne containeth the differences betweene the Logarithmes of the third and fifth columnes. And so this columne is two-fold, Abounding and Defectiue.
 		17
Those differences are Abounding, which arise out of the substraction of the Logarithmes of the fifth columne from the Logarithmes of the third columne.
 		18
But the differences arising by substraction of the Logarithmes of the third columne out of the Logarithmes of the fifth columne, are Defectiue, which therefore are lesse then nothing.
 		19
The Abounding differences are called the differentiall
 		20
[pag. 12]

numbers of the arches towards the left hand.
21 And are the Logarithmes of the proportion of the lesse legge of a right-angled triangle, to the greater legge of the same.
22 And are also the Logarithmes of the Tangents of the left hand arches.
23 But the defectiue Differences, are called the differential numbers of the right hand arches.
24 And are the Logarithmes of the proportion of the greater legge of a right-angled triangle, to the lesse legge of the same.
25 And are also the Logarithmes of the Tangents of the right-hand arches.
26 Also euery left hand arch, and the remainder thereof to a semicircle, is called the arch of the complement of the arches, sines, & right hand Logarithmes, and of the Defectiue differentials.
27 And contrariwise euery right hand arch, and the remainder thereof to a semicircle, is called the arch of the complement of the arches, sines and left hnd Logarithmes, and of the Abounding differentials.
Admonitions.
28 Here it is to be noted, that if you make the Logarithmes of the third columne Defectiue, setting before them this marke, - they shall bee made the Logarithmes of the Hypothenuses or Secants of the right hand arches of the seuenth columne.
29 And these also shall bee made the Logarithmes of the proportion of the Hypothenuse of a right angled triangle to the lesse legge of the same.
30 And if you make the Logarithmes of the fifth columne Defectiue, they shall bee the Logarithmes of the Hypothenuses, or of the Secants of the left
[pag. 13]

hand arches of the first columne.
The same shall also be the Logarithmes of the proportion of the Hypothenuse of a right-angles triangle to the greater legge of the same. But because the sines onely, and their arches, and the Logarithmes with their Differentials, are sufficient for attaining the knowledge of right-lined triangles, and for the knowledge of sphæricall triangles, the arches onely with their Logarithmes and Differentials are sufficient without regard of the sines. Therefore we haue excluded the Tangents, and the Hypothenuses, or Secants, out of the Table: and in sphærical triangles we will haue the sines also not regarded; yet we will shew you by the way, that you may, if you list, vse them all readily enough in right-lined triangles, but not in sphæricall.
 		31


CHAP. IV.
On the vse of the Table, and of the numbers
thereof.

The Sines, Tangents and Secants being precisely found in their Tables, to finde their Logarithmes as precisely.
By the 11 anf 14 Section of the third chapter, the Sine giuen being found in the second, or sixth columne of our Table, the Logarithme thereof shall bee found in the third or fifth columne of the same line.
So therefore, the Logarithmes of the Sines that are in the table are exactly had. And the numbers of the Tangents and Secants being found in their owne Tables, you haue their arches. 		Sect. 1.
[pag. 14]

And the arches being knowne, out Table giueth you the Logarithmes of the Tangents, ot the differentials with their signs or marks in the middle columne, by the 22 and 25 Sect. And the Logarithmes of the Secats reciprocally in the third & fifth columnes; yet setting before them this sign --- by the 28 and 30 Sect. Therefore the Logarithmes of the Sines, Tangents and Secants that are in the Tables, are thus had.

Examples of Sines.
I seeke the Logarithme of the sine 694658. I finde that sine precisely in the second columne, answering to the arch 44 degrees, o min. & in the same line of the third columne, there standeth ouer-against it, the Logarithme 364335 which I sought. Also let the Logarithme of the sine 721357 bee sought. This sine shall bee found answering to the arch 46 degr. 10 min. and neere adioyning thereto 326620. the Logarithme thereof that was sought.

Examples of Tangents.
Let the Logarithme of the Tangent 218645 bee sought. To this Tangent there answereth in this Table the arch of 12 degr. 20 min. and to this arch in the middle columne of our Table, answereth the Logarithme, or differentiall abounding 1520306 which was sought. Also if you shall seeke the Logarithme of the Tangent 4573629 you shall finde in the Table of Tangents his arch 77 degr. 40 min. and the same differentials of this arch in our Table, but yet defectiue, that is, ---1520306.
[pag. 15]

Examples of Secants.
To the Secant 1811801 there answereth in the Table of Secants, the arch 56 degr. Œ30 min. and to this arch in our Table agree-eth reciprocally ---594321 the defectiue Logarithme of the Secant 1811801, aboue written. So you shall find ---271425, the Logarithme of the Secant 1311834 & of the secant 1396059 you shall find the Logarithme ---333653.
To æstimate the Logarithme of the numbers giuen, and not found in the Tables of the Sines, Tangents, and Secants.
Seeke the number that is most like the number giuen in the second or fixt columne of our Table, whether it be ten fold, an hundred fold, a thousand fold, 10000 fold, 100000 fold, 1000000 fold: or is you will in the Tables of Tangents and Secants: and note the arche hereof. For the Logarithme thereof taken out of our Table, is that you seek for: yet keeping in minde, or for memory sake, setting downe in cyphers, the number of the places or figures of the multiplicitie. As if the Logarithme of the number 137 bee sought, which is not found in the Tables, you shall finde among the Sines 1454, 13671 and 137156. And among the Tangents 1370505, but among the Secants, the number 1370305 which is likest of all to the number giuen, if the last foure figures toward the right hand be vnderstood to be blotted out. Therefore let the logarithme of this Secant 1370305 and of his arch 43 degr. 8 min. be sought out by the former Section, or by the 28 and 30 Sections of the third chapter, and it shall bee found ---315033, which is also taken for
[pag. 16]

the Logarithme of the number giuen 137 remembring, notwithstanding, that the 4 last figures are to be cut off, or for memory sake to be noted thus expresly ---315033 ---0000. Likewise if by the Tangents aboue expressed, 1370505 you shall seeke the Logarithme of the number 137 by the arch of that Tangent 53 degr. 53 min. shall be found by the 25 Section in the middle columne ---315179, the Logarithme of that Tangent 1370505 which because it exceedeth 137 the number giuen by foure places, or figures. Therefore Œ---315179 ---0000 shall be the Logarithme of the number giuen 137; yet this Logarithme is so much lesse exact by how much 1370505 is more vnlike to the number 1370000, or the 10000 fold of the number giuen. But this error exceedeth not 505/10000. Lastly, if you shall seeke the Logarithme of the number giuen 137 by the Sine aboue written 137156 that shall bee found to bee 1986633 ---000 by this & the 11 Section of the third chapter. In like manner you shall work by the sign + when the number of the figures of the quantitie giuen, exceedeth the number of the figures of the sine that is likest thereto, which seldome happeneth. As if the Logarithme of the number (or discreet quantitie) 232702 bee sought for, you shall finde in the Table, the sine 2327 most like thereto; but it wanteth two figurs. Therefore to the Logarithme hereof, found in the Table (by the 11 Sect. chap. 3) which is, 6063128 let be added two cyphers, the signe + being put betweene, and it shall be made 6063128 + 00 for the Logarithme of the number 232702 which was sought for.
[pag. 17]

But the best way of estimating Logarithmes, is that whereby they were first made, wherof we shall speak in another place.
Therfor as in the first Section going afore, simple and pure Logarithmes are giuen: so in this Section next going before by putting cyphers to them, they become impure.
To adde Logarithmes of like signes, is to giue the summe of them both, with their signe common to them both.
As by the Addition of ---56312 to ---73495 there shall come forth ---129807. Also 4216 being added to +5392, there comes forth 9608. So 3219 -00 added to 4360 -000 make 7579 -00000.
To adde the Logarithmes of vnlike signes, is to giue the difference of them with the signe of the greatest number.
As of the Addition of ---210 to 332 is produced +122.
Also of the addition of --210 to 192, comes Œforth ---18.
So --210 +000 added to 192 +00, are ---18 ---0.
Of two Logarithmes this is properly said to bee the Defectiue of that, and that the Abounding of this: when they haue both number and cyphers common, or the same, and all the signes + and --- altogether contrary.
As of the Abounding Logarithme 56312, the defectiue is ---56312. Also of the Abounding Logarithme 56312 ---00 the Defectiue is ---56312 +00. So of the Abounding Logarithme 56312 +00, the Defectiue is, ---56312 ---00.
[pag. 18]

To subtract an abounding Logarithme, is to adde his defectiue.
As to subtract the abounding Logarithme 56312 out of ---73495, is the same as to adde his defectiue which (by the sixth Section.) is ---56312 to the same ---73495, and they shall bee made (by the 4 going before) ---129807. So to subtract 56312 +00 out of ---73495 ---000 is the same as to adde ---56312 ---00 to 73495 ---000, and they are made (by the 4 and 5 Sect. going before) ---129807 ---00000.
To subtract a defectiue is to adde his aboundant.
As to subtract a defectiue ---4261 out of +5392, is the same that it is to adde 4216 to 5392, and (by the fourth Section) to bring forth 9608. So it is the same to subtract ---4216 +00 out of 5392 +0, that it is to adde 4216 ---00 to 5392 +0 and to bring forth 9608 ---0.
To increase or diminish a Logarithme in number, his former value remaining, is to adde to it, or subtract from it, any of the Logarithmes following, as 2302584 +0, or 4605168 +00, or 6907753 +000, or 9210337 +0000, or 11512921 +00000, sinifying nothing at all.
As let the Logarithme bee 3916 ---0 whereto if you adde any of them, as for example sake, 2302584 +0, there shall be made thereof 2306500 greater in number, but in value altogether the same that 3916 ---0 is: for the quantity or numerall value of this Logarithme 3916 ---0 (by the 12 and 13 Sections following of this Chapter) is 996092, from which take onely the
[pag. 19]

last figure, as ---0 signifieth, and it shall be made 99609. And the numeral value of that Logarithme 2306500 (by the 12 and 13 Sections following of this chapter) is also 99609 the same that was before.

An example of diminishing.
Let the Logarithme 2545177 bee to be diminished, from which if you subtract 2302584 +0, there is left 242593 ---0 of the same value that this former 2545177 was. For the value of the simple and pure Logarithme 242593 is ten fold the value of either of them. Their values therefore are equal each to other. For the addition of the Logarithme 2302384 +0, signifieth nothing else, but that the value of the number whereto it is added, is to be diuided into ten parts, and that one cypher is to bee added to this tenth parth: but the subtraction of the same signifieth that the value of the Logarithme from whence it is substracted, is made tenne fold more, and that one cypher is cast away from this ten fold. There remaineth therfore the same value in both of them.
So 46051684 +00 added, signifieth that two cyphers are added to the hundreth part of the value: and being subtracted, it signifieth that two cyphers are cast away from the hundreth fold, and so of the rest aboue expressed.

An Admonition.
Bvt because the addition and subtraction of these former numbers may seeme somewhat painfull, I intend (if it shall please God) in a second Edition, to set out such Logarithmes as shal make those numbers aboue written to fall upon
Ϊ[pag. 20]

decimal numbers, such as 100,000,000, 200,000,000, 300,000,000, &c, which are easie to bee added or abated to or from any other number.
If therefore you shall adde to a Logarithme that is diminished by some cyphers, or shall subtract from a Logarithme increased by cyphers, any of the Logarithmes aboue written that containe so many cyphers, there shall out of an impure Logarithme bee produced, a pure one of the same value.
As in the first example going before, let the impure Logarithme 3916 ---0 bee to bee purged from this cypher and signe ---, adde therefore thereto 2302584 +0 there shall thereof be made, as before, 2306500, the pure Logarithme of this former value. So from the impure Logarithme 6358447 +00 if you subtract 4605168 +00, (which containeth as many cyphers) there shall remaine the pure Logarithme 1753278, and of the same value, whereof that former impure Logarithme was.
If to a Logarithme that is Defectiue in number, you shall adde any of the foresaid Logarithmes of the ninth Section, that is greater in number, there shall come forth a Logarithme of the same value Abounding in number.
As to the Logarithme ---2859527 ---0000 adde any of the numbers of the ninth Section, that is greater in number. As for example, 4605168 +00, and there shall bee made thereof 1745641 ---00 of the same value, and abounding in number.
You may giue the Sines, Tangents, and Secants, or any numerall values whatsoeuer, of the Logarithmes that are found in our Table by the 11, 14, 22, 25, 28, 30 Section of the 3 Chapter,
[pag. 21]

whether they be pure or impure.
As to the Logarithme of 36 degrees, 40 minutes 515572, in the third columne, answereth this sine 597159 in the second columne, & to the Defectiue therof ---515572 there answereth in the Table of Secants, 1674597, the Secant of 53 degrees, 20 minutes.
Also to the Differentiall Logarithme 295079 in the fourth columne, answereth the Tangent 744472 in his Table, and to his Defectiue ---295079 answereth 1343233 the Tangent of 53 degrees and 20 minutes. So of the Logarithme 220493 in the fifth columne, the numerall value in the fixth columne is 802123, that is the Sine of 53 deg. and 20 min. and the numerall value of the Defectiue therof, that is ---220493 is the Secant 1246691, agreeing to 36 degrees and 40 minutes.

An example of impure Logarithmes
Let the value of the impure Logarithme 9780 ---0 bee to bee sought out; to this number, there answereth in our Table the Sine 990268, from which take the figure next the right hand (as ---0 doth shew) & they shall be made 99027, the value of the Logarithme 9780 ---0 which was sought. So the value of the Logarithme 2545177 +00 is 7845900, because that to the pure Logarithme 2545177 there answereth in our table the Sine 78459. Also of the Logarithme 34914 ---00 found in the fourth columne at 46 degrees, the value shall be 10355, because the Tangent of 46 degr. is 1035530. So of the Logarithme ---635030 ---0 found in the third columne at 32 degrees, the
[pag. 22]

value is 18871, because the Secant of the complement of 32 degrees, that is of 58 degrees, is 1887080, whose two last figures next the right hand 80, are to be blotted out for ---00 adicyned to the Logarithme.
To estimate the numerall values of the Logarithmes giuen, and not found in our Table.
For common measuring, it is sufficient for the most part, to take for the Logarithme giuen, the numeral value of the Logarithme in the Table, that comes neerest that, which is giuen. But if you desire to come neerer the marke, increase or diminish in number the Logarithme giuen, by the 9 Section of this Œchapter, his former value remaining vntill it be either found in the Table, or become like enough to some Logarithme in the Table, and the value of this Logarithme found by the former Section, is that which we seek for. As for example, let the value of this Logarithme 2314972 +0 bee sought, to which there is none found like or neere enough in the Table; but if you subtract from it 2302584 +0, there shal be left 12388 almost, to which vnder 81 degr. there shall be found one that is neere, and like enough to it, that is, 12388, the Sine whereof 987688 found by the former Section, is the value of the Logarithme proposed 2314972 +0 which was sought for.

An Admonition.
For this and the 2 Sect. of this chapter, we would haue you admonished, that the Logarithmes of the numbers giuen, & contrariwise the numerall values of the Logarithmes giuen, when they are not found in the Table, are most exactly giuen by the way, by
[pag. 23]

which the Logarithmes are made or resolued, which is that you descend from the sine giuen by meanes Geometrically proportionall, vntill you come to the next lesse sine in the Table. Likewise from the Logarithme heereof, in the Table, that you descend also by as many agreeable meanes Arithmeticall: and the last of these shall be the Logarithme of the first of them, and contrariwise by resolution that you descend from the Logarithme giuen by Arithmetical meanes to the next lesse Logarithme in the Table, and from the value of this in the Table likewise, that you descend, by as many meanes Geometricall and agreeable: and the last of these shall bee the numerall value of the first of those Logarithmes. But what Arithmeticall equalitie of difference agreeth and is fitting to euery continued Geometricall proportion, is a matter of no meane skil to finde out. Wherefore of these (if God will) we shall intreate Œhereafter more at large, when we shall handle the making of Logarithmes.
CHAP. V.
Of the most ample use of the Logarithmes,
and ready practise by them.

Of the Logarithmes of three proportionals, the middle Logarithme being giuen, and one extreame, to finde the other extreame, or his proprtionall, or arch by one doubling, or subtraction onely.
Seeing that by the second proposition, Chap.2. the double of the middle (Logarithme) made lesse by one of the extreames, is made equall to the other; Therefore from
[pag. 24]

the double of the middle Logarithme giuen, subtract the giuen Logarithme of the extreame, and there shall remaine the Logarithme of the extreame that was sought for: which being found in the third, fourth, or fifth columne of the Table, you haue the arch answering thereto in the first and seuenth columne, and the Sine in the second or fixth, and their Secants or Tangents in their Tables, by the third Chapter, Section 1, 2, 6, 8, 11, 14, 22, 25, 28, 30 for the extreame that was sought for.
Example.
Let the first proportionall giuen, bee 1000000, and the second 707107: let the third be sought for, which commonly is found by multiplying the middle number by it selfe, & diuiding this square by the first. But we find it easilier by doubling the Log: of the middle number 346573, and by subtracting from this double (wch is 693147) the Logarithme of the first, which is 0, & there remaineth 693147, the Logarithme sought for, whose arch you shall finde to be 30 degrees, and the Sine adioyning thereto 500000, which is the proportionall number sought for. Therefore 1000000, 707107, 500000, are three proportionall numbers, the last whereof wee found onely by doubling, and subtraction, which wee promised. Also let there bee two proportionall numbers giuen, the first 1056256, & 766045 the second, or at least their Logarithmes ---54730, and 266515. The third you shall thus finde: From the double of this last 533030 subtract ---54730, and by the 8 Section of the 4 chapter, there is brought forth 587760, the Logarithme of 33 degrees. 45 minutes, the
[pag. 25]

sine whereof 555570 is the third proportionall number that was sought for.
Out of the Logarithmes of three proportionals, the extreame Logarithmes being giuen, to finde the middle Logarithme and his proportionall and arch, by one addition onely, and diuision by two.
Seeing by the third proposition of the second chapter, the double of the middle Logarithme is equall to the summe of the extreames, therefore adde the Log. of the extreames, and diuide the product by 2, & there shall come forth the Logarithme of the middle proportionall number: and thereby the middle proportionall, and the arch thereof, is knowne in the columnes, and by the Sections, as before. As for Example.
Let the extremes 1000000 and 500000 bee giuen, and let the meane proportionall be sought: that commonly is found by multiplying the extreames giuen, one by another, and extracting the square root of the product. But we finde is easilier thus; We adde the Logarithmes of the extreames 0 and 693147, the summe whereof is 693147 which we divide by 2 & the quotient 346573 shall be the Logar. of the middle proportionall desired. By which the middle proportionall 707107, and his arch 45 degrees are found as before. Also let the extremes giuen bee 1056256 and 555570, their Logarithmes are ---54730 and 587760. The Œsumme of these put together, is 533030 by the 5 Sect. Chap. 4 which we diuide by two, and the quotient is 266515, the Logarithme and his arch 50 degr. and the sine or meane proportionall sought for is 766044 found by addition onely, and diuision by two.
[pag. 26]

Out of the Logarithmes of foure proportionals, three being giuen, or their arches, to find the fourth Logarithme with the sine and arch thereof, by one addition onely, and subtraction.
In this probleme wee alwayes make the thing demanded the fourth, so that as the first of the numbers giuen is to the second, so is the third to the number demanded. And seeking the summe of the Logarithmes of the second and third of the numbers so places, diminished by the Logarithmes of the first, is equall to the Logarithme of the fourth, by the 4. Prop. Chap. 2. Therefore adde the Logarithmes of the second and third, and from the summe of them take the Logarithme of the first, and there shall remaine the Logarithme of the fourth proportionall number demanded, and thence the fourth number it selfe, and the arch thereof.
For examples sake.
As 766044 is to 984808: so let 500000 be to the fourth proportionall which wee seeke for. This they commonly finde by multiplying the second and third, and diuiding the product by the first. But you may find it more easily thus: Adde the Logarithme of the second 15309, and of the third 693147, the summe whereof shall be 708456: out of which subtract the Logarithme of the first, which is, 266515, and there shall remaine 441941, the Logarithme of the fourth, whose sine 642788 is the fourth proportionall desired, and the arch thereof 40 degrees. The same would come forth if (the sines being neglected) their three arches onely were giuen 50 degrees, 80 degrees, and 30 degrees. For out of the logarithmes of the arches 80
Œ[pag. 27]

degrees, and 30 degrees, subtract the Logarithme of 50 degrees, there shall remaine the Logarithme of 40 degrees: and so the erch it selfe 40 degrees, shall be knowne without the sines, or their multiplication or diuision, according as we promised in the beginning.

Another Example.
As the Tangent of 43 degrees is to the Sine of 57 degrees, so let the Tangent of 35 degrees bee to a fourth Sine vnknowne, whose arch without regard either of Sines or Tangents, we shall thus finde: Wee adde the Differential Logarithme of 35 degrees, that is, 356378 found in the middle columne to the Logarithme of 57 degr. that is 175937 placed in the fifth columne from the product, that is, 532316, wee subtract the Differentiall of 43 degrees, which is 69870, and there remaineth 462446, the Logarithme of the fourth (Sine) which being found in the third columne, by the 11 Section of the third chapter, you shall finde close by it in the first columne 39 degrees 2 minutes almost, which is the arch of the fourth proportionall, or Sine neglected.
Thus the arches of proportionall numbers are found without their Sines, Tangents, Secants, or any proportionall numbers whatsoeuer.
Which so short a way of working, doth helpe very much for measuring the angles of plaine triangles, and for whole Trigonometrie of sphærical triangles, as in his proper place shall appeare.
Of foure numbers in continuall proportion, the extremes being giuen, or their arches, to finde any
[pag. 28]

of the middle numbers, or any of their arches, onely by diuiding by three, in stead of the troublesome extracting of the cubicke root.
Seeing that in the Logarithmes of these, the triple of any middle one, is equall to the summe of the extreme remoued, and the double Œof the next extreame, by the fixth proposition of the second chapter. Therefore adde the double of either extreame remaining, and diuide the product by three, and there shall come forth the Logarithme of the middle proportionall next the former extreame, and after the same manner, the other meane proportionall also.
As for examples sake.
Let the first extreame be 402925, and the lst, 1056256, the meane proportionals are sought for, which without extraction of the cubicke roote you shall thus finde. The Logarithme of the numbers giuen are 909005, and ---54730: to the double of that 1818010, adde this, and the summe shall bee 1763280, which diuided by three, bringeth forth 587760 the Logarithme, whose Sine 555570 is the first meane proportionall sought for. Also in the like manner to the double of this ---54730, which is ---109460, adde that 909005, and the product will bee 799545, which diuided by three, bringeth forth 266515 the Logarithme, whose Sine 766044 is the later meane which was sought for. These therefore are four continuall proportionalls 402925, 555570, 766044 and 1056256.
Another example.
Let the extreames given bee 1414213,
[pag. 29]

and 500000: the first of these being found in the Table of Secants, the Logarithme thereof in our Table is ---346573, and the Logarithme of 500000 is 693147 to the double whereof, 1386294 adde ---346573, the summe shall be 1039720, which diuided by 3, will be 346573 the Logarithme of the meane proportional next the lesse extreme, which is 707107. So to the double of ---346573, which is ---693147, add 693147, and there shall be made thereof nothing, which divided by 3, maketh also 0, Œthe sine anf the value whereof is 1000000 for the remaining and greater meane proportionall. These foure therefore are continually proportionall, 1414213, 1000000, 707107, 500000.

The Conclusion.
Now out of this that is already deliuered, let the learned iudge how great benefit the Logarithmes bring them; seeing that by the addition and substraction of them, and by diuiding by 2 and 3, and by other easie additions, or subtractions, multiplication, diuision: the extraction of the square and cubicke rootes, and all the great toyle of calculating is auoided, a generall taste where of we haue giuen in this Booke.
But in the booke following we shall treate of their proper and particular vse in that noble kinde of Geometrie which is called Trigonometrie.

The end of the first Booke.