Über die Hypothesen, welche der Geometrie
zugrunde liegen.
Aanvullende gegevens:
B. Riemann, Über die Hypothesen, welche der Geometrie zugrunde
liegen, Habilitationsrede van Riemann bij zij aanstelling aan de filosofische
faculteit van Göttingen, 10 juni 1854. Voor het eerst gepubliceerd in:
Abhandlungen der Gesellschaft der Wissenschaften zu
Göttingen XIII.
Über die Hypothesen, welche der Geometrie
zugrunde liegen.
Plan der Untersuchung.
Bekanntlich setzt die Geometrie sowohl den Begriff des
Raumes, als die ersten Grundbegriffe für Konstruktionen im Raume als
etwas Gegebenes voraus. Sie gibt von ihnen nur Nominaldefinitionen,
während die wesentlichen Bestimmungen in Form von Axiomen auftreten.
Das Verhältnis dieser Voraussetzungen bleibt dabei im Dunkeln; man sieht
weder ein, ob und inwieweit ihre Verbindung notwendig, noch a priori, ob sie
möglich ist.
Diese Dunkelheit wurde auch von Euklid bis auf
Legendre, um den berühmsteten neueren Bearbeiter der Geometrie zu
nennen, weder von den Mathematikern noch von den Philosophen, welche sich
damit beschäftigten, gehoben. Es hatte dies seinen Grund wohl darin,
daß der allgemeine Begriff mehrfach ausgedehnter Größen,
unter welchem die Raumgrößen enthalten sind, ganz unbearbeit
blieb. Ich habe mir daher zunächst die Aufgabe gestellt, den Begriff einer
mehrfach ausgedehnte Größe aus allgemeinen
Größenbegriffe zu konstruieren. Es wird daraus hervorgehen,
daß eine mehrfach ausgedehnte Größe verschiedener
Maßverhältnisse fähig ist und der Raum also nur einen
besonderen Fall einer dreifach ausgedehnten Größe bildet. Hiervon
aber ist eine notwendige Folge, daß die Sätze der Geometrie sich
nicht aus allgemeinen Größenbegriffen ableiten lassen, sondern
daß
[pag. 2]
diejenigen Eigenschaften, durch welche sich der Raum von anderen denkbaren
dreifach ausgedehnten Größen entnommen werden können.
Hieraus ensteht die Aufgabe, die einfachsten Tatsachen aufzusuchen, aus denen
sich die Maßverhältnisse des Raumes bestimmen lassen -- eine
Aufgabe, die der Natur der Sache nach nicht völlig bestimmt ist; denn es
lassen sich mehrere Systeme einfacher Tatsachen angeben, welche zur
Bestimmung der Maßverhaältnisse des Raumes hinreichen; am
wichtigsten ist für den gegenwärtigen Zweck das von Euklid
zugrunde gelegte. Diese Tatsachen sind wie alle Tatsachen nicht notwendig,
sondern nur von empirischer Gewißheit, sie sind Hyporthesen; man kann
also ihre Warscheinlichkeit, welche innerhalb der Grenzen der Beobachtung
allerdings sehr groß ist, untersuchen und hiernach über die
Zulässigkeit ihrer Ausdehnung jenseits der Grenzen der Beobachtung
sowohl nach der Seite des Unmeßbargroßen, als nach der Seite des
Unmeßbarkleinen urteilen.
I. Begriff einer n-fach ausgedehnten Größe.
Indem ich nun von diesen Aufgaben zunächst die
erste, die Entwicklung des Begriffs mehrfach ausgedehnter Größen,
zu lösen versuche, glaube ich um so mehr auf eine nachsichtige
Beurtheilung Anspruch machen zu dürfen, da ich in dergleichen Arbeiten
philosophischer Natur, wo die Schwierigkeiten mehr in den Begriffen, als in der
Konstruktion liegen, wenig geübt bin und ich außer einigen ganz
kurzen Andeutungen, die Herr Geheimer Hofrat Gauß in der zweiten
Abhandlung über die biquadratischen Reste, in den Göttingensche
gelehrten Anzeigen und in seiner Jubiläumsschrift darüber gegeben
hat, und einigen philosophischen Untersuchungen Herbarts, durchaus keine
Vorarbeiten benutzen konnte.
[pag. 3]
I.
Größenbegriffe sind nur da möglich,
wo sich ein allgemeiner Begriff vorfindet, der verschiedene Bestimmungsweisen
zuläßt. Je nachdem unter diesen Bestimmungsweisen von einer zu
einer andern ein stetiger Übergang stattfindet oder nicht, bilden sie eine
stetige oder diskrete Mannigfaltigkeit; die einzelnen Bestimmungsweisen
heißen im erstern Falle Punkte, im letztern Elemente dieser
Mannigfaltigkeit. Begriffe, deren Bestimmungsweisen eine diskrete
Mannigfaltigkeit bilden, sind so häufig, daß sich für beliebig
gegebene Dinge wenigstens in den gebildeteren Sprachen immer ein Begriff
ausfinden läßt, unter welchem sie enthalten sind (und die
Mathematiker konnten daher in der Lehre von den diskreten Größen
unbedenklich von der Forderung ausgehen, gegebene Dinge als gleichartig zu
betrachten), dagegen sind die Veranlassungen zur Bildung von Begriffen, deren
Bestimmungsweisen eine stetige Mannigfaltigkeit bilden, im gemeinen Leben so
selten, daß die Orte der Sinnengegenstände und die Farben wohl
die einzigen einfachen Begriffe sind, deren Bestimmungsweisen eine mehrfach
ausgedehnte Mannigfaltigkeit bilden. Häufigere Veranlassung zur
Erzeugung und Ausbildung dieser Begriffe findet sich erst in der höheren
Mathematik.
Bestimmte, durch ein Merkmal oder eine Grenze
unterschiedene Teile einer Mannigfaltigkeit heißen Quanta. Ihre
Vergleichung der Quantität nach geschieht bei den diskreten
Größen durch Zählung, bei den stetigen durch Messung. Das
Messen besteht in einem Aufeinanderlegen der zu vergleichende
Größen; zum Messen wird also ein Mittel erfordert, die eine
Größe als Maßstab für die andere forzutragen. Fehl
dieses, so kann man zwei Größen nur vergleichen, wenn die eine
ein Teil der andern ist, und auch dann nur als Mehr
[pag. 4]
oder Minder, nicht das Wieviel entscheiden. Die Untersuchungen, welche sich in
diesem Falle über sie anstellen lassen, bilden einen allgemeinen von
Maßbestimmungen unabhängigen Teil der Größenlehre,
wo die Größen nicht als unabhängig von der Lage existierend
und nicht als durch eine Einheit ausdrückbar, sondern als Gebiete in einer
Mannigfaltigkeit betrachtet werden. Solche Untersuchungen sind für
mehrere Teile der Mathematik, namentlich für die Behandlung der
mehrwertigen analytischen Funktionen ein Bedürfnis geworden, und der
Mangel derselben ist wohl ein Hauptursache, daß der berühmte
Abelsche Satz und die Leistungen von Lagrange, Pfaff, Jacobi für die
allgemeine Theorie der Differentialgleichungen solange unfruchtbar geblieben
sind. Für den gegenwärtigen Zweck genügt es, aus diesem
allgemeinen Teile der Lehre von den ausgedehnten Größen, wo
weiter nichts vorausgesetzt wird, als was in dem Begriffe derselben schon
erhalten ist, zwei Punkte hervorzuheben, wovon der erste die Erzeugung des
Begriffs einer mehrfach ausgedehnten Mannigfaltigkeit, der zweite die
Zurückführung der Ortsbestimmungen in einer gegebenen
Mannigfaltigkeit auf Quantitätsbestimmungen betrifft und das wesentliche
Kennzeichen einer n-fachen Ausdehnung deutlich machen
wird.
2.
Geht man bei einem Begriffe, dessen
Bestimmungsweisen eine stetige Mannigfaltigkeit bilden, von einer
Bestimmungsweise auf eine bestimmte Art zu einer andern über, so
bilden die durchlaufenden Bestimmungsweisen eine einfach ausgedehnte
Mannigfaltigkeit, deren wesentliches Kennzeichen ist, daß in ihr von
einem Punkt nur nach zwei Seiten, vorwärts oder rückwärts,
ein stetiger Fortgang möglich ist. Denkt man sich nun, daß diese
Mannigfaltigkeit
[pag. 5]
wieder in eine andere, völlig verschiedene, übergeht, und zwar
wieder auf bestimmte Art, d.h. so, daß jeder Punkt in einen bestimmten
Punkt der andern übergeht, so bilden sämtliche so erhaltene
Bestimmungsweisen eine zweifach ausgedehnte Mannigfaltigkeit. In
ähnlicher Weise erhält man eine dreifach ausgedehnte
Mannigfaltigkeit, wenn man sich vorstellt, daß eine zweifach ausgedehnte
in eine völlig verschiedene auf bestimmte Art übergeht, und es ist
leicht zu sehen, wie man diese Konstruktion fortsetzen kann. Wenn man,
anstatt den Begriff als bestimmbar, seinen Gegenstand als veränderlich
betrachtet, so kann diese Konstruktion bezeichnet werden als eine
Zusammensetzung einer Veränderlichkeit von n + 1
Dimensionen aus einer Veränderlichkeit von n Dimensionen und
aus einer Veränderlichkeit von Einer Dimension.
3.
Ich werde nun zeigen, wie man umgekehrt eine
Veränderlichkeit deren Gebiet gegeben ist, in eine Veränderlichkeit
von einer Dimension und eine Veränderlichkeit von weniger Dimensionen
zerlegen kann. Zu diesem Ende denke man sich ein veränderliches
Stück einer Mannigfaltigkeit von Einer Diemnsion -- von einem festen
Anfangspunkt an gerechnet, so daß die Werte desselben untereinander
vergleichbar sind --, welches für jeden Punkt der gegebenen
Mannigfaltigkeit einen bestimmten mit ihm stetig sich ändernden Wert
hat, oder mit andern Worten, man nehme innerhalb der gegebenen
Mannigfaltigkeit eine stetige Funktion des Orts an, und zwar eine solche
Funktion, welche nich längs eines Teils dieser Mannigfaltigkeit konstant
ist. Jedes System von Punkten, wo die Funktion einen konstanten Wert hat,
bildet dann eine stetige Mannigfaltigkeit von weniger Dimensionen als die
gegebene. Diese Mannigfaltigkeiten
[pag. 6]
gehen bei Änderung der Funktion stetig ineinander über; man wird
daher annehmen können, daß aus einer von ihnen die übrigen
hervorgehen, und es wird dies, allgemein zu reden, so geschehen können,
daß jeder Punkt in einen bestimmten Punkt der andern übergeht; die
Ausnahmsfälle, deren Untersuchung wichtig ist, können hier
unberücksichtigt bleiben. Hierdurch wird die Ortsbestimmung in der
gegebenen Mannigfaltigkeit zurückgeführt auf eine
Größenbestimmung und auf eine Ortsbestimmung in einer
minderfach ausgedehnten Mannigfaltigkeit. Es ist nun leicht zu zeigen,
daß die gegebene Mannigfaltigkeit n - 1 Dimensionen hat,
wenn die gegebene Mannigfaltigkeit eine n-fach ausgedehnte ist.
Durch n-malige Wiederholung dieses Verfahrens wird daher die
Ortsbestimmung in einer n-fach ausgedehnten Mannigfalitgkeit auf
n Größenbestimmungen, und also die Ortsbestimmung in
einer gegebenen Mannigfaltigkeit, wenn dieses möglich ist, auf eine
endliche Anzahl von Qualitätsbestimmungen zurückgeführt. Es
gibt indes auch Mannigfaltigkeiten, in welchen die Ortsbestimmung nicht eine
endliche Zahl, sondern entweder eine unendliche Reihe oder eine stetige
Mannigfaltigkeit von Größenbestimmungen erfordert. Solche
Mannigfaltigkeiten bilden z.B. die mögliche Bestimmungen einer Funktiom
für ein gegebenes Gebiet, die möglichen Gestalten einer
räumlichen Figur usw.
II. Maßverhältnisse, deren eine Mannigfaltigkeit von
n Di-
mensionen fähig ist, unter der Voraussetzung, daß die
Linien unabhängig von der Lage eine länge besitzen, also
jede Linie durch jede meßbar ist.
Es folgt nun, nachdem der Begriff einer
n-fach ausgedehnten Mannigfaltigkeit konstruirt und als wesentliches
Kennzeichen derselben gefunden worden ist, daß sich die
[pag. 7]
Ortsbestimmung in derselben auf n Größenbestimmungen
zurückführen läßt, als zweite der oben gestellten
Aufgaben eine Untersuchung über die Maßverhältnisse, deren
eine solche Mannigfaltigkeit fähig ist, und über die Bedingungen,
welche zur Bestimmung dieser Maßverhältnisse hinreichen. Diese
Maßverhältnisse lassen sich nur in abstrakten
Größenbegriffen untersuchen und im Zusammenhange nur durch
Formeln darstellen; unter gewissen Voraussetzungen kann man sie indes in
Verhältnisse zerlegen, welche einzeln genommen einer geometrischen
Darstellung fähig sind, und hierdurch wird es möglich, die Resultate
der Rechnung geometrisch auszudrücken. Es wird daher, um festen Boden
zu gewinnen, zwar eine abstrakte Untersuchung in Formeln nicht zu vermeiden
sein, die Resultate derselben aber werden sich im geometrischen Gewanden
dartsellen lassen. Zu beidem sind die Grundlagen enthalten in der
berühmten Abhandlung der Herrn Geheimen Hofrats Gauß
über die krummen Flächen.
1.
Maßbestimmungen erfordern eine
Unabhängigkeit der Größen vom Ort, die in mehr als einer
Weise stattfinden kann; die zunächst sich darbietende Annahme, welche
ich hier verfolgen will, ist wohl die, daß die Länge der Linien
unabhängig von der Lage sei, also jede Linie durch jede meßbar sei.
Wird die Ortsbestimmung auf Größenbestimmungen
zurückgeführt, also die Lage eines Punktes in der gegegeben
n-fach ausgedehnten Mannigfaltigkeit durch n
veränderliche Größen x1,
x2, x3 und so fort bis
xn ausgedrückt, so wird dir
Bestimmung einer Linie darauf hinauskommen, daß die
Größem x als Funktionen Einer Veränderlichen
gegeben werden. Die Aufgabe ist dann, für die Länge der Linien
einen mathematischen Ausdruck aufzustellen, ze welchem Zwecke die
Größen x als in Einheiten ausdrückbar betrachtet
werden
[pag. 8]
müssen. Ich werde diese Aufgabe nur unter gewissen
Beschränkungen behandeln und beschränke mich erstlich auf solche
Linien, in welchen die Verhältnisse zwischen den Größen
dx -- den zusammengehörigen Änderungen der
Größen x -- sich stetig ändern; man kann dann die
Linien in Elemente zerlegt denken, innerhalb deren die Verhältnisse der
Größen dx als konstant betrachtet werden dürfen,
und die Aufgabe kommt dann darauf zurück, für jeden Punkt einen
allgemeinen Ausdruck des von ihm ausgehenden Linienelements ds
aufzustellen, welcher also die Größen x und die
Größen dx enthalten wird. Ich nehme nun zweitens an,
daß die Länge des Linienelements, von Größen zweiter
Ordnung abgesehen, ungeändert bleibt, wenn sämtliche Punkte
desselben dieselbe unendlich kleine Ortänderung erleiden, worin zugleich
enthalten ist, daß, wenn sämtliche Größen
dx im demselben Verhältnisse wachsen, das Linienelement sich
ebenfalls in diesem Verhältnisse ändert. Unter diesen Annahmen
wird das Linienelement eine beliebige homogene FUnktion ersten Grades der
Größen dx sein können, welche ungeändert
bleibt, wenn sämtliche Größen dx ihr Zeichen
ändern, und worin die willkürlichen Konstanten stetige Funktionen
der Größen x sind. Um die einfachsten Fälle zu
finden, suche ich zunächst einen Ausdruck für die
(n - 1)-fach ausgedehnten Mannigfaltigkeiten, welche vom
Anfangspunkte des Linienelements überall gleich weit abstehen, d.h. ich
suche eine stetige Funktion des Orts, welche sie voneinander unterscheidet.
Diese wird vom Anfangspunkt aus nach allen Seiten entweder ab- oder
zunehmen müssen; ich will annehmen, daß sie nach allen Seiten
zunimmt und also in dem Punkte ein Minimum hat. Es muß dann, wenn
ihre ersten und zweiten Differentialquotienten endlich sind, das Differential
erster Ordnung verschwinden und das zweiter Ordnung darf nie negativ werden;
ich nehme an, daß es
[pag. 9]
immer positiv bleibt. Dieser Differentialausdruck zweiter Ordnung bleibt alsdann
konstannt, wenn ds konstant bleibt, und wächst im
quadratischen Verhältnisse, wenn die Größen dx
und also auch ds sich sämtlich in demselben Verhältnisse
ändern; er ist also gleich const · ds2,
und folglich ist ds gleich der Quadratwurzel aus einer immer positiven
ganzen homogenen Funktion zweiten Grades der Größen
dx, in welcher die Koeffizienten stetige Funktionen der
Größen x sind. Für den Raum wird, wenn man die
Lage der Punkte durch rechtwinklige Koordinaten ausdrückt, ds
= 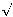
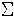 (dx)2); der Raum ist also unter diesem einfachsten
Falle enthalten. Der nächst einfache Fall würde wohl die
Mannigfaltigkeiten umfassen, in welchen sich das Linienelement durch die vierte
Wurzel aus einem Differentialausdrucke vierten Grades ausdrücken
läßt. Die Untersuchung dieser allgemeinern Gattung würde
zwar keine wesentlich andere Prinzipien erfordern, aber ziemlich zeitraubend sein
und verhältnismäßig auf die Lehre vom Raume wenig neues
Licht werfen, zumal da sich die Resultate nicht geometrisch ausdrücken
lassen; ich beschränke mich daher auf die Mannigfaltigkeiten, wo das
Linienelement durch die Quadratwurzel aus einem Differentialausdruck zweiten
Grades ausgedrückt wird. Man kann einen solchen Ausdruck in einen
andern ähnlichen transformieren, indem man für die n
unabhängigen Veränderlichen Funktionen von n neuen
unabhängigen Veränderlichen setzt. Auf diesem Wege wird man
aber nicht jeden Ausdruck in jeden transformieren können; denn der
Ausdruck enthält n(n + 1)/2 Koeffizienten, welche
willkürliche Funktionen der unabhängigen Veränderlichen sind;
durch Einführung neuer Veränderlichen wird man aber nur
n Relationen genügen und also nur n der
Koeffizienten gegebenen Größen gleich machen können. Es
sind dann die übrigen n(n - 1)/2
[pag. 10]
durch die Natur der darzustellenden Mannigfaltigkeit schon völlig
bestimmt, und zur Bestimmung ihrer Maßverhältnisse also
n(n - 1)/2 Funktionen des Orts erforderlich. Die
Mannigfaltigkeiten, in welchen sich, wie in der Ebene und im Raume, das
Linienelement auf die Form
(dx)2); der Raum ist also unter diesem einfachsten
Falle enthalten. Der nächst einfache Fall würde wohl die
Mannigfaltigkeiten umfassen, in welchen sich das Linienelement durch die vierte
Wurzel aus einem Differentialausdrucke vierten Grades ausdrücken
läßt. Die Untersuchung dieser allgemeinern Gattung würde
zwar keine wesentlich andere Prinzipien erfordern, aber ziemlich zeitraubend sein
und verhältnismäßig auf die Lehre vom Raume wenig neues
Licht werfen, zumal da sich die Resultate nicht geometrisch ausdrücken
lassen; ich beschränke mich daher auf die Mannigfaltigkeiten, wo das
Linienelement durch die Quadratwurzel aus einem Differentialausdruck zweiten
Grades ausgedrückt wird. Man kann einen solchen Ausdruck in einen
andern ähnlichen transformieren, indem man für die n
unabhängigen Veränderlichen Funktionen von n neuen
unabhängigen Veränderlichen setzt. Auf diesem Wege wird man
aber nicht jeden Ausdruck in jeden transformieren können; denn der
Ausdruck enthält n(n + 1)/2 Koeffizienten, welche
willkürliche Funktionen der unabhängigen Veränderlichen sind;
durch Einführung neuer Veränderlichen wird man aber nur
n Relationen genügen und also nur n der
Koeffizienten gegebenen Größen gleich machen können. Es
sind dann die übrigen n(n - 1)/2
[pag. 10]
durch die Natur der darzustellenden Mannigfaltigkeit schon völlig
bestimmt, und zur Bestimmung ihrer Maßverhältnisse also
n(n - 1)/2 Funktionen des Orts erforderlich. Die
Mannigfaltigkeiten, in welchen sich, wie in der Ebene und im Raume, das
Linienelement auf die Form 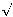
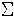 dx2
bringen läßt, bilden daher nur einen besonderen Fall der hier zu
untersuchenden Mannigfaltigkeiten; sie verdienen wohl einen besonderen
Namen, und ich will also diese Mannigfaltigkeiten, in welchen sich das Quadrat
des Linienelements auf die Summe der Quadrate von selbständigen
Differentialien bringen läßt, eben nennen. Um nun die wesentlichen
Verschiedenheiten sämlicher in der vorausgesetzten Form darstellbarer
Mannigfaltigkeiten übersehen zu können, ist es nötig, die von
der Darstellungsweise herrührenden zu beseitigen, was durch die Wahl der
verändelichen Größen nach einem bestimmten Prinzip erreicht
wird.
dx2
bringen läßt, bilden daher nur einen besonderen Fall der hier zu
untersuchenden Mannigfaltigkeiten; sie verdienen wohl einen besonderen
Namen, und ich will also diese Mannigfaltigkeiten, in welchen sich das Quadrat
des Linienelements auf die Summe der Quadrate von selbständigen
Differentialien bringen läßt, eben nennen. Um nun die wesentlichen
Verschiedenheiten sämlicher in der vorausgesetzten Form darstellbarer
Mannigfaltigkeiten übersehen zu können, ist es nötig, die von
der Darstellungsweise herrührenden zu beseitigen, was durch die Wahl der
verändelichen Größen nach einem bestimmten Prinzip erreicht
wird.
2.
Zu diesem Ende denke man sich von einem beliebigen
Punkte aus das System der von ihm ausgehenden kürzesten Linien
konstruiert; die Lage eines unbestimmten Punktes wird dann bestimmt werden
können durch die Anfangsrichtung der kürzesten Linie, in welcher er
liegt, und durch seine Entfernung in dersleben vom Anfangspunkte und kann
daher durch die Verhältnisse der Grösse
dx0, d.h. die Länge s dieser Linie
ausgedrückt werden. Man führe nun statt
dx0 solche aus ihnen gebildete lineare
Ausdrücke d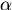 ein,
daß der Anfangswert des Quadrats des Linienelements gleich der Summe
der Quadrate dieser Ausdrücke wird, so daß die unabhängigen
Variabeln sind: die Größe s und die Verhältnisse der
Größen d
ein,
daß der Anfangswert des Quadrats des Linienelements gleich der Summe
der Quadrate dieser Ausdrücke wird, so daß die unabhängigen
Variabeln sind: die Größe s und die Verhältnisse der
Größen d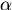 ;
und setze schließlich statt
d
;
und setze schließlich statt
d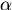 [pag. 11]
solche ihnen proportionale Größen x1,
x2, . . ., xn,
daß die Quadratsumme gleich s2 wird.
Führt man diese Größen ein, so wird für unendlich
kleine Werte von x das Quadrat des Linienelements gleich
[pag. 11]
solche ihnen proportionale Größen x1,
x2, . . ., xn,
daß die Quadratsumme gleich s2 wird.
Führt man diese Größen ein, so wird für unendlich
kleine Werte von x das Quadrat des Linienelements gleich
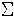 dx2,
das Glied der nächsten Ordnung in demselben aber gleich einem
homogenen Ausdruck zweiten Grades der n(n - 1)/2
Größen
(x1dx2 -
x2dx1),
(x1dx3 -
x3dx1), . . ., also eine
unendlich kleine Größe von der vierten Dimension, so daß
man eine unendlich Größe erhält, wenn man sie durch das
Quadrat des unendlich kleinen Dreiecks dividiert, in dessen Eckpunkten die
Werte der Veränderlichen sind (0, 0, 0, . . .),
(x1, x2,
x3, . . .), (dx1,
dx2, dx3, . . .). Diese
Größe behält denselben Wert, solange die Größen
x und dx in denselben binären Linearformen enthalten
sind, oder solange die beiden kürzesten Linien von den Werten 0 bis zu
den Werten x und von den Werten 0 bis zu den Werten dx
in demselben Flächenelement bleiben, und hängt also nur von Ort
und Richtung desselben ab. Sie wird offenbar = 0, wenn die dargestellte
Mannigfaltigkeit eben, d.h. das Quadrat des Linienelements auf
dx2,
das Glied der nächsten Ordnung in demselben aber gleich einem
homogenen Ausdruck zweiten Grades der n(n - 1)/2
Größen
(x1dx2 -
x2dx1),
(x1dx3 -
x3dx1), . . ., also eine
unendlich kleine Größe von der vierten Dimension, so daß
man eine unendlich Größe erhält, wenn man sie durch das
Quadrat des unendlich kleinen Dreiecks dividiert, in dessen Eckpunkten die
Werte der Veränderlichen sind (0, 0, 0, . . .),
(x1, x2,
x3, . . .), (dx1,
dx2, dx3, . . .). Diese
Größe behält denselben Wert, solange die Größen
x und dx in denselben binären Linearformen enthalten
sind, oder solange die beiden kürzesten Linien von den Werten 0 bis zu
den Werten x und von den Werten 0 bis zu den Werten dx
in demselben Flächenelement bleiben, und hängt also nur von Ort
und Richtung desselben ab. Sie wird offenbar = 0, wenn die dargestellte
Mannigfaltigkeit eben, d.h. das Quadrat des Linienelements auf
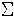 dx2
reduzierbar ist, und kann daher als das Maß der in diesem Punkte in
dieser Flächenrichtung stattfindenden Abweichung der Mannigfaltigkeit
von der Ebenheit angesehen werden. Multipliziert mit
-3/4 wird sie der Größe gleich,
welche Herr Geheimer Hofrat Gauß das Krümmungsmaß einer
Fläche genannt hat. Zur Bestimmung der Maßverhältnisse
einer n-fach ausgedehnhten, in der voausgesetzten Form darstellbaren
Mannigfaltigkeit wurden vorhin n(n - 1)/2 Funktionen des
Orts nötig gefunden; wenn also das Krümmungsmaß in jedem
Punkte in n(n - 1)/2 Flächenrichtungen gegeben wird,
so werden daraus die Maßverhältnisse der Mannigfaltigkeit sich
bestimmen lassen,
[pag. 12]
wofern nur zwischen diesen Werten keine identischen Relationen
stattfinden, was in der Tat, allgemein zu reden, nicht
der Fall ist. Die Maßverhältnisse dieser Mannigfaltigkeiten,
wo das Linienelement durch die Quadratwurzel aus einem
Differentialausdruck zweiten Grades dargestellt wird, lassen
sich so auf eine von der Wahl der veränderlichen Größen
völlig unabhängige Weise ausdrücken. Ein ganz ähnlicher
Weg läßt sich zu diesem Ziele auch bei den Mannigfaltigkeiten
einschlagen, in welchen das Linienelement durch einen
weniger einfachen Ausdruck, z.B. durch die vierte Wurzel
aus einem Differentialausdruck vierten Grades, ausgedrückt
wird. Es würde sich dann das Linienelement, allgemein zu
reden, nicht mehr auf die Form der Quadratwurzel aus einer
Quadratsumme von Differentialausdrücken bringen lassen
und also in dem Ausdrucke für das Quadrat des Linienelements
die Abweichung von der Ebenheit eine unendlich
kleine Größe von der zweiten Dimension sein, während sie
bei jenen Mannigfaltigkeiten eine unendlich kleine Größe
von der vierten Dimension war. Diese Eigentümlichkeit
der letztern Mannigfaltigkeiten kann daher wohl Ebenheit
in den kleinsten Teilen genannt werden. Die für den jetzigen
Zweck wichtigste Eigentümlichkeit dieser Mannigfaltigkeiten,
derentwegen sie hier allein untersucht worden sind, ist aber
die, daß sich die Verhältnisse der zweifach ausgedehnten
geometrisch durch Flächen darstellen und die der mehrfach
ausgedehnten auf die der in ihnen enthalteten Flächen
zurückführen lassen, was jetzt noch einer kurzen Erörterung
bedarf.
dx2
reduzierbar ist, und kann daher als das Maß der in diesem Punkte in
dieser Flächenrichtung stattfindenden Abweichung der Mannigfaltigkeit
von der Ebenheit angesehen werden. Multipliziert mit
-3/4 wird sie der Größe gleich,
welche Herr Geheimer Hofrat Gauß das Krümmungsmaß einer
Fläche genannt hat. Zur Bestimmung der Maßverhältnisse
einer n-fach ausgedehnhten, in der voausgesetzten Form darstellbaren
Mannigfaltigkeit wurden vorhin n(n - 1)/2 Funktionen des
Orts nötig gefunden; wenn also das Krümmungsmaß in jedem
Punkte in n(n - 1)/2 Flächenrichtungen gegeben wird,
so werden daraus die Maßverhältnisse der Mannigfaltigkeit sich
bestimmen lassen,
[pag. 12]
wofern nur zwischen diesen Werten keine identischen Relationen
stattfinden, was in der Tat, allgemein zu reden, nicht
der Fall ist. Die Maßverhältnisse dieser Mannigfaltigkeiten,
wo das Linienelement durch die Quadratwurzel aus einem
Differentialausdruck zweiten Grades dargestellt wird, lassen
sich so auf eine von der Wahl der veränderlichen Größen
völlig unabhängige Weise ausdrücken. Ein ganz ähnlicher
Weg läßt sich zu diesem Ziele auch bei den Mannigfaltigkeiten
einschlagen, in welchen das Linienelement durch einen
weniger einfachen Ausdruck, z.B. durch die vierte Wurzel
aus einem Differentialausdruck vierten Grades, ausgedrückt
wird. Es würde sich dann das Linienelement, allgemein zu
reden, nicht mehr auf die Form der Quadratwurzel aus einer
Quadratsumme von Differentialausdrücken bringen lassen
und also in dem Ausdrucke für das Quadrat des Linienelements
die Abweichung von der Ebenheit eine unendlich
kleine Größe von der zweiten Dimension sein, während sie
bei jenen Mannigfaltigkeiten eine unendlich kleine Größe
von der vierten Dimension war. Diese Eigentümlichkeit
der letztern Mannigfaltigkeiten kann daher wohl Ebenheit
in den kleinsten Teilen genannt werden. Die für den jetzigen
Zweck wichtigste Eigentümlichkeit dieser Mannigfaltigkeiten,
derentwegen sie hier allein untersucht worden sind, ist aber
die, daß sich die Verhältnisse der zweifach ausgedehnten
geometrisch durch Flächen darstellen und die der mehrfach
ausgedehnten auf die der in ihnen enthalteten Flächen
zurückführen lassen, was jetzt noch einer kurzen Erörterung
bedarf.
3.
In die Auffassung der Flächen mischt sich neben
den inneren Maßverhältnissen, bei welchen nur die Länge der
Wege in ihnen in Betracht kommt, immer auch ihre Lage
zu außer ihnen gelegenen Punkten. Man kann aber von
[pag. 13]
den äußeren Verhältnisse abstrahieren, indem man solche
Veränderungen mit ihnen vornimmt, bei denen die Länge
der Linien in ihnen ungeändert bleibt, d.h. sie sich beliebig
-- ohne Dehnung -- gebogen denkt, und alle so auseinander
entstehenden Flächen als gleichartig betrachtet. Es gelten
also z.B. beliebige zylindrische oder konische Flächen einer
Ebene gleich, weil sie sich durch bloße Biegung aus ihr
bilden lassen, wobei die inneren Maßverhältnisse bleiben,
und sämtliche Sätze über dieselben -- also die ganze
Planimetrie -- ihre Gültigkeit behalten; dagegen gelten sie als
wesentlich verschieden von der Kugel, welche sie nicht ohne
Dehnung in eine Ebene verwandeln läßt. Nach der vorigen
Untersuchung werden in jedem Punkte die inneren Maßverhältnisse
einer zweifach ausgedehnten Größe, wenn sich
das Linienelement durch die Quadratwurzel aus einem
Differentialausdruck zweiten Grades ausdrücken läßt, wie
dies bei den Flächen der Fall ist, charakterisiert durch das
Krümmungsmaß. Dieser Größe läßt sich
nun bei den Flächen
die anschauliche Bedeutung geben, daß sie das Produkt aus
den beiden Krümmungen der Fläche in diesem Punkte ist,
oder auch, daß das Produkt derselben in eine unendlich kleines
aus kürzesten Linien gebildetes Dreieck gleich ist dem Überschlusse
seiner Winkelsumme über zwei Rechte in Teilen des
Halbmessers. Die erste Definition würde den Satz voraussetzen,
daß das Produkt der beiden Krümmungshalbmesser
bei der bloßen Biegung einer Fläche ungeändert bleibt, die
zweite, daß an demselben Orte der Überschuß der
Winkelsumme eines unendlich kleinen Dreiecks über zwei Rechte
seinem Inhalte proportional ist. Um dem Krümmungsmaß
einen n-fach ausgedehnten Mannigfaltigkeit in einem gegebenen
Punkte und einer gegebenen durch ihn gelegten
Flächenrichtung eine greifbare Bedeutung zu geben, muß
man davon ausgehen, daß eine von einem Punkte ausgehende
[pag. 14]
kürzeste Linie völlig bestimmt ist, wenn ihre Anfangsrichtung
gegeben ist. Hiernach wird man eine bestimmte Fläche erhalten,
wenn man sämtliche von dem gegebenen Punkte ausgehenden
und in dem gegebenen Flächenelement liegenden
Anfangsrichtungen zu kürzesten Linien verlängert, und diese
Fläche hat in dem gegebenen Punkte ein bestimmtes
Krümmungsmaß, welches zugleich das Krümmungsmaß
der n-fach ausgedehnten Mannigfaltigkeit in dem gegebenen Punkte
und der gegebenen Flächenrichtung ist.
4.
Es sind nun noch, ehe die Anwendung auf den Raum
gemacht wird, einige Betrachtungen über die ebenen Mannigfaltigkeiten
im allgemeinen nötig, d.h. über diejenigen in
welchen das Quadrat des Linienelement durch eine Quadratsumme
vollständiger Differentialen darstelbar ist.
In einer ebenen n-fach ausgedehnten
Mannigfaltigkeit ist das Krümmungsmaß in jedem Punkte in jeder
Richtung Null; es reicht aber nach der frühern Untersuchung, um
die Maßverhältnisse zu bestimmen, hin, zu wissen, daß es
in jedem Punkte in n·(n - 1)/2
Flächenrichtungen, deren
Krümmungsmaße voneinander unabhängig sind, Null sei.
Die Mannigfaltigkeiten, deren Krümmungsmaß überall = 0
ist, lassen sich betrachten als ein besonderer Fall derjenigen
Mannigfaltigkeiten, deren Krümmungsmaß allenthalben konstant
ist. Der gemeinsame Charakter dieser Mannigfaltigkeiten,
deren Krümmungsmaß konstant is, kann auch so
ausgedrückt werden, daß sich die Figuren in ihnen ohne
Dehnung bewegen lassen. Denn offenbar würden die Figuren
in ihnen nicht beliebig verschiebbar und drehbar sein können,
wenn nicht in jedem Punkte in allen Richtungen das
Krümmungsmaß dasselbe wäre. Andererseits aber sind durch
das [pag. 15]
Krümmungsmaß die Maßverhältnisse der
Mannigfaltigkeit vollständig bestimmt; es sind daher um einen Punkt nach
allen Richtungen die Maßverhältnisse genau dieselben, wie
um einen andern, und also von uhm aus dieselben Konstruktionen
ausführbar, und folglich kann in den Mannigfaltigkeiten
mit konstantem Krümmungsmaß den Figuren jede
beliebige Lage gegeben werden. Die Maßverhältnisse dieser
Mannigfaltigkeiten hängen nur von dem Werte des
Krümmungsmaßes ab, und in bezug auf die die analytische
Darstellung mag bemerkt werden, daß, wenn man diesen Wert
durch 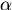 bezeichnet,
dem Ausdruck für das Linienelement die Form
bezeichnet,
dem Ausdruck für das Linienelement die Form
 gegeben werden kann.
gegeben werden kann.
5.
Zur geometrischen Erläuterung kann die
Betrachtung der Flächen mit konstantem Krümmungsmaß
dienen. Es ist leicht zu sehen, daß sich die Flächen, deren
Krümmungsmaß positiv ist, immer auf eine Kugel, deren Radius
gleich 1 dividiert durch die Wurzel aus dem Krümmungsmaß ist,
wickeln lassen werden; um aber die ganze Mannigfaltigkeit
dieser Flächen zu übersehen, gebe man einer derselben die
Gestalt einer Kugel und den übrigen die Gestalt von
Umdrehungsflächen, welche sie im Äquator berühren. Die
Flächen mit größerem Krümmungsmaß als diese
Kugel werden dann die Kugel von innen berühren und eine Gestalt
annehmen, wie der äußere der Achse abgewandte Teil der
Oberfläche eines Ringes; sie würden sich auf Zonen von
Kugeln mit kleinerem Halbmesser wickeln lassen, aber mehr
als einmal herumreichen. Die Flächen mit kleinerem positiven
[pag. 16]
Krümmungsmaß wird man erhalten, wenn man aus
Kugelflächen mit größerem Radius ein von zwei
größten Halbkreisen begrenztes Stück ausschneidet und die
Schnittlinien zusammenfügt. Die Fläche mit dem
Krümmungsmaß Null wird eine auf dem Äquator stehende
Zylinderfläche sein; die Flächen mit negativem
Krümmungsmaß aber werden diesen Zylinder von außen
berühren und wie der innere
des Achse zugewandte Teil der Oberfläche eines Ringes
geformt sein. Denkt man diese Flächen als Ort für in
ihnen bewegliche Flächenstücke, wie den Raum als Ort
für Körper, so sind in allen diesen Flächen die
Flächenstücke ohne Dehnung beweglich. Die Flächen mit
positivem Krümmungsmaß lassen sich stets so formen, daß
die Flächenstücke auch ohne Biegung beliebig bewegt werden
können, nämlich zu Kugelflächen, die mit negativem aber
nicht. Außer dieser Unabhängigkeit der Flächenstücke
vom Ort findet bei der Fläche mit dem Krümmungsmaß Null
auch eine Unabhängigkeit der Richtung vom Ort statt, welche bei
den übrigen Flächen nicht stattfindet.
III. Anwendung auf den Raum.
1.
Nach diesen Untersuchungen über die
Bestimmung der Maßverhältnisse einer n-fach
ausgedehnten Größe lassen sich nun die Bedingungen angeben,
wlche zur Bestimmung der Maßverhältnisse des Raumes
hinreichend und notwendig sind, wenn Unabhängigkeit der Linien von der
Lage und Darstellbarkeit das Linienelements durch die Quadratwurzel
aus einem Differentialausdrucke zweiten Grades, also Ebenheit
in den kleinsten Teilen vorausgesetzt wird.
Sie lassen sich erstens so ausdrücken, daß
das Krümmungsmaß in jedem Punkte in drei
Flächenrichtungen = 0
[pag. 17]
ist, und es sind daher die Maßverhältnisse des Raumes
bestimmt, wenn die Winkelsumme im Dreieck allenthalben
gleich zwei Rechten ist.
Setzt man aber zweitens, wie Euklid, nicht bloß
eine von der Lage unabhängige Existenz der Linien, sondern auch
der Körper voraus, so folgt, daß das Krümmungsmaß
allenthalben konstant ist, und es ist dann in allen Dreiecken
die Winkelsumme bestimmt, wenn sie in Einem bestimmt ist.
Endlich könnte man drittens, anstatt die
Länge der Linien als unabhängig von Ort und Richtung anzunehmen,
auch eine Unabhängigkeit ihrer Länge und Richtung vom
Ort voraussetzen. Nach dieser Auffassung sind die Ortsänderungen
oder Ortsverschiedenheiten komplexe, in drei
unabhängigen Einheiten ausdrückbare Größen.
2.
Im Laufe der bisherigen Betrachtungen wurden
zunächst die Ausdehnungs- oder Gebietsverhältnisse von den
Maßverhältnissen gesondert und gefunden, daß bei
denselben Ausdehnungsverhältnissen verschiedene
Maßverhältnisse denkbar sind; es wurden dann die Systeme
einfacher Maßbestimmungen aufgesucht, durch welche die
Maßverhältnisse des Raumes völlig bestimmt sind und von
welchem alle Sätze über dieselben eine notwendige Folge sind; es
bleibt nun die Frage zu erörtern, wie, in welchem Grade und in welchem
Umfange diese Voraussetzungen durch die Erfahrung verbürgt
werden. In dieser Beziehung findet zwischen den
bloßen Ausdehnungsverhältnisse und den
Maßverhältnissen eine wesentliche Verschiedenheit statt, insofern
bei erstern, wo die möglichen Fälle eine diskrete Mannigfaltigkeit
bilden, die Aussagen der Erfahrung zwar nie völlig gewiß, aber nicht
ungenau sind, während bei letztern, wo die möglichen Fälle
eine stetige Mannigfaltigkeit bilden, jede Bestimmung aus
[pag. 18]
der Erfahrung immer ungenau bleibt -- es mag die Wahrscheinlichkeit,
daß sie nahe richtig ist, noch so groß sein.
Dieser Umstand wird wichtig bei der Ausdehnung dieser empirischen
Bestimmungen über die Grenzen der Beobachtung
ins Unmeßbargroße und Unmeßbarkleine; denn die
letztern können offenbar jenseits der Grenzen der Beobachtung
immer ungenauer, die ersteren aber nicht.
Bei der Ausdehnung der Raumkonstruktionen ins
Unmeßbargroße ist Unbegrenztheit und Unendlichkeit zu scheiden;
jene gehört zu den Ausdehnungsverhältnissen, diese zu
den Maßverhältnissen. Daß der Raum eine unbegrenzte
dreifach ausgedehnte Mannigfaltigkeit sei, ist eine Voraussetzung,
welche bei jeder Auffassung der Außenwelt angewandt wird,
nach welcher in jedem Augenblicke das Gebiet der wirklichen
Wahrnehmungen ergänzt und die möglichen Orte eines
gesuchten Gegenstandes konstruiert werden und welche sich
bei diesen Anwendungen fortwährend bestätigt. Die
Unbegrenztheit des Raumes besitzt daher eine größere empirische
Gewißheit als irgendeine äußere Erfahrung. Hieraus folgt
aber die Unendlichkeit keineswegs; vielmehr würde der
Raum, wenn man Unabhängigkeit der Körper vom Ort
voraussetzt, ihm also ein konstantes Krümmungsmaß zuschreibt,
notwendig endlich sein, sobald dieses Krümmungsmaß
einen noch so kleinen positiven Wert hätte. Man würde,
wenn man die in einem Flächenelement liegenden Anfangsrichtungen
zu kürzesten Linien verlängert, eine unbegrenzte
Fläche mit konstantem positiven Krümmungsmaß, also eine
Fläche erhalten, welche in einer ebenen dreifach ausgedehnten
Mannigfaltigkeit die Gestalt einer Kugelfläche annehmen
würde und welche folglich endlich ist.
[pag. 19]
3.
Die Fragen über das Unmeßbargroße
sind für die Naturerklärung müßige Fragen. Anders
verhält es sich aber mit den Fragen über das Unmeßbarkleine.
Auf der Genauigkeit, mit welcher wir die Erscheinungen ins Unendlichkleine
verfolgen, beruht wesentlich die Erkenntnis ihres Kausalzusammenhangs.
Die Fortschritte der letzten Jahrhunderte in der
Erkenntnis der mechanischen Natur sind fast allein bedingt
durch die Genauigkeit der Konstruktion, welche durch
die Erfindung der Analysis des Unendlichen und die von
Archimed, Galilei und Newton aufgefundenen einfachen
Grundbegriffe, deren sich die heutige Physik bedient, möglich
geworden ist. In den Naturwissenschaft aber, wo die
einfachen Grundbegriffe zu solchen Konstruktionen bis jetzt
fehlen, verfolgt man, um den Kausalzusammenhang zu erkennen,
die Erscheinungen ins räumlich Kleine, soweit es
das Mikroskop nur getattet. Die Fragen über die
Maßverhältnisse des Raumes im Unmeßbarkleinen
gehören also nicht zu den müßigen.
Setzt man voraus, daß die Körper
unabhängig vom Ort existieren, so ist das Krümmungsmaß
überall konstant, und es folgt dann aus den astronomischen Messungen,
daß es nicht von Null verschieden sein kann; jedenfalls müßte
sein reziproker Wert eine Fläche sein, gegen welche das unsern
Teleskopen zugängliche Gebiet verschwinden müßte. Wenn
aber eine solche Unabhängigkeit der Körper vom Ort nicht
stattfindet, so kann man aus den Maßverhältnisse im
Großen nicht auf die im Unendlichkleinen schließen; es kann
dann in jedem Punkte das Krümmungsmaß in drei Richtungen
einen beliebigen Wert haben, wenn nur die ganze Krümmung
jedes Meßbaren Raumteils nicht merklich von Null
verschieden ist; noch komplizierte Verhältnisse können eintreten,
[pag. 20]
wenn die vorausgesetzte Darstellbarkeit eines Linienelements
durch die Quadratwurzel aus einem Differentialausdruck
zweiten Grades nicht stattfindet. Nun scheinen
aber die empirische Begriffe, in welchen die räumlichen
Maßbestimmungen gegründet sind, der Begriff des festen
Körpers und des Lichtstrahls, im Unendlichkleinen ihre
Gültigkeit zu verlieren; es ist also sehr wohl denkbar, daß
die Maßverhältnisse des Raumes im Unendlichkleinen den
Voraussetzungen der Geometrie nicht gemäß sind, und dies
würde die Erscheinungen auf einfachere Weise erklären
ließen.
Die Frage über die Gültigkeit der
Voraussetzungen der Geometrie im Unendlichkleinen hängt zusammen mit
der Frage nach dem innern Grunde der Maßverhältnisse des
Raumes. Bei dieser Frage, welche wohl noch zur Lehre vom
Raume gerechnet werden darf, kommt die obige Bemerkung
zur Anwendung, daß bei einer diskreten Mannigfaltigkeit
das Prinzip der Maßverhältnisse schon in dem Begriffe dieser
Mannigfaltigkeit enthalten ist, bei einer stetigen aber anders
woher hinzukommen muß. Es muß also entweder das dam
Raume zugrunde liegende Wirckliche eine diskrete Mannigfaltigkeit
bilden, oder den Grund der Maßverhältnisse
außerhalb, in darauf wirkenden bindenden Kräften gesucht
werden.
Die Entscheidung dieser Fragen kann nur gefunden
werden, indem man von der bisherigen durch die Erfahrung
bewährten Auffassung der Erscheinungen, wozu Newton den
Grund gelegt, ausgeht und diese durch Tatsachen, die sich
aus ihr nicht erklären lassen, getrieben allmählich umarbeitet;
solche Untersuchungen, welche, wie die hier geführte, von
allgemeinen Begriffen ausgehen, können nur dazu dienen,
daß diese Arbeit nicht durch die Beschränktheit der Begriffe
gehindert und der Fortschritt im Erkennen des Zusammenhangs
[pag. 21]
der Dinge nicht durch überlieferte Vorurteile gehemmt
wird.
Es führt dies hinüber in das Gebiet einer
andern Wissenschaft, in das Gebiet der Physik, welches wohl die Natur
der heutigen Veranlassung nicht zu betreten erlaubt.
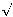
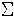 (dx)2); der Raum ist also unter diesem einfachsten
Falle enthalten. Der nächst einfache Fall würde wohl die
Mannigfaltigkeiten umfassen, in welchen sich das Linienelement durch die vierte
Wurzel aus einem Differentialausdrucke vierten Grades ausdrücken
läßt. Die Untersuchung dieser allgemeinern Gattung würde
zwar keine wesentlich andere Prinzipien erfordern, aber ziemlich zeitraubend sein
und verhältnismäßig auf die Lehre vom Raume wenig neues
Licht werfen, zumal da sich die Resultate nicht geometrisch ausdrücken
lassen; ich beschränke mich daher auf die Mannigfaltigkeiten, wo das
Linienelement durch die Quadratwurzel aus einem Differentialausdruck zweiten
Grades ausgedrückt wird. Man kann einen solchen Ausdruck in einen
andern ähnlichen transformieren, indem man für die n
unabhängigen Veränderlichen Funktionen von n neuen
unabhängigen Veränderlichen setzt. Auf diesem Wege wird man
aber nicht jeden Ausdruck in jeden transformieren können; denn der
Ausdruck enthält n(n + 1)/2 Koeffizienten, welche
willkürliche Funktionen der unabhängigen Veränderlichen sind;
durch Einführung neuer Veränderlichen wird man aber nur
n Relationen genügen und also nur n der
Koeffizienten gegebenen Größen gleich machen können. Es
sind dann die übrigen n(n - 1)/2
[pag. 10]
durch die Natur der darzustellenden Mannigfaltigkeit schon völlig
bestimmt, und zur Bestimmung ihrer Maßverhältnisse also
n(n - 1)/2 Funktionen des Orts erforderlich. Die
Mannigfaltigkeiten, in welchen sich, wie in der Ebene und im Raume, das
Linienelement auf die Form
(dx)2); der Raum ist also unter diesem einfachsten
Falle enthalten. Der nächst einfache Fall würde wohl die
Mannigfaltigkeiten umfassen, in welchen sich das Linienelement durch die vierte
Wurzel aus einem Differentialausdrucke vierten Grades ausdrücken
läßt. Die Untersuchung dieser allgemeinern Gattung würde
zwar keine wesentlich andere Prinzipien erfordern, aber ziemlich zeitraubend sein
und verhältnismäßig auf die Lehre vom Raume wenig neues
Licht werfen, zumal da sich die Resultate nicht geometrisch ausdrücken
lassen; ich beschränke mich daher auf die Mannigfaltigkeiten, wo das
Linienelement durch die Quadratwurzel aus einem Differentialausdruck zweiten
Grades ausgedrückt wird. Man kann einen solchen Ausdruck in einen
andern ähnlichen transformieren, indem man für die n
unabhängigen Veränderlichen Funktionen von n neuen
unabhängigen Veränderlichen setzt. Auf diesem Wege wird man
aber nicht jeden Ausdruck in jeden transformieren können; denn der
Ausdruck enthält n(n + 1)/2 Koeffizienten, welche
willkürliche Funktionen der unabhängigen Veränderlichen sind;
durch Einführung neuer Veränderlichen wird man aber nur
n Relationen genügen und also nur n der
Koeffizienten gegebenen Größen gleich machen können. Es
sind dann die übrigen n(n - 1)/2
[pag. 10]
durch die Natur der darzustellenden Mannigfaltigkeit schon völlig
bestimmt, und zur Bestimmung ihrer Maßverhältnisse also
n(n - 1)/2 Funktionen des Orts erforderlich. Die
Mannigfaltigkeiten, in welchen sich, wie in der Ebene und im Raume, das
Linienelement auf die Form 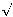
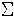 dx2
bringen läßt, bilden daher nur einen besonderen Fall der hier zu
untersuchenden Mannigfaltigkeiten; sie verdienen wohl einen besonderen
Namen, und ich will also diese Mannigfaltigkeiten, in welchen sich das Quadrat
des Linienelements auf die Summe der Quadrate von selbständigen
Differentialien bringen läßt, eben nennen. Um nun die wesentlichen
Verschiedenheiten sämlicher in der vorausgesetzten Form darstellbarer
Mannigfaltigkeiten übersehen zu können, ist es nötig, die von
der Darstellungsweise herrührenden zu beseitigen, was durch die Wahl der
verändelichen Größen nach einem bestimmten Prinzip erreicht
wird.
dx2
bringen läßt, bilden daher nur einen besonderen Fall der hier zu
untersuchenden Mannigfaltigkeiten; sie verdienen wohl einen besonderen
Namen, und ich will also diese Mannigfaltigkeiten, in welchen sich das Quadrat
des Linienelements auf die Summe der Quadrate von selbständigen
Differentialien bringen läßt, eben nennen. Um nun die wesentlichen
Verschiedenheiten sämlicher in der vorausgesetzten Form darstellbarer
Mannigfaltigkeiten übersehen zu können, ist es nötig, die von
der Darstellungsweise herrührenden zu beseitigen, was durch die Wahl der
verändelichen Größen nach einem bestimmten Prinzip erreicht
wird.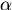 ein,
daß der Anfangswert des Quadrats des Linienelements gleich der Summe
der Quadrate dieser Ausdrücke wird, so daß die unabhängigen
Variabeln sind: die Größe s und die Verhältnisse der
Größen d
ein,
daß der Anfangswert des Quadrats des Linienelements gleich der Summe
der Quadrate dieser Ausdrücke wird, so daß die unabhängigen
Variabeln sind: die Größe s und die Verhältnisse der
Größen d