
E-mail:
gabriel.lord@ru.nl
GitHub
Google Scholar
Postal Address:
Department of Mathematics
Radboud University
Postbus 9010
6500 GL Nijmegen, NL.
My research interests are in the area of applied computational
mathematics and stochastics. I am interested in developing efficient numerical
techniques to simulate systems numerically, quantify uncertainty and in
proving convergence of these methods. I have worked on diverse
applications including reservoir simulation, volcanology, finance, neuroscience through to power grid cables for congestion management.
I would be happy to supervise PhD projects in many of the areas below.
Most preprints available on arXiv.
| OrcidID: 0000-0003-2152-1553 | Scopus Author ID: 7006574691 | Google Scholar | GitHub |
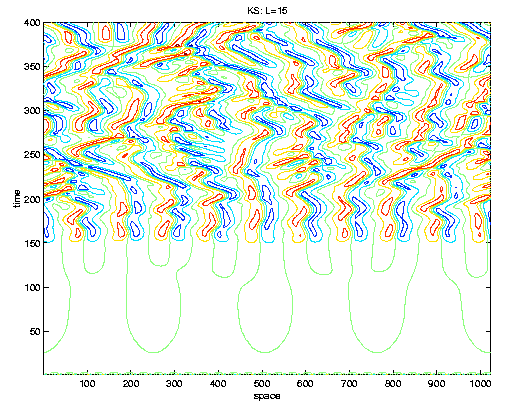
Stochastic (P)DEs

I am interested in developing new numerical methods for the numerical
simulation of stochastic DEs. I have worked
on SPDEs, as well as SDEs but am also interested in other
types of evolution equations.
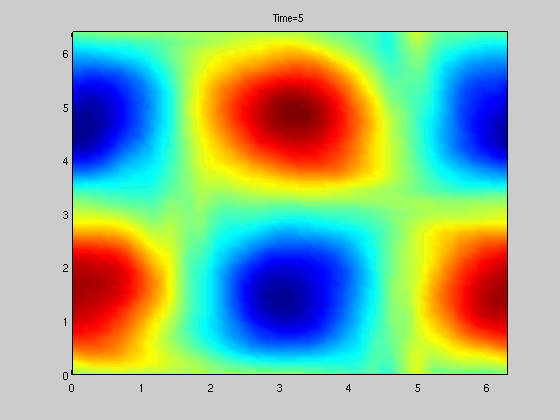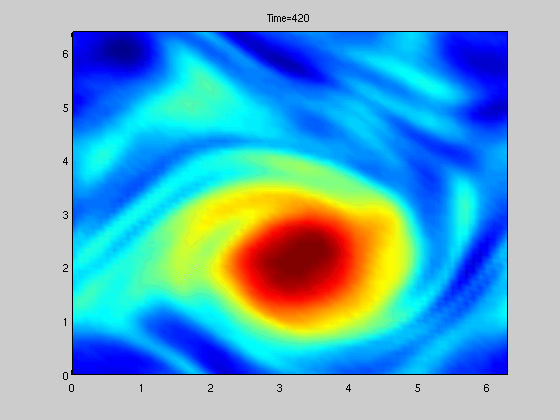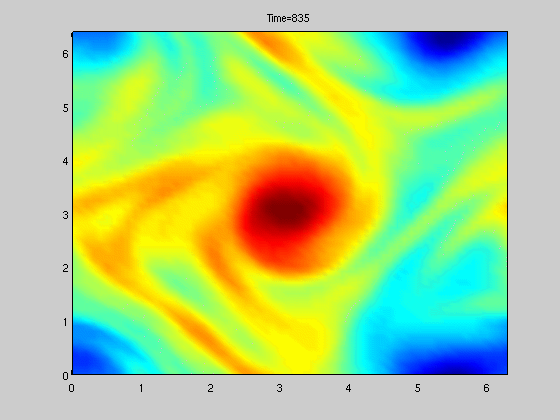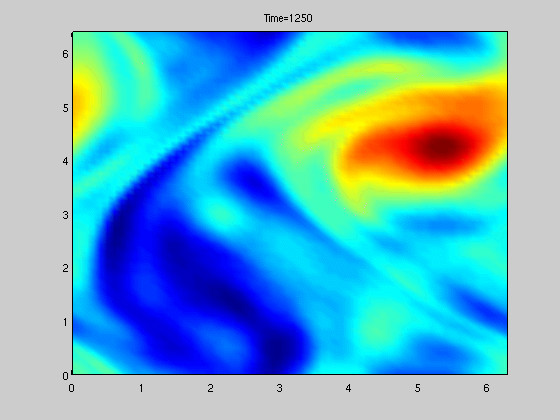
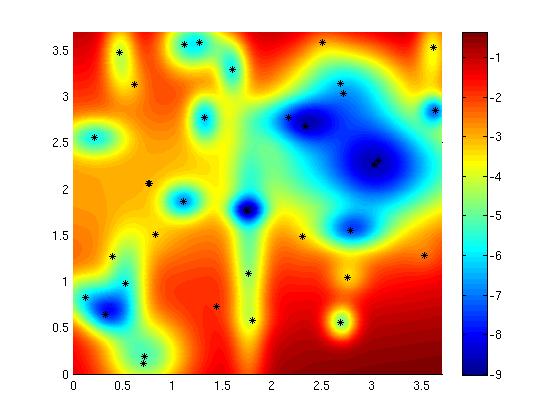
Figure to the right shows solution of a stochastically forced SPDE related to vorticity.
PhD Projects available
Figure to the right shows solution of a stochastically forced SPDE related to vorticity.
PhD Projects available
Mathematical Biology

I have had a long standing interest in computational
neuroscience and role of noise. Computational
models are being increasingly used to gain
insight into the behaviour and information processing abilities of
neurons. I am interested in models of single neurons, coupled neuron
dynamics as well as neural field models.
More recently I have been working with experimentalists looking at the
movement and interaction of vesicules and reaction with snap25 and syntaxin.
PhD Projects available
PhD Projects available
Computational Applied Analysis and Modelling

Applied problems from industry and other disciplines often lead to interesting mathematical and computational challenges. I am interested in quanitfying uncertainrty and parameter estimation in "real life" problems. This has led to work for example on volcano ash dispersal (with BGS) and heating of power cables with Alliander.
I am also interested in the interaction of numerical computations and
mathematical analysis and how good numerical approximations may give
insights.
PhD Projects available
PhD Projects available
Porous Media

Accurate and efficient simulation of flow in heterogeneous
porous media remains a challenging problem. The systems model potential ground
water contamination, underground reservoirs, subsurface storage.
In order to quantify the uncertainty in computations efficient methods
are required.
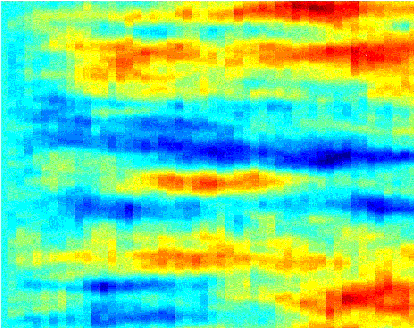
Figure shows solution of advection-reaction-diffusion equation through the SPE10 Model of a heterogeneous reservoir.
Figure shows solution of advection-reaction-diffusion equation through the SPE10 Model of a heterogeneous reservoir.
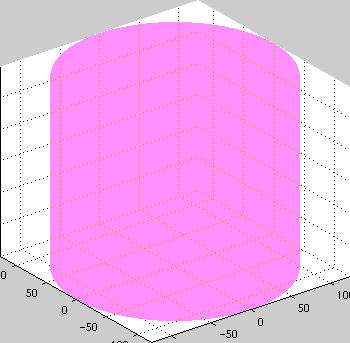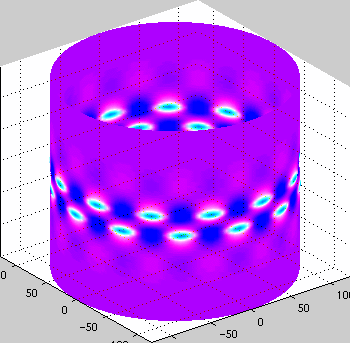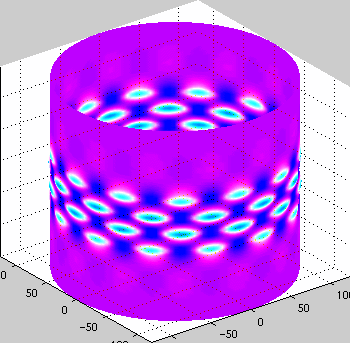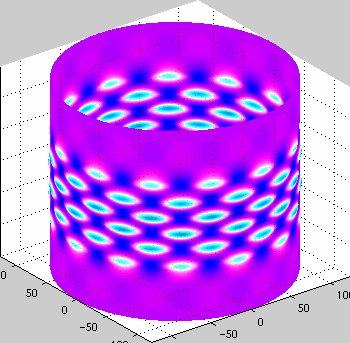
Cylinder Buckling

Work on buckling cylinders in primarily driven by the need for light
strong structures (such as silos, rockets, aircraft) and the desire to
understand how these structures fail. As anyone who has crushed a can
knows - cylinders are very strong but then buckle suddenly with a
great release of energy.
This work was onr of the first to look at snaking bifurcation
diagrams. We also characterized the mountain pass solutions.