Special cases which have been proved ::.
Here you will find subproblems of the conjecture which have already been proven or thought about.
Spanning Subgraphs of Random Graphs::.
Let G be a random grapph with n = 2d vertices in which each edge is taken randomly and independently with probability p = 1-ε, where ε is a positive small constant. Then G contains a copy of the d-cube for every fixed p > ½ and G does not contain a copy of the d-cube for p ≤ ¼.
It states the following theorem (and gives a sketch of the proof):
Theorem: Let G = G(n,p) be a random graph on a set V of n labelled vertices obtained by choosing each pair of vertices to be an edge randomly and independently, with probability p. Let H=(U,F) be a fixed simple graph on n vertices with maximum degree d, where (d2+1)2 < n. If
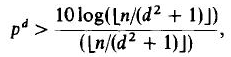
then the probability that G does not contain a copy of H is smaller than 1/n.
If we take H to be the d-cube: Qd, then for d large enough we have that (d2+1)2 < 2d (=n), so the right hand side of the equation can be shown to equal: 2-dO(d3). This means that (again, if d is large enough) for p>½: pd > 2-dO(d3). So for d large enough and p > ½ we have that G almost surely contains a copy of Qd.
If p ≤ ¼ G almost surely does not contain such a copy. This can be seen from remark 2 in the article: in case H is d-regular, the expected number of copies of H in G is at most n!pnd/2, which is o(1) for p = n -2/d (which equals ¼ if n=2d). This formula can be derived from the fact that there are at most n! possible d-cubes on n vertices, since for the first vertice there are n possible vertices to connect to, for the next there are at most (n-1) vertices to connect to and so on. The probability that every edge of a possible d-cube H is contained in G is p#edges of H = pnd/2. So the expected number of copies of H in G is n!pnd/2.
To understand the proof of this theorem, one other theorem in graph theory is needed and some theory on the existence of perfect matchings in graphs as well as the concept of taking the kth power of a graph and the definition of a simple graph:
Definition: a simple graph is an unweighted, undirected graph containing no graph loops or multiple edges.
(Definition from: WolframMathWorld)
Theorem of Hajnal and Szemerédi: Every graph with n vertices and maximum vertex degree Δ(G) ≤ k is (k+1)-colorable with all color classes of size ⌊n/(k+1)⌋ or ⌈n/(k+1)⌉.
(Theorem from: WolframMathWorld)
Definition: The kth power of a graph G is a graph with the same set of vertices as G and an edge between two vertices if there is a path of length at most k between them.
(Definition from: WolframMathWorld)
It is useful to realize that if G has maximum degree d then Gk has maximum degree dk. This is easily seen for k = 2: if a point p is a neighbour of maximal d other points, which all are a neighbour of maximal d points, then from p only d*d points can be reached in two steps. This argument can be extended by induction for k > 2 .
Definition: a matching M in a graph G is a set of pairwise non-adjacent edges.
A perfect matching M in a graph G is a matching which matches all vertices of a graph, that is: every vertex of the graph is incident to exactly one edge of the matching.
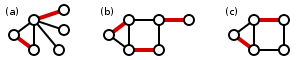
Matchings in graphs. Only (b) is a perfect matching.
(Definition and picture from: Wikipedia)
In the sketch of the proof of the theorem in the article the authors refer to some "known results on the existence of perfect matchings in graphs". I cannot find which "known results" they mean. They suggest to take a look at a book by Béla Bollobás: Random Graphs. A theorem which could be useful is the following:
Hall's theorem for graph theory: Let G:=(S+T,E) be a bipartite graph with two equally sized classes S and T. For a set X of vertices of G, let NG(X) denote the neighbourhood of X in G, i.e. the set of all vertices adjacent to some element of X.
A perfect matching exists in G if and only if for every subset X of S
(Theorem from: Wikipedia)
I will now give a summary of the proof of the theorem proposed by Alon and Füredi:
Let d be the maximum degree of H. Then the maximum degree of the square of H is d2. So by the theorem of Hajnal and Szemerédi the vertices of (the square of) H can be colored by d2 +1 colors. The number of points with the same color is either ⌊n/(d2+1)⌋ or ⌈n/(d2+1)⌉.
So a partition can be made of the set of vertices U of H in D:=d2+1 pairwise disjoint sets U1,...,UD with Uk an independent set in H, no two vertices of Uk have a common neighbour and #Uk is either ⌊n/(d2+1)⌋ or ⌈d2+1⌉.
Divide the set of vertices V of G in pairwise disjoint sets V1,...,VD, with |Vk|=|Uk| ∀ k.
It can now be shown that with high probability there is a one to one function f:U→V which maps Uk on Vk and H to a copy of H in G.
Define f on each Uk seperately. Start with an arbitrary mapping from U1 to V1. Use induction to define the rest of f: suppose f maps the induced subgraph of H in U1,...,Uk on a copy of it in V1,...,Vk. We can use the following construction to extend f and define it on Uk+1:
Let Uk+1 = {u1,...,um} and Vk+1={v1,...,vm}. Construct a bipartite graph B with classes of vertices X:={x1,...,xm} and Y := {y1,...,ym}. In this graph X can be seen to correspond to Uk+1 and Y to Vk+1. In B xi is connected to yj ⇔ f(ui) = vk, or said in a different way: {xi, yj} ∈ B ⇔ in G vj is adjacent to all vertices f(u) with {u,ui} ∈ U1,...,Uk.
Note that ∀ i,j the probability that this is so is ≤ pd, since vj maximally has to be connected to d vertices to be a part of the copy of H in G.
If a perfect matching exists in B, f can be defined by: f(ui) = vj if xi is matched to yj.
Apparently, it can be shown that the probability that no matching exists in Uk is 1/(nD). The chance that every Uk (with the exception of U1) contains a matching is (D-1)/(nD) ≤ D/(nD) = 1/n. I think this is under the condition that:
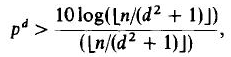(This could in some way be a consequence of Hall's theorem) Spanning Subgraphs of Random Graphs::.
In this article the following theorem is proved:
Theorem 1: Let p = p(d) = ¼ + 6log d/d. Then with probability tending to 1 as d → ∞ a random G ∈ G(2d,p) contains a copy of Qd.
This theorem is a direct result from another theorem stated and proved in the article. For this theorem, some notation is needed:
For a random variable X, X* is its standardization: (X-E(X))/σ(X)
N :=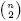 
The theorem works with the G(n,M) definition of random graphs.
Theorem 2: Suppose that M/N ≥ ¼ + 5log d/d, where n=2d, and let X = X(G) be the number of copies of Qd in G ∈ G(n,M). Then P[X=0] → 0 as d → ∞.
If in addition (1-M/N)log n → ∞, then X* converges in distribution to a standard normal distribution as d → ∞.
The first part of this theorem immediately implies theorem 1. Since as d → ∞ then G ∈ G(n,p) almost surely has more than M edges. Since p = M/N and ¼ + 6log d/d > ¼ + 5 log d/d theorem 1 can be concluded from theorem 2.
I will only look at the proof of the first part of the theorem 2. It uses another theorem. Some notation is needed to understand it:
n = |H| is the number of vertices of H
e(H) is the number of edges of H and can be written as αN (since the number of edges of h is a fraction of the total possible number of edges on n which is N).
Δ = Δ(H) is the maximum degree of H
eH(v) = max{e(F) : F ⊂ H, |F|=v}, the maximum number of edges of possible subgraphs of H with v vertices.
γ = γ(H) = max3≤v≤n{eH(v)/(v-2)} a modified maximum average degree of subgraphs of H.
Theorem 3: Let H(= H(i)) be a fixed sequence of graphs with n = |H| → ∞, and let γ = γ(H) be as above. Let e(H) = αN = α(n)N, and let p = p(n) ∈ (0,1) with pN an integer. Suppose that the following conditions hold:
and
Then, with probability tending to 1 as n → ∞, a random G ∈ G(n,pN) has a spanning subgraph isomorphic to H.
Theorem 2 can be proved from this by letting H = Qd, n = 2d and e(H) = αN, so α = d/(n-1). It suffices to verify the conditions of theorem 3 for p = ⌈(¼ + 5logd/d)N⌉/N.
The proof of theorem 3 is quite complicated. I will not describe it here, since it is described in detail in the article. The general idea of the proof is that Markov's inequality is used to bound P[X=0] in terms of E(X) and Var(X). In turn, Var(X) is bounded in terms of the extend to which the presence in G of one copy of H makes other copies more likely.