Behzad-Vizing Conjecture

Explanation

For a full understanding of the Behzad-Vizing conjecture, we will explain some definitions at this page. After that, we are going to talk about some variants of the conjecture.

There are different types of graph colourings. For example, for a graph G is:

• A vertex colouring an assignment of colours to the vertices of G such that adjacent vertices (i.e. vertices that are connected by an edge) receive different colours. The chromatic number denoted by χ(G) is the minimum number of colours needed for such a vertex colouring.


• An edge colouring an assignment of colours to the edges of G such that adjacent edges (i.e. edges that share a common vertex) receive different colours. The edge chromatic number χ'(G) is the minimum number of colours needed for such a edge colouring.


• A total colouring an assignment of colours to the vertices and edges of G such that:

  Adjacent vertices receive different colours.

  Adjacent edges receive different colours.

  Each edge receives another colour than it's endvertices.

  The total chromatic number χ"(G) is the minimum number of colours needed for such a total colouring.

In a simple graph loops and multiple edges are disallowed. In a multigraph they are not. The degree of a vertex v is the number of edges that have v as an endpoint. A loop increases the degree with two.

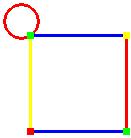
Sometimes the requirement of a graph being simple isn't added at Behzad-Vizing conjecture. A well-known site as open problem garden makes this mistake. To realise that this is a mistake, look at this graph G with Δ(G)=χ"(G)=4.

There are not only different names of the Behzad-Vizing conjecture abroad, the definitions of it are also not always the same. For example, there is a slight variant that has some space for multigraphs:

Note that the original conjecture (BVC) follows as a consequence of this variant (BVC'), since a simple graph has obviously the property that χ"(G)≥Δ(G)+1.

Hereafter, if we say "BVC is true for a graph G", we mean χ"(G)=Δ(G)+1 or χ"(G)=Δ(G)+2. With "BVC' is true for a graph H" we mean χ"(H)≤Δ(H)+2.