|
In his article Graph Theory, Jamie Morgenstern gives an incorrect proof of SSNC (pp. 2–4). Admittedly, I made the same mistake as he did when I was trying to solve SSNC. I thought that I had found a proof of SSNC, but I was not convinced of it, since it was quite an easy proof and I could not believe that no-one had come up with it before. However, I could not find an error in my reasoning either. Fortunately, a fellow student managed to discover the mistake.
Morgenstern's proof consists of three cases:
| Case 1: | Graphs with at least one vertex u of out-degree 0 |
| Because u has no neighbours, it cannot have any neighbours after squaring the graph either. |
| Case 2: | Graphs with all vertices of out-degree at least 1 |
| Let u be a vertex with exactly one out-going edge to, say, vertex v. Vertex v must also connect to another vertex, say, w. Then, after squaring the oriented graph, the edge (u,w) is added and the out-degree of vertex u is doubled. |
| Case 3: | Graphs with all vertices of out-degree at least 2 |
| Let u be a vertex with the minimum out-degree (at least 2). The vertices to which u is connected must reach "new" vertices, i.e. vertices other than u, otherwise there would be multiple edges between these vertices. Therefore, Morgenstern states that when the graph is squared, vertex u will have new arcs to these new vertices, and will have at least twice as many out-going edges as the original graph. |
The one thing Morgenstern fails to notice in his proof is that the vertices to which u is connected do not have to be connected to so-called "new" vertices; some of them may also be connected to each other. Therefore, Morgenstern's argument is invalid and his proof is incorrect. 
|
| In 2002, Vishal Gupta and Erin Haller published an article called A Proof of Seymour's Second Neighborhood Conjecture, in which they verify SSNC. As you will probably feel in your bones, the proof is incorrect.
The article contains a theorem, i.e. SSNC, and its proof makes use of two propositions and two lemmas:
| Proposition 1: | Suppose the oriented graph Γ has a vertex u of out-degree 0. Then Γ satisfies SSNC at u. |
| This is the same situation as Case 1 of Jamie Morgenstern's proof. |
| Proposition 2: | Suppose Γ is an oriented graph with some subgraph Γu containing a vertex u such that Γu satisfies SSNC at u and the out-degree of u in Γ is equal to the out-degree of u in Γu. Then Γ satisfies SSNC at u. |
| Because the out-degree of u is equal in both graphs, the number of vertices u points towards is equal in both graphs as well. Since SSNC holds in graph Γu, the number of neighbours of u at distance 2 in Γu is at least as high as the number of neighbours of u at distance 1 in Γu. If one combines this result with the fact that the number of neighbours of u at distance 2 in Γ is at least as high as the number of neighbours of u at distance 2 in Γu, then the proposition follows easily. |
| Lemma 1: | In every oriented tree Γ, there exists at least one vertex u such that the out-degree of u is 0. |
| Consider the leaves of a tree. If any of the leaves has a vertex with out-degree 0, then Lemma 1 is satisfied. Therefore, suppose that all leaves have out-degree 1. (Note that a leaf cannot have an out-degree of more than 1.) Remove all these leaves and the associated out-going edges; this creates a subtree. If any of the leaves of the subtree has out-degree 0, then these leaves also have out-degree 0 in the whole tree Γ, since all removed leaves and out-going edges only contribute to the in-degree of the leaves of the subtree. If all these new leaves have out-degree 0, the process may be repeated by removing leaves and the associated out-going edges from them. This process must terminate at some point, because the graph is finite. Therefore, there must be a leaf with out-degree 0, since all removed leaves and out-going edges only contribute to its in-degree. |
| Lemma 2: | Any oriented graph containing at least one oriented cycle satisfies SSNC for at least one vertex on that cycle. |
| First a definition is introduced which will help proving Lemma 2:
A j-complete sun Cjn of order j is a directed cycle of n vertices with j out-going edges, called rays, pointing outward from each vertex on the cycle.
Then it is proven that every j-complete sun satisfies SSNC at every vertex on the graph. To this end, note that every ray of a j-complete sun has out-degree 0, and thus, the sun satisfies SSNC at these vertices. It then suffices to consider only vertices on the cycle, which will be done by induction on j.
For j = 0, Cjn is a directed cycle without rays, which obviously satisfies SSNC at every point on the cycle. Assume Cj -1n satisfies SSNC at every point. Now consider a vertex vi on the cycle. This vertex has one more neighbour at distance 1 in Cjn than in Cj -1n, namely the vertex at the end of its additional ray. The vertex vi+1 on the cycle, towards which vi points, also has one additional neighbour at distance 1 on its ray, call it u. Since vi points towards vi+1 and vi+1 points towards u, u is at distance 2 from vi. Hence, vertex vi has at least as many neighbours at distance 1 as at distance 2. Since vi is arbitrary, this inequality holds for all vertices on the cycle.
Now Lemma 2 will be proven for any oriented graph Γ containing a directed cycle. Γ has a j-complete sun subgraph with j ≥ 0. Select such a subgraph for which j is the maximum possible. Because Cjn is maximal for some v0 on the cycle, the out-degree of both v0 in Γ and v0 in Cjn is equal to j+1. If this were not the case, and the out-degree of v0 in Γ would be greater than j+1 for all v on the cycle, there would exist a subgraph Ckn where k > j. By Proposition 2, Γ satisfies SSNC at vertex v0. |
| Theorem: | Every oriented graph Γ satisfies SSNC. |
| By Proposition 1 and Lemma 1, if Γ is a tree, Γ satisfies SSNC. By Lemma 2, if Γ contains a directed cycle, it satisfies SSNC. Therefore, it suffices to assume that Γ contains cycles, none of which is directed. This means that Γ contains at least one non-uniform cycle and no directed cycles.
Now choose a direction, either clockwise or anti-clockwise. (Without loss of generality, choose anti-clockwise.) Then consider a cycle in Γ. For this cycle, remove all directed edges oriented anti-clockwise and any now isolated vertices. Repeat this procedure until the resulting graph Γ0 has no cycles. This graph Γ0 must have at least one directed edge. Since Γ0 has no cycles, it is a forest. By Lemma 1, some vertex v0 of Γ0 has out-degree equal to 0. In their article, Gupta and Haller briefly prove that the addition of the erased directed edges will not alter the out-degree of this vertex v0. By Proposition 1, Γ satisfies SSNC at vertex v0. |
So, where is the mistake in Gupta and Vishal's proof? Granted, it is a very tricky one, as the proof seems to be fine. However, the induction step in the first half of the proof of Lemma 2 is incorrect. In this part of the proof, a vertex vi on the cycle is considered and it is said that this vertex has one more neighbour at distance 1 in Cjn than in Cj+1n, namely the vertex at the end of its additional ray. Next, the vertex vi+1 on the cycle, which vi points towards, is considered and this vertex also has one additional neighbour at distance 1 on its ray, say u. Therefore, Gupta and Haller conclude, u is at distance 2 from vi. But this does not have to be true! The vertex u can be the same vertex as the vertex at the end of the additional ray of vertex vi!
What goes wrong in the first place is the definition of a j-complete sun Cjn. The definition does not mention that the vertices at the end of a ray have to be different vertices. If you do not restate the definition, it is not true that every oriented graph with a directed cycle contains a sun, and if you change the definition, it is not true that every vertex of the cycle of a sun satisfies SSNC. Hence, the proof of Lemma 2, and therefore the proof of SSNC, is incomplete and, in particular, incorrect. 
Here is an example of why the definition of a j-complete sun Cjn is shady. On the left you see a 2-complete sun C25 in the way Gupta and Haller intended it to be; on the right you see the same 2-complete sun, which should be correct according to the definition, but which is not examined in the proof:
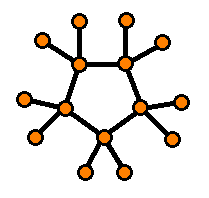 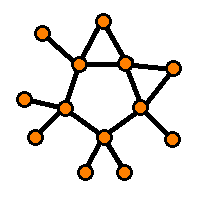
|



