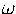 , doch allen bestaande
[pag. 143]
uit gelijke elementen
14), zoodat we ons b.v. de
willekeurige oneindige duaalbreuken nooit af, dus
nooit geïndividualiseerd kunnen denken, omdat het
aftelbaar oneindig aantal cijfers achter de komma niet
is te zien als een aftelbaar aantal gelijke dingen),
en tenslotte het intuitief continuum, (met behulp
waarvan we vervolgens het gewone continuum, het
meetbaar continuum, hebben geconstrueerd).
, doch allen bestaande
[pag. 143]
uit gelijke elementen
14), zoodat we ons b.v. de
willekeurige oneindige duaalbreuken nooit af, dus
nooit geïndividualiseerd kunnen denken, omdat het
aftelbaar oneindig aantal cijfers achter de komma niet
is te zien als een aftelbaar aantal gelijke dingen),
en tenslotte het intuitief continuum, (met behulp
waarvan we vervolgens het gewone continuum, het
meetbaar continuum, hebben geconstrueerd).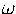 van de rij der eindige ordetypen: 0, 1, 2, . . .
Er is dan ook niets tegen, om
van de rij der eindige ordetypen: 0, 1, 2, . . .
Er is dan ook niets tegen, om
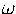 te stellen als een
nieuw ordegetal, en weer op nieuw te gaan tellen
te stellen als een
nieuw ordegetal, en weer op nieuw te gaan tellen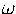 ,
,
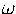 + 1,
+ 1,
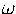 + 2, . . .
2
+ 2, . . .
2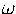 ,
2
,
2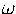 + 1, . . .
m
+ 1, . . .
m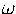 + n, . . .
+ n, . . .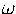 2; we openen
ons zoo weer een grooter gebied van volgend een
[pag. 145]
welgeordende rij op elkaar volgende ordegetallen,
waarvan de uitdrukking geschiedt door den algemeenen
vorm:
2; we openen
ons zoo weer een grooter gebied van volgend een
[pag. 145]
welgeordende rij op elkaar volgende ordegetallen,
waarvan de uitdrukking geschiedt door den algemeenen
vorm: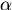 :
: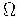 invoert, en dat noemt:
eerste ordegetal der derde getalklasse. Maar
invoert, en dat noemt:
eerste ordegetal der derde getalklasse. Maar
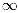 b'',
gelezen: a aequivalent met b), om
uit te drukken dat a en b een-eenduidig op elkaar
afbeeldbaar zijn):
b'',
gelezen: a aequivalent met b), om
uit te drukken dat a en b een-eenduidig op elkaar
afbeeldbaar zijn):
 x
voor alle dingen, waarvoor de
[pag. 161]
bewering
x
voor alle dingen, waarvoor de
[pag. 161]
bewering
 wordt
ingevoerd zóó, dat
k
wordt
ingevoerd zóó, dat
k