

| Seite | ||
| Vorwort | 1 | |
| §. 1. | Eigenschaften der rationalen Zahlen | 5 |
| §. 2. | Vergleichung der rationalen Zahlen mit den Puncten einer geraden Linie | 7 |
| §. 3. | Stetigkeit der geraden Linie | 9 |
| §. 4. | Schöpfung der irrationalen Zahlen | 12 |
| §. 5. | Stetigkeit des Gebietes der irrationalen Zahlen | 17 |
| §. 6. | Rechnungen mit reellen Zahlen | 19 |
| §. 7. | Infinitesimal-Analysis | 22 |
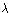 von der Art, daß
von der Art, daß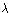 2 < D
< (
2 < D
< (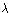 + 1)2
+ 1)2
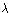 u < t <
(
u < t <
(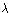 + 1)u
+ 1)u
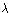 u
u
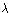 t,
t,
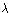 2 -
D)(t2 - Du2)
= 0,
2 -
D)(t2 - Du2)
= 0,
 , welche wir als durch diesen
Schnitt (A1, A2)
vollständig definirt ansehen; wir werden sagen, daß die Zahl
, welche wir als durch diesen
Schnitt (A1, A2)
vollständig definirt ansehen; wir werden sagen, daß die Zahl
 diesem Schnitt entspricht, oder
daß sie diesen Schnitt hervorbringt. Es entspricht also von jeßt ab
jedem bestimmten Schnitt eine bestimmte rationale oder irrationale Zahl und wir
sehen zwei Zahlen stets und nur dann
[pag. 15]
als verschieden oder ungleich an, wenn sie wesentlich
verschiedenen Schnitten entsprecheb.
diesem Schnitt entspricht, oder
daß sie diesen Schnitt hervorbringt. Es entspricht also von jeßt ab
jedem bestimmten Schnitt eine bestimmte rationale oder irrationale Zahl und wir
sehen zwei Zahlen stets und nur dann
[pag. 15]
als verschieden oder ungleich an, wenn sie wesentlich
verschiedenen Schnitten entsprecheb. und ß hervorgebracht werden. Offenbar ist ein Schnitt
(A1, A2) schon
vollständig gegeven, wenn eine der beiden Classen, z.B. die erste
A1, bekannt is, weil die zweite
A2 aus allen nicht in
A1 enthalteten rationalen Zahlen besteht, und die
charakteristische Eigenschaft einer solchen ersten Classe
A1 liegt darin, daß sie, wenn die Zahl
a1 in ihr enthalten ist, auch alle kleineren Zahlen als
a1 enthät. Vergleicht man nun zwei solche
erste Classen A1, B1
mit einander, so kann es 1) sein, daß sie vollständig identisch sind,
d.h., daß jede in A1 enthaltene Zahl
a1 auch in B1 , und
daß jede in B1 enthaltene Zahl
b1 auch in A1
enthalten ist. In diesem Falle ist dann nothwendig auch
A2 identisch mit B2,
die beiden Schnitte sind vollständig identisch, was wir in Zeichnen durch
und ß hervorgebracht werden. Offenbar ist ein Schnitt
(A1, A2) schon
vollständig gegeven, wenn eine der beiden Classen, z.B. die erste
A1, bekannt is, weil die zweite
A2 aus allen nicht in
A1 enthalteten rationalen Zahlen besteht, und die
charakteristische Eigenschaft einer solchen ersten Classe
A1 liegt darin, daß sie, wenn die Zahl
a1 in ihr enthalten ist, auch alle kleineren Zahlen als
a1 enthät. Vergleicht man nun zwei solche
erste Classen A1, B1
mit einander, so kann es 1) sein, daß sie vollständig identisch sind,
d.h., daß jede in A1 enthaltene Zahl
a1 auch in B1 , und
daß jede in B1 enthaltene Zahl
b1 auch in A1
enthalten ist. In diesem Falle ist dann nothwendig auch
A2 identisch mit B2,
die beiden Schnitte sind vollständig identisch, was wir in Zeichnen durch
 = ß oder ß =
= ß oder ß =
 andeuten.
andeuten. = a'1
= b'2 hervorgebracht. Von dem anderen Schnitte
(B1, B2) wissen wir
schon, daß alle Zahlen b1 in
B1 auch in A1
enthalten und kleiner als die Zahl a'1 =
b'2 sind, welche in B2
enthalten ist; jede andere in B2 enthaltene
[pag. 16]
Zahl b2 muß aber größer als
b'2 sein, weil sie sonst auch kleiner als
a'1, also in A1 und
folglich auch in B1 enthalten wäre; mithin ist
b'2 die kleinste unter allen in
B2 enthaltenen Zahlen, und folglich wird auch der
Schnitt (B1, B2) durch
dieselbe rationale Zahl ß = b'2 =
a'1 =
= a'1
= b'2 hervorgebracht. Von dem anderen Schnitte
(B1, B2) wissen wir
schon, daß alle Zahlen b1 in
B1 auch in A1
enthalten und kleiner als die Zahl a'1 =
b'2 sind, welche in B2
enthalten ist; jede andere in B2 enthaltene
[pag. 16]
Zahl b2 muß aber größer als
b'2 sein, weil sie sonst auch kleiner als
a'1, also in A1 und
folglich auch in B1 enthalten wäre; mithin ist
b'2 die kleinste unter allen in
B2 enthaltenen Zahlen, und folglich wird auch der
Schnitt (B1, B2) durch
dieselbe rationale Zahl ß = b'2 =
a'1 =  hervorgebracht. Die beiden Schnitte sind daher nur unwesentlich
verschieden.
hervorgebracht. Die beiden Schnitte sind daher nur unwesentlich
verschieden. und ß ebenfalls
verschieden von einander, und zwar sagen wir, daß
und ß ebenfalls
verschieden von einander, und zwar sagen wir, daß
 größer als
ß, daß ß kleiner als
größer als
ß, daß ß kleiner als
 ist, was wir in Zeichen sowohl
durch
ist, was wir in Zeichen sowohl
durch  > ß, als durch
ß <
> ß, als durch
ß <  ausdrücken.
Hierbei ist hervorzuheben, daß diese Definition vollständig mit der
früheren zusammenfällt, wenn beide Zahlen
ausdrücken.
Hierbei ist hervorzuheben, daß diese Definition vollständig mit der
früheren zusammenfällt, wenn beide Zahlen
 , ß rational sind.
, ß rational sind. = a'2
= b'1 = ß hervorgebracht. Giebt es aber 5)
in B1 mindestens zwei verschiedene Zahlen, welche
nicht in A1 enthalten sind, so ist ß >
= a'2
= b'1 = ß hervorgebracht. Giebt es aber 5)
in B1 mindestens zwei verschiedene Zahlen, welche
nicht in A1 enthalten sind, so ist ß >
 ,
,
 < ß.
< ß. , ß; aber diese Wahl ist erst
jeßt nachträglich gerechtfertigt. Gerade bei solchen Untersuchungen
hat man sich auf das Sorgfältige zu hüten, daß man selbst bei
dem besten Willen,
[pag. 17]
ehrlich zu zein, durch eine voreilige Wahl von Ausdrücken, welche anderen
schon entwickelten Vorstellungen entlehnt sind, sich nicht verleiten lasse,
unerlaubte Uebertragungen aus dem einen Gebiete in das andere
vorzunehmen.
, ß; aber diese Wahl ist erst
jeßt nachträglich gerechtfertigt. Gerade bei solchen Untersuchungen
hat man sich auf das Sorgfältige zu hüten, daß man selbst bei
dem besten Willen,
[pag. 17]
ehrlich zu zein, durch eine voreilige Wahl von Ausdrücken, welche anderen
schon entwickelten Vorstellungen entlehnt sind, sich nicht verleiten lasse,
unerlaubte Uebertragungen aus dem einen Gebiete in das andere
vorzunehmen. > ß, so ergiebt sich,
daß die kleinere Zahl ß, wenn sie rational ist, gewiß der
Classe A1 angehöhrt; da es nämlich in
A1 eine Zahl a'1 =
b'2 giebt, welche der Classe
B2 angehöht, so ist die Zahl ß, mag sie
die größte Zahl in B1 oder die kleinste
Zahl B2 sein, gewiß <
a'1 und folglich in A1
enthalten. Ebenso ergiebt sich aus
> ß, so ergiebt sich,
daß die kleinere Zahl ß, wenn sie rational ist, gewiß der
Classe A1 angehöhrt; da es nämlich in
A1 eine Zahl a'1 =
b'2 giebt, welche der Classe
B2 angehöht, so ist die Zahl ß, mag sie
die größte Zahl in B1 oder die kleinste
Zahl B2 sein, gewiß <
a'1 und folglich in A1
enthalten. Ebenso ergiebt sich aus
 > ß, daß die
größere Zahl
> ß, daß die
größere Zahl  , wenn sie
rational ist, gewiß der Classe B2
angehouml;rt, weil
, wenn sie
rational ist, gewiß der Classe B2
angehouml;rt, weil  >
a'1 ist. Vereinigt man beide Betrachtungen, so
erhält man folgendes Resultat: Wird ein Schnitt
(A1, A2) durch die Zahl
>
a'1 ist. Vereinigt man beide Betrachtungen, so
erhält man folgendes Resultat: Wird ein Schnitt
(A1, A2) durch die Zahl
 hervorgebracht, so gehört
irgend eine rationale Zahl zu der Classe A1, oder zu
der Classe A2, je nachdem sie kleiner oder
größer ist als
hervorgebracht, so gehört
irgend eine rationale Zahl zu der Classe A1, oder zu
der Classe A2, je nachdem sie kleiner oder
größer ist als  ; ist die
Zahl
; ist die
Zahl  selbst rational, so kann sie der
einen oder der anderen Classe angehören.
selbst rational, so kann sie der
einen oder der anderen Classe angehören. > ß, giebt es also unendlich
viele Zahlen in A1, welche nicht in
B1 enthalten sind, so giebt es auch unendlich viele
solche Zahlen, welche zugleich von
> ß, giebt es also unendlich
viele Zahlen in A1, welche nicht in
B1 enthalten sind, so giebt es auch unendlich viele
solche Zahlen, welche zugleich von  und von ß verschieden sind; jede solche rationale Zahl c ist <
und von ß verschieden sind; jede solche rationale Zahl c ist <
 , weil sie in
A1 enthalten ist, und sie ist zugleich > ß,
weil sie in B2 enthalten ist.
, weil sie in
A1 enthalten ist, und sie ist zugleich > ß,
weil sie in B2 enthalten ist. >
ß, und ß >
>
ß, und ß >  , so ist
auch
, so ist
auch  >
>  . Wir wollen sagen, daß die Zahl
ß zwischen den Zahlen
. Wir wollen sagen, daß die Zahl
ß zwischen den Zahlen  ,
,
 liegt.
[pag. 18]
liegt.
[pag. 18] ,
,
 zwei verschiedene Zahlen, so
giebt es immer unendlich viele verschiedene Zahlen ß, welche zwischen
zwei verschiedene Zahlen, so
giebt es immer unendlich viele verschiedene Zahlen ß, welche zwischen
 ,
,
 liegen.
liegen. eine
bestimmte Zahl, so zerfallen alle Zahlen des Systems R in zwei Classen
A1 und A2, deren jede unendlich viele
Individuen enthält; die erste Classe A1 umfaßt
alle die Zahlen
eine
bestimmte Zahl, so zerfallen alle Zahlen des Systems R in zwei Classen
A1 und A2, deren jede unendlich viele
Individuen enthält; die erste Classe A1 umfaßt
alle die Zahlen
 1 welche <
1 welche <
 sind, die zweite Classe
A2 umfaßt alle die Zahlen
sind, die zweite Classe
A2 umfaßt alle die Zahlen
 2, welche >
2, welche >
 sind; die Zahl
sind; die Zahl
 selbst kann nach Belieben der
ersten oder der zweiten Classe zugetheilt werden, und sie ist dann entsprechend
die größte Zahl der ersten oder die kleinste Zahl der zweiten Classe.
In jedem Falle ist die Zerlegung des Systems R in die beiden Classen
A1, A2 von der Art, daß jede Zahl der
ersten Classe A1 kleiner als jede Zahl der zweiten Classe
A2 ist, und wir sagen, daß diese Zerlegung durch die
Zahl
selbst kann nach Belieben der
ersten oder der zweiten Classe zugetheilt werden, und sie ist dann entsprechend
die größte Zahl der ersten oder die kleinste Zahl der zweiten Classe.
In jedem Falle ist die Zerlegung des Systems R in die beiden Classen
A1, A2 von der Art, daß jede Zahl der
ersten Classe A1 kleiner als jede Zahl der zweiten Classe
A2 ist, und wir sagen, daß diese Zerlegung durch die
Zahl  hervorgebracht wird.
hervorgebracht wird. 1 der
Classe A1 kleiner ist als jede Zahl
1 der
Classe A1 kleiner ist als jede Zahl
 2 der Classe
A2, so existirt eine und nur eine Zahl
2 der Classe
A2, so existirt eine und nur eine Zahl
 , durch welche diese Zerlegung
hervorgebracht wird.
, durch welche diese Zerlegung
hervorgebracht wird. die völlig bestimmte Zahl,
welche diesen Schnitt (A1,
A2) hervorbringt. Ist nun ß irgend eine von
die völlig bestimmte Zahl,
welche diesen Schnitt (A1,
A2) hervorbringt. Ist nun ß irgend eine von
 verschiedenen Zahl, so giebt es
immer unendlich viele rationale Zahlen c, welche zwischen
verschiedenen Zahl, so giebt es
immer unendlich viele rationale Zahlen c, welche zwischen
 und ß liegen. Ist ß <
und ß liegen. Ist ß <
 , so ist c <
, so ist c <
 ; mithin gehört c
der [pag. 19]
Classe A1 und folglich auch der Classe
A1 an, und da zugleich ß < c ist, so
gehört auch ß derselben Classe A1 an, weil jede
Zahl in A2 größer ist als jede Zahl c in
A1. Ist aber ß >
; mithin gehört c
der [pag. 19]
Classe A1 und folglich auch der Classe
A1 an, und da zugleich ß < c ist, so
gehört auch ß derselben Classe A1 an, weil jede
Zahl in A2 größer ist als jede Zahl c in
A1. Ist aber ß >
 , so ist c >
, so ist c >
 ; mithin gehört c
der Classe A2 und folglich auch der Classe
A2 an, und da zugleich ß > c ist, so
gehört auch ß derselben Classe A2 an, weil jede
Zahl in A1 kleiner ist als jede Zahl c in
A2. Mithin gehört jede von
; mithin gehört c
der Classe A2 und folglich auch der Classe
A2 an, und da zugleich ß > c ist, so
gehört auch ß derselben Classe A2 an, weil jede
Zahl in A1 kleiner ist als jede Zahl c in
A2. Mithin gehört jede von
 verschiedene Zahl ß der
Classe A1 oder der Classe A2 an, je
nachdem ß <
verschiedene Zahl ß der
Classe A1 oder der Classe A2 an, je
nachdem ß <  oder ß
>
oder ß
>  ist; folglich ist
ist; folglich ist
 selbst entweder die
größte Zahl in A2, d.h.
selbst entweder die
größte Zahl in A2, d.h.
 ist eine und offenbar die einzige
Zahl, durch welche die Zerlegung von R in die Classen A1,
A2 hervorgebracht wird, was zu beweisen war.
ist eine und offenbar die einzige
Zahl, durch welche die Zerlegung von R in die Classen A1,
A2 hervorgebracht wird, was zu beweisen war. , ß auf die Rechnungen mit
rationalen Zahlen zurückzuführen, kommt es nur darauf an, aus den
Schnitten (A1, A2) und
(B1, B2), welche durch
die Zahlen
, ß auf die Rechnungen mit
rationalen Zahlen zurückzuführen, kommt es nur darauf an, aus den
Schnitten (A1, A2) und
(B1, B2), welche durch
die Zahlen  und ß im Systeme
R hervorgebracht werden, den Schnitt
(C1, C2) zu definiren,
welcher dem Rechnungsresultate
und ß im Systeme
R hervorgebracht werden, den Schnitt
(C1, C2) zu definiren,
welcher dem Rechnungsresultate  entsprechen soll. Ich beschränke mich hier auf die Durchführung des
einfachsten Beispieles, der Addition.
entsprechen soll. Ich beschränke mich hier auf die Durchführung des
einfachsten Beispieles, der Addition. , ß
rational, so ist jede in C1 enthaltene Zahl
c1 <
, ß
rational, so ist jede in C1 enthaltene Zahl
c1 <
 + ß, weil
a1 <
+ ß, weil
a1 <
 , b1
< ß, also auch a1 +
b1 <
, b1
< ß, also auch a1 +
b1 <
 + ß ist; wäre
[pag. 20]
ferner eine in C2 enthaltene Zahl
c2 <
+ ß ist; wäre
[pag. 20]
ferner eine in C2 enthaltene Zahl
c2 <  + ß, also
+ ß, also  + ß =
c2 + p, wo p eine positive
rationale Zahl bedeutet, so wäre
+ ß =
c2 + p, wo p eine positive
rationale Zahl bedeutet, so wäre - ½p) +
(ß - ½p),
- ½p) +
(ß - ½p),
 - ½p
eine Zahl in A1, und ß - ½p
eine Zahl in B1 ist; folglich ist jede in
C2 enthaltene Zahl c2
>
- ½p
eine Zahl in A1, und ß - ½p
eine Zahl in B1 ist; folglich ist jede in
C2 enthaltene Zahl c2
>  + ß. Mithin
wird in diesem Falle der Schnitt (C1,
C2) durch die Summe
+ ß. Mithin
wird in diesem Falle der Schnitt (C1,
C2) durch die Summe
 + ß hervorgebracht. Man
verstößt daher nicht gegen die in der Arithmetik der rationalen
Zahlen geltende Definition, wenn man in allen Fällen unter der
Summe
+ ß hervorgebracht. Man
verstößt daher nicht gegen die in der Arithmetik der rationalen
Zahlen geltende Definition, wenn man in allen Fällen unter der
Summe  + ß von
zwei beliebigen reellen Zahlen
+ ß von
zwei beliebigen reellen Zahlen  ,
ß diejenige Zahl
,
ß diejenige Zahl  versteht,
durch welche der Schnitt (C1,
C2) hervorgebracht wird. Ist ferner nur eine der
beiden Zahlen
versteht,
durch welche der Schnitt (C1,
C2) hervorgebracht wird. Ist ferner nur eine der
beiden Zahlen  , ß, z.B.
, ß, z.B.
 , rational, so überzeugt man
sich leicht, daß es keinen Einfluß auf die Summe
, rational, so überzeugt man
sich leicht, daß es keinen Einfluß auf die Summe
 =
=
 + ß hat, ob man die Zahl
+ ß hat, ob man die Zahl
 in die Classe
A1 oder in die Classe
A2 aufnimmt.
in die Classe
A1 oder in die Classe
A2 aufnimmt.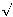 2.
2.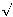 3 =
3 =
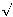 6), welche meines Wissens bisher
nie bewiesen sind. Die Weitläufigkeiten, welche bei den Definitionen der
complicirteren Operationen zu befürchten sind, liegen theils in der Natur
der Sachem zum größten Theil aber, lassen sie sich vermeiden. Sehr
nüßlich ist in dieser Beziehung der Begriff eines
Intervalls, d.h. eines Systems A von rationalen Zahlen,
welches folgende charakteristische Eigenschaft besißt: sind a
und a' Zahlen des Systems A, so sind auch alle zwischen
a und a' liegenden rationalen Zahlen in A
enthalten. Das System R aller rationalen Zahlen, ebenso die beiden
Classen eines jeden Schnittes sind Intervalle. Giebt es aber eine rationale Zahl
a1, welche kleiner, und eine rationale Zahl
a2, welche größer ist, als jede Zahl des
Intervalls A, so heiße A ein endliches
[pag. 21]
Intervall; es giebt dann offenbar unendlich viele Zahlen von derselben
Beschaffenheit wie a1, und unendlich viele Zahlen
von derselben Beschaffenheit wie a2; daß
ganze gebiet R zerfällt in drei Stücke,
A1, A, A2, und es treten zwei
vollständig bestimmte rationale Zahlen
6), welche meines Wissens bisher
nie bewiesen sind. Die Weitläufigkeiten, welche bei den Definitionen der
complicirteren Operationen zu befürchten sind, liegen theils in der Natur
der Sachem zum größten Theil aber, lassen sie sich vermeiden. Sehr
nüßlich ist in dieser Beziehung der Begriff eines
Intervalls, d.h. eines Systems A von rationalen Zahlen,
welches folgende charakteristische Eigenschaft besißt: sind a
und a' Zahlen des Systems A, so sind auch alle zwischen
a und a' liegenden rationalen Zahlen in A
enthalten. Das System R aller rationalen Zahlen, ebenso die beiden
Classen eines jeden Schnittes sind Intervalle. Giebt es aber eine rationale Zahl
a1, welche kleiner, und eine rationale Zahl
a2, welche größer ist, als jede Zahl des
Intervalls A, so heiße A ein endliches
[pag. 21]
Intervall; es giebt dann offenbar unendlich viele Zahlen von derselben
Beschaffenheit wie a1, und unendlich viele Zahlen
von derselben Beschaffenheit wie a2; daß
ganze gebiet R zerfällt in drei Stücke,
A1, A, A2, und es treten zwei
vollständig bestimmte rationale Zahlen
 1,
1,
 2 auf, welche
resp. die untere und obere (oder die kleinere und größere)
Grenze des Intervalls A genannt werden können; die
untere Grenze
2 auf, welche
resp. die untere und obere (oder die kleinere und größere)
Grenze des Intervalls A genannt werden können; die
untere Grenze  1
ist durch den Schnitt bestimmt, bei welchem die erste Classe durch das System
A1 gebildet wird, und die obere Grenze
1
ist durch den Schnitt bestimmt, bei welchem die erste Classe durch das System
A1 gebildet wird, und die obere Grenze
 2 durch den
Schnitt, bei welchem A2 die zweite Classe bildet.
Von jeder rationalen oder irrationalen Zahl
2 durch den
Schnitt, bei welchem A2 die zweite Classe bildet.
Von jeder rationalen oder irrationalen Zahl
 , welche zwischen
, welche zwischen
 1 und
1 und
 2 liegt, mag
gesagt werden, sie liege innerhalb des Intervalls A. Sind
alle Zahlen eines Intervalls A auch Zahlen eines Intervalls B,
so heiße A ein Stück von B.
2 liegt, mag
gesagt werden, sie liege innerhalb des Intervalls A. Sind
alle Zahlen eines Intervalls A auch Zahlen eines Intervalls B,
so heiße A ein Stück von B.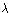 das Resultat einer mit den Zahlen
das Resultat einer mit den Zahlen
 , ß,
, ß,
 ... angestellten Rechnung, und
liegt
... angestellten Rechnung, und
liegt 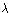 innerhalb des Intervalls
L, so lassen sich Intervalle A, B, C ... angeben, innerhalb
deren die Zahlen
innerhalb des Intervalls
L, so lassen sich Intervalle A, B, C ... angeben, innerhalb
deren die Zahlen  , ß,
, ß,
 ... liegen, und von der Art,
daß das Resultat derselben Rechnung, in welcher die Zahlen
... liegen, und von der Art,
daß das Resultat derselben Rechnung, in welcher die Zahlen
 , ß,
, ß,
 ... durch beliebige Zahlen der
Intervalle A, B, C... erfeßt werden, jedesmal eine innerhalb des
Intervalls L liegende Zahl wird.'' Die abschreckende
Schwerfälligkeit aber, welche dem Ausspruche eines solchen Saßes
anklebt, überseugt uns, daß hier etwas geschehen muß, um
der Sprache zu Hülfe zu kommen; dies wird in der That auf die
vollkommenste Weise erreicht, wenn man die Begriffe
[pag. 22]
der veränderlichen Größen, der
Functionen, der Grenzwehrte einführt, und zwar
wird es das Zweckmäßigste sein, schon die Definitionen der
einfachsten arithmetischen Operationen auf diese Begriffe zu gründen,
was hier jedoch nicht weiter ausgeführt werden kann.
... durch beliebige Zahlen der
Intervalle A, B, C... erfeßt werden, jedesmal eine innerhalb des
Intervalls L liegende Zahl wird.'' Die abschreckende
Schwerfälligkeit aber, welche dem Ausspruche eines solchen Saßes
anklebt, überseugt uns, daß hier etwas geschehen muß, um
der Sprache zu Hülfe zu kommen; dies wird in der That auf die
vollkommenste Weise erreicht, wenn man die Begriffe
[pag. 22]
der veränderlichen Größen, der
Functionen, der Grenzwehrte einführt, und zwar
wird es das Zweckmäßigste sein, schon die Definitionen der
einfachsten arithmetischen Operationen auf diese Begriffe zu gründen,
was hier jedoch nicht weiter ausgeführt werden kann. nähert, wenn x im
Laufe des Processes definitiv zwischen je zwei Zahlen zu liegen kommt,
zwischen denen
nähert, wenn x im
Laufe des Processes definitiv zwischen je zwei Zahlen zu liegen kommt,
zwischen denen  selbst liegt, oder
was dasselbe ist, wenn die Differenz x -
selbst liegt, oder
was dasselbe ist, wenn die Differenz x -
 absolut genommen unter jeden
gegebenen, von Null verschiedenen Werth definitiv herabsinkt.
absolut genommen unter jeden
gegebenen, von Null verschiedenen Werth definitiv herabsinkt. 2 von der Art,
daß stets x <
2 von der Art,
daß stets x <
 2 bleibt; ich
bezeichne mit A2 das System aller dieser Zahlen
2 bleibt; ich
bezeichne mit A2 das System aller dieser Zahlen
 2, mit
A1 das System aller anderen Zahlen
2, mit
A1 das System aller anderen Zahlen
 1; jede der
leßteren hat die Eigenschaft, daß im Laufe des Processes definitiv
x >
1; jede der
leßteren hat die Eigenschaft, daß im Laufe des Processes definitiv
x >
 1 wird, mithin ist
jede Zahl
1 wird, mithin ist
jede Zahl  1 kleiner
als jede Zahl
1 kleiner
als jede Zahl  2,
und folglich existirt eine Zahl
2,
und folglich existirt eine Zahl  ,
welche entweder die größte in A1 oder die
kleinste in A2 ist (§. 5. IV.). Das Erstere kann nicht der
Fall sein, weil x nie aufhört, zu wachsen, also ist
,
welche entweder die größte in A1 oder die
kleinste in A2 ist (§. 5. IV.). Das Erstere kann nicht der
Fall sein, weil x nie aufhört, zu wachsen, also ist
 die kleinste Zahl in
A2. Welche Zahl
die kleinste Zahl in
A2. Welche Zahl
 1 man nun auch
nehmen mag, so wird schließlich definitiv
1 man nun auch
nehmen mag, so wird schließlich definitiv
 1 < x
<
1 < x
<  sein, d.h. x
nähert sich dem Grenzwehrte
sein, d.h. x
nähert sich dem Grenzwehrte
 .
[pag. 23]
.
[pag. 23]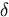 auch eine entsprechende Stelle
angeben, von welcher ab x sich um Weniger als
auch eine entsprechende Stelle
angeben, von welcher ab x sich um Weniger als
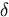 ändert, so nähert sich
x einem Grenzwehrt.''
ändert, so nähert sich
x einem Grenzwehrt.''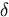 eine beliebige positive
Größe (d.h.
eine beliebige positive
Größe (d.h. 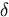 > 0), so
wird der Annahme zufolge ein Augenblick eintreten, von welchem ab
x sich um weniger als
> 0), so
wird der Annahme zufolge ein Augenblick eintreten, von welchem ab
x sich um weniger als 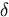 ändern wird, d.h. wenn x in diesem Augenblick den Wehrt
a besißt, so wird in der Folge stets x >
a -
ändern wird, d.h. wenn x in diesem Augenblick den Wehrt
a besißt, so wird in der Folge stets x >
a - 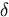 und x < a
+
und x < a
+ 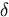 sein. Ich lasse nun einstweilen
die ursprüngliche Annahme fallen, und halte nur die soeben bewiesene
Thatsache fest, daß alle späteren Wehrte der Veränderlichen
x zwischen zwei angebbaren, endlichen Wehrten liegen. Hierauf
gründe ich eine doppelte Eintheilung aller reellen Zahlen. In das System
A2 nehme ich eine Zahl
sein. Ich lasse nun einstweilen
die ursprüngliche Annahme fallen, und halte nur die soeben bewiesene
Thatsache fest, daß alle späteren Wehrte der Veränderlichen
x zwischen zwei angebbaren, endlichen Wehrten liegen. Hierauf
gründe ich eine doppelte Eintheilung aller reellen Zahlen. In das System
A2 nehme ich eine Zahl
 2 (z.B.
a +
2 (z.B.
a + 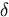 ) auf, wenn im Laufe
des Processes definitiv x <
) auf, wenn im Laufe
des Processes definitiv x <
 2 wird; in das
System A1 nehme ich jede nicht in A2
enthaltene Zahl auf; ist
2 wird; in das
System A1 nehme ich jede nicht in A2
enthaltene Zahl auf; ist
 1 eine solche
Zahl, so wird, wie weit auch der Proceß vorgeschritten sein mag, es noch
unendlich oft eintreten, daß x >
1 eine solche
Zahl, so wird, wie weit auch der Proceß vorgeschritten sein mag, es noch
unendlich oft eintreten, daß x >
 1 ist. Da jede Zahl
1 ist. Da jede Zahl
 1 kleiner ist als
jede Zahl
1 kleiner ist als
jede Zahl  2, so
giebt es eine völlig bestimmte Zahl
2, so
giebt es eine völlig bestimmte Zahl
 , welche diesen Schnit
(A1, A2) des Systems R hervorbingt, und
welch ich den oberen Grenzwehrt
[pag. 24]
der stets endlich bleibenden Veränderlichen x nennen will.
Ebenso wird durch das Verhalten der Veränderlichen x ein
zweiter Schnitt (B1, B2) des Systems R
hervorgebracht: eine Zahl ß1 (z.B. a -
, welche diesen Schnit
(A1, A2) des Systems R hervorbingt, und
welch ich den oberen Grenzwehrt
[pag. 24]
der stets endlich bleibenden Veränderlichen x nennen will.
Ebenso wird durch das Verhalten der Veränderlichen x ein
zweiter Schnitt (B1, B2) des Systems R
hervorgebracht: eine Zahl ß1 (z.B. a -
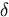 ) wird in B1
aufgenommen, wenn im Laufe des Processes definitiv x
> ß1 wird; jede andere, in
B2 aufzunehmende Zahl ß2 hat die
Eigenschaft, daß niemals definitiv x >
ß2, also immer noch unendlich oft x <
ß2 wird; die Zahl ß, durch welche dieser Schnitt
hervorgebracht wird, heiße der untere Grenzwehrt der
Veränderlichen x. Die beiden Zahlen
) wird in B1
aufgenommen, wenn im Laufe des Processes definitiv x
> ß1 wird; jede andere, in
B2 aufzunehmende Zahl ß2 hat die
Eigenschaft, daß niemals definitiv x >
ß2, also immer noch unendlich oft x <
ß2 wird; die Zahl ß, durch welche dieser Schnitt
hervorgebracht wird, heiße der untere Grenzwehrt der
Veränderlichen x. Die beiden Zahlen
 , ß sind offenbar auch durch
die folgende Eigenschaft characterisirt: ist
, ß sind offenbar auch durch
die folgende Eigenschaft characterisirt: ist
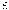 eine beliebig kleine positive
Größe, so wird stets definitiv x <
eine beliebig kleine positive
Größe, so wird stets definitiv x <
 +
+
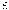 und x > ß -
und x > ß -
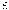 , aber niemals wird definitiv
x <
, aber niemals wird definitiv
x <  -
-
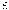 , und niemals definitiv x
> ß +
, und niemals definitiv x
> ß + 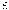 . Nun sind zwei
Fälle möglich. Sind
. Nun sind zwei
Fälle möglich. Sind  und
ß verschieden von einander, so ist nothwendig
und
ß verschieden von einander, so ist nothwendig
 > ß, weil stets
> ß, weil stets
 2 >
ß1 ist; die Veränderliche x oscillirt und
erleidet, wi weit der Proceß auch vorgeschritten sein mag, immer noch
Aenderungen, deren Betrag den Wehrt
(
2 >
ß1 ist; die Veränderliche x oscillirt und
erleidet, wi weit der Proceß auch vorgeschritten sein mag, immer noch
Aenderungen, deren Betrag den Wehrt
( - ß) -
2
- ß) -
2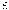 übetrifft, wo
übetrifft, wo
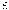 eine beliebig kleine positive
Größe bedeutet. Die ursprüngliche Annahme, zu der ich erst
jeßt zurückkehre, steht aber im Widerspruch mit dieser Consequenz;
es bleibt daher nur der zweite Fall
eine beliebig kleine positive
Größe bedeutet. Die ursprüngliche Annahme, zu der ich erst
jeßt zurückkehre, steht aber im Widerspruch mit dieser Consequenz;
es bleibt daher nur der zweite Fall
 = ß übrig, und da
schon bewiesen ist, daß, wie klein auch die positive Größe
= ß übrig, und da
schon bewiesen ist, daß, wie klein auch die positive Größe
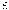 sien mag, immer definitiv
x <
sien mag, immer definitiv
x <  +
+
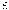 und x > ß -
und x > ß -
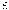 wird, so nähert sich
x dem Grenzwehrt
wird, so nähert sich
x dem Grenzwehrt  , was
zu beweisen war.
, was
zu beweisen war.