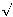 2 aus der Einheit gebildet? ist es
nicht so:
2 aus der Einheit gebildet? ist es
nicht so:
| 1 | = | 1 | × | 1 |
| 6 | 2 | 3 |
| 3 | = | 1 + 1 + 1 | ? |
| 4 | 1 + 1 + 1 + 1 |
| ,, | 3 | × a = ( | a | ) × 3'' und ,, | 3 | × a = | a + a + a | '' wählen? |
| 4 | 4 | 4 | a + a + a + a |
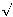 2 aus der Einheit gebildet? ist es
nicht so:
2 aus der Einheit gebildet? ist es
nicht so:
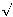 2 =
2 =
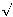 (1 + 1) ?
(1 + 1) ?
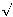 2
× a =
2
× a = 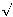 (a + a)'' ? ! !
(a + a)'' ? ! !| a | + | c | = | ad + bc | , |
| b | d | bd |
| ,,Ein | Kilo | Waare | kostet | a geldeinheiten |
| 10 | ,, | ,, | ,, | 10 × a |
| 12 | ,, | ,, | ,, | 10 × a + 2 × a |
| 10½ | ,, | ,, | ,, | 10 × a + soviel als ½ Kilo kostet, d.h. |
| 10 × a + a : 2 |
| aus | ax = b, | |
| wegen | max = mb, folgt: (b,a) = (mb, ma). | |
| Ferner: | aus | ax = b und cy = d, |
| wegen | cax = cb, und acy = ad, und ac = ca | |
| folgt: | cax + cay = cb + ad, und | |
| wegen | mx + my = m(x + y), | |
| folgt: | ca(x + y) | = cb + ad, d.h. x + y = (cb + ad, ca), |