EEN NIEUWE THEORIE VAN HET ONMEETBARE GETAL,
door
Dr. P.J.H. Baudet
Aanvullende gegevens:
Artikel in: Christiaan Huygens I (1921-22), pp.
33-47. De beide voetnoten (hier opgenomen als eindnoten) waren beiden met
het nummer 1 aangeduid.
Wij meenen, dat de hier medegedeelde theorie van het
onmeetbare getal reden van bestaan heeft naast de bekende theorieën
van DEDEKIND, CANTOR en WEIERSTRASS. In verschillende opzichten,
inzonderheid de aansluiting aan de meetbare getallen en
het bewijs der stelling van de onderste en bovenste grens, biedt
de nieuwe theorie voordeelen boven de bestaande theorieën.
§ 1. Grondeigenschappen der niet-negatieve
meetbare
getallen. Wij denken ons achtereenvolgens ingevoerd de natuurlijke
getallen, het getal nul en de positieve meetbare
getallen en
onderstellen, dat voor die getallen de rekenregels (zoowel betreffende
gelijkheden als ongelijkheden) zijn aangetoond. De rekenregels
berusten op het volgende:
I. Grondeigenschappen der rechtstreeksche
verbindingen.
a. Er is een verbinding ,,optelling'', die uit
ieder tweetal (al of niet verschillende) getallen van het stelsel
één en slechts één getal van dat stelsel doet
vinden (mogelijkheid en ondubbelzinnigheid der optelling).
b. a + b = b + a (commutatieve
eigenschap).
c. (a + b) + c = a +
(b + c) (associatieve eigenschap).
d. Er is een getal 0, waarvoor geldt
a + 0 = a (modulaire eigenschap).
e. Mogelijkheid en ondubbelzinnigheid van een
tweede verbinding ,,vermenigvuldiging''.
f. a . b = b . a (commutatieve
eigenschap).
g. (a . b) . c = a .
(b . c) (associatieve eigenschap).
h. (a + b) . c = a . c + b .
c (distributieve eigenschap).
i. Er is een getal 1, waarvoor geldt 1 .
a = a (modulaire eigenschap).
[pag. 34]
II. Grondeigenschappen der volgorde en der
omgekeerde verbindingen.
a. Voor ieder twee getallen a en
b van het stelsel bestaat één en slechts
één der drie volgende betrekkingen:
a = b,
a > b (ook te schrijven als b <
a),
a < b (ook te schrijven als b >
a).
b. Is a > 0 en b > 0,
dan is a + b > 0 (som van twee positieve getallen is
positief).
c. Is a > 0 en b > 0,
dan is a . b > 0 (product van twee positieve getallen is
positief).
d. Is b > 0, dan is a +
b > a.
e. Is a > b, dan bestaat
er een zoodanig getal x, dat a = b + x en x >
0 is (mogelijkheid der aftrekking van een kleiner getal van een
grooter).
f. Is b niet 0, dan bestaat er een
zoodanig getal x, dat x . b = 1 is (mogelijkheid der
deeling op 1, mits niet door 0).
g. Is a een gegeven getal, dan kan
men steeds een som van zooveel termen 1 vormen, dat die > a is
(dus een natuurlijk getal vormen, dat > a is).
§ 2. Definitie der reëele
getallen. Wij denken ons verzamelingen van meetbare getallen en
onderstellen steeds, dat de beschouwde getalverzamelingen niet leeg
zijn, d.w.z. dat zij minsten één getal bevatten.
Tot en met § 6 verstaan wij onder ,,getal'' zonder meer steeds ,,meetbaar
getal > 0''
Twee getalverzamelingen U en V
noemen wij dan en alleen dan gelijk, als ieder getal, dat grooter
dan een getal van U is, ook grooter is dan een of ander getal van V en
omgekeerd. Het praedicaat ,,gelijk'' is commutatief, d.w.z. U =
V beteekent hetzelfde als V = U.
Gelijk beteekent dus niet, dat U en
V identiek zijn
(d.w.z. uit dezelfde getallen bestaan), hoewel omgekeerd ,,identiek'' wel
,,gelijk'' ten gevoge heeft; m.a.w. een getalverzameling is aan zich zelf gelijk.
Een voorbeeld van gelijk getalverzamelingen is het volgende: de verzameling der
natuurlijke getallen > 1, die der getallen > 1 en de verzameling, die
alleen uit het getal 1 bestaat.
[pag. 35]
Zijn U, V en W getalverzamelingen, waarvoor geldt
U = V en V = W, dan is U = W; m.a.w. twee getalverzamelingen, die aan een
zelfde derde getalverzameling gelijk zijn, zijn ook onderling gelijk (transitiviteit
der gelijkheid).
Is nl. d grooter dan een getal van
U, dan is d ook grooter dan een getal van V
(wegens U = V) en dus ook grooter dan een getal van W
(wegens v = w). Evenzoo blijkt het omgekeerde.
De commutativiteit en transitiviteit van het praedicaat
,,gelijk'' maken, dat wij de getalverzamelingen, die aan een
getalverzameling U gelijk zijn, vereenigen kunnen tot een klasse van
getalverzamelingen, waarvan iedere twee onderling gelijk zijn (in welke
klasse dus door U geen andere rol gespeeld wordt dan door iedere
andere getalverzameling dier klasse). Zulk een klasse van gelijke
getalverzamelingen wordt een reëel getal
genoemd. Ieder getalverzameling der klasse kan dienen om het reëele
getal aan te wijzen en is dus als representant van het
reëele getal te beschouwen.
Een getalverzameling, die slechts uit
één enkel getal bestaat, noemen we
enkelvoudig; een enkelvoudige getalverzameling wijzen
we aan door het getal, waaruit ze bestaat. Een klasse van gelijke
getalverzamelingen kan geen twee (verschillende) enkelvoudige
getalverzamelingen bevatten. Is toch a > b, dan is a
grooter dan een getal der verzameling b (nl. > b), maar
niet grooter dan een getal van de verzameling a, zoodat de
enkelvoudige getalverzamelingen a en b ongelijk zijn en dus
niet tot dezelfde klasse behooren.
Een reëel getal, dat een enkelvoudige
getalverzameling a als representant heeft, wordt met het getal a
geïdentificeerd; d.w.z. het getal a (niet als verzameling
beschouwd, maar als meetbaar getal in de vroegere beteekenis) wordt onder de
representanten van het reëele getal opgenomen. Op deze wijze verschijnen
de aanvankelijk aanwezige getallen (meetbare getallen > 0) als
bijzondere gevallen der nieuw gevormde getallen.
Een reëel getal, waarbij onder de
representanten geen enkelvoudige getalverzameling voorkomt, heet
onmeetbaar. Ook de getalverzamelingen, die dit getal
representeeren, noemen we onmeetbaar. Een onmeetbare getalverzameling
is dus een getalverzameling, die niet aan een enkelvoudige getalverzameling
gelijk is. Zulk een getalverzameling bevat steeds oneindig veel getallen;
[pag. 36]
immers een verzameling van een eindig aantal getallen is gelijk aan de
verzameling, die alleen uit het kleinste dier getallen bestaat.
Een voorbeeld van een onmeetbare getalverzameling
levert de verzameling V der getallen, waarvan het kwadraat > 2 is.
Deze kan niet aan enkelvoudige getalverzameling a gelijk zijn. Is toch
a2 < 2, dan is a + ¼(2 -
a2) grooter dan a, maar niet grooter dan
een getal van V (daar het kwadraat van
a2 < 2, dan is a + ¼(2 -
a2) kleiner dan 2 is). Is
a2 > 2, dan is a grooter dan het getal
[a2 + 2]/2a van V maar niet
grooter dan a. Verder is a2 = 2
onmogelijk.
Men kan bij een gegeven getalverzameling U en
een gegeven getal e steeds een getal d vormen, zoodanig dat niet beneden d,
maar wel beneden d + e een getal van V gelegen is. Immers in de reeks
getallen 0, e, 2e, 3e, enz. komt men eindelijk op
een getal dat een getal van V overtreft; voor d kan men nu
nemen het grootste der getallen 0, e, 2e, ...., dat geen
getal van V overtreft.
§ 3. Optelling van reëele
getallen. Onder de som U + V der getalverzamelingen U
en V verstaan we de verzameling der getallen, die de som zijn van een getal van
U en een getal van V
Is U = U', dan is U + V = U' + V.
Is toch d > u + v, waarin
u een getal van U en v een getal van
V is, dat is d - v > u. Wegens U = U'
is d - v dus ook grooter dan een getal u' van
U', dus d > u' + v. Is omgekeerd d
> u' + v, dan is er ook een getal u van U,
waarvoor d > u + v geldt.
Evenzoo is U + V = U + V' als V =
V' is, zoodat de som van twee getalverzamelingen gelijk blijft, als
men de eene of andere dier verzamelingen door een daaraan gelijke
vervangt..
Deze eigenschap maakt, dat men de definitie der
optelling van de getalverzamelingen U en V op de daardoor gerepresenteerde
reëele getallen  en ß
kan overdragen. De som
en ß
kan overdragen. De som
 + ß is dat het reëele
getal, dat gerepresenteerd wordt door U + V, waarin U een representant van
+ ß is dat het reëele
getal, dat gerepresenteerd wordt door U + V, waarin U een representant van
 en V een representant van ß
is; welke representant men daarvoor kiest, heeft op het gevormde
reëele getal
en V een representant van ß
is; welke representant men daarvoor kiest, heeft op het gevormde
reëele getal  + ß geen
invloed.
+ ß geen
invloed.
Is  meetbaar, dan kan men voor U het enkele getal
meetbaar, dan kan men voor U het enkele getal
 nemen. U + V wordt
dan gevormd door de getallen
nemen. U + V wordt
dan gevormd door de getallen  +
v, waarin v ieder getal van V zijn kan. Is ook
ß meetbaar, dan kan met ook
[pag. 37]
voor V een enkelvoudige verzameling nemen en bestaat U +
V uit het enkele getal
+
v, waarin v ieder getal van V zijn kan. Is ook
ß meetbaar, dan kan met ook
[pag. 37]
voor V een enkelvoudige verzameling nemen en bestaat U +
V uit het enkele getal  +
ß, waarbij de optelling de oude beteekenis (optelling van meetbare
getallen) heeft. Zijn
+
ß, waarbij de optelling de oude beteekenis (optelling van meetbare
getallen) heeft. Zijn  en
ß beide meetbaar, dan voert dus de nieuwe definitie van optelling tot
dezelfde uitkomst als de oude definitie. Hiermede is aangetoond, dat de
oude optelling als bijzonder geval in de nieuwe optelling ligt opgesloten. Dit
beteekent de ondubbelzinnigheid der optelling, dus de geldigheid der
grondeigenschap Ia.
en
ß beide meetbaar, dan voert dus de nieuwe definitie van optelling tot
dezelfde uitkomst als de oude definitie. Hiermede is aangetoond, dat de
oude optelling als bijzonder geval in de nieuwe optelling ligt opgesloten. Dit
beteekent de ondubbelzinnigheid der optelling, dus de geldigheid der
grondeigenschap Ia.
De juistheid der grondeigenschappen Ib, c en
d blijkt onmiddelijk uit de overeenkomstige eigenschappen voor de
meetbare getallen. Zijn toch U, V en W resp.
representanten der reëele getallen
 , ß en
, ß en
 , dan wordt
(
, dan wordt
( + ß) +
+ ß) +
 gerepresenteerd door de
getalverzameling (U + V) + W gevormd door de getallen
(u + v) + w; evenzoo wordt
gerepresenteerd door de
getalverzameling (U + V) + W gevormd door de getallen
(u + v) + w; evenzoo wordt
 + (ß +
+ (ß +
 ) gerepresenteerd door
U + (V + W), bestaande uit de getallen u +
(v + w), die ook als (u + v) + w te schrijven
zijn (grondeigenschap Ic). Verder wordt
) gerepresenteerd door
U + (V + W), bestaande uit de getallen u +
(v + w), die ook als (u + v) + w te schrijven
zijn (grondeigenschap Ic). Verder wordt
 + 0, waarin
+ 0, waarin
 door U gerepresenteerd
is, gerepresenteerd door de verzameling der getallen u + 0 =
u, dus eveneens door U, zoodat
door U gerepresenteerd
is, gerepresenteerd door de verzameling der getallen u + 0 =
u, dus eveneens door U, zoodat
 + 0 =
+ 0 =
 is (grondeigenschap IId).
De juistheid van Ib is zoo doorzichtig, dat we daarover verder niets
behoeven te zeggen.
is (grondeigenschap IId).
De juistheid van Ib is zoo doorzichtig, dat we daarover verder niets
behoeven te zeggen.
§ 4. Vermenigvuldiging van reëele
getallen. Onder het product U . V der getalverzamelingen
U en V verstaan we de verzameling der getallen, die het product zijn
van een getal u van U en een getal v van V.
Is U = U', dan is U . V = U' . V.
Is nl. d > uv en v = 0,
dan is ook d > uv'. Is d > uv en
v > 0, dan is d/v > u. Wegens
U = U' is dan d/v ook grooter dan een getal
u' van U', dus d > u'v.
Evenzoo besluit men uit V = V' tot U .
V = U . V', waaruit op geheel dezelfde wijze als bij de optelling, blijkt,
dat men de vermenigvuldiging van de getalverzamelingen op de daardoor
gerepresenteerde reëele getallen kan overdragen.
Is  meetbaar en is V een representant van ß, dan wordt
meetbaar en is V een representant van ß, dan wordt
 . ß door de verzameling der
getallen
. ß door de verzameling der
getallen  . v
gerepresenteerd. Door ook ß meetbaar te nemen blijkt weer, dat bij
twee meetbare getallen de nieuwe definitie van vermenigvuldiging tot dezelfde
uitkomst voert als de oude. Hieruit blijkt de geldigheid der
grondeigenschap Ie.
[pag. 38]
. v
gerepresenteerd. Door ook ß meetbaar te nemen blijkt weer, dat bij
twee meetbare getallen de nieuwe definitie van vermenigvuldiging tot dezelfde
uitkomst voert als de oude. Hieruit blijkt de geldigheid der
grondeigenschap Ie.
[pag. 38]
De grondeigenschappen If, g, hen i
volgen weer uit de overeenkomstige eigenschappen voor de meetbare getallen.
Zoo wordt b.v. ( + ß) .
+ ß) .
 (met U, V, W resp. als
representanten van
(met U, V, W resp. als
representanten van  , ß,
, ß,
 ) gerepresenteerd door de
verzameling der getallen (u + v) . w en
) gerepresenteerd door de
verzameling der getallen (u + v) . w en
 .
.
 + ß .
+ ß .
 door de verzameling der getallen
u . w + v . w'. We laten het aan den lezer over de gelijkheid van
beide verzamelingen af te leiden.
door de verzameling der getallen
u . w + v . w'. We laten het aan den lezer over de gelijkheid van
beide verzamelingen af te leiden.
§ 5. Volgorde der reëele
getallen. Zijn U en V twee getalverzamelingen, dan
zegt men, dat U > V is, als er een getal d van U bestaat, dat een getal v
van V overtreft, maar geen enkel getal van U overtreft; men schrijft dan
ook V < U.
Is U = U' en U > V, dan is ook U' >
V.
Is nl. d > v en heeft U geen getal
< d, dan volgt uit U = U', dat ook U' geen getal
< d bevat.
Is V = V' en U > V, dan is ook U' >
V'.
Immers, heeft U geen getal < d en
is d grooter dan een getal van V, dan is d ook
grooter dan een getal van V'.
Uit deze eigenschappen blijkt weer, dat het
praedicaat ,,grooter'' van de getalverzamelingen U en V op de daardoor
gerepresenteerde reëele getallen  en ß kan worden
overgedragen.
en ß kan worden
overgedragen.
Zijn  en ß beide meetbaar, dan nemen we voor U het enkele
getal
en ß beide meetbaar, dan nemen we voor U het enkele
getal  en voor V het
enkele getal ß. Is dan
en voor V het
enkele getal ß. Is dan  > ß in de oude beteekenis, dan heeft U niet, maar
V wel een getal, dat door
> ß in de oude beteekenis, dan heeft U niet, maar
V wel een getal, dat door
 wordt overtroffen. Men heeft dus
U > V, zoodat ook in de nieuwe beteekenis
wordt overtroffen. Men heeft dus
U > V, zoodat ook in de nieuwe beteekenis
 > ß is.
> ß is.
Is U > V, dan heeft men niet U = V, evenmin als
U < V. Is nl. d > v en is voor ieder getal u van
U aan d < u voldaan, dan strijdt dit met de
definitie van U = V; is e grooter dan een getal u
van U, dan is e > d, dus e > v, dus niet aan de
definitie van U < V voldaan. Hieruit blijkt, dat men niet
gelijktijdig twee der gevallen  =
ß,
=
ß,  > ß,
> ß,
 < ß hebben kan. Daar
uit de definitie onmiddelijk te zien is, dat, als niet aan U = V voldaan
is, U > V of U < V is, doet zich steeds
één der drie gevallen
< ß hebben kan. Daar
uit de definitie onmiddelijk te zien is, dat, als niet aan U = V voldaan
is, U > V of U < V is, doet zich steeds
één der drie gevallen
 = ß,
= ß,
 > ß,
> ß,
 > ß voor. Hiermede is
de grondeigenschap IIa aangetoond.
> ß voor. Hiermede is
de grondeigenschap IIa aangetoond.
Is het reëele getal
 door de getalverzameling
U gerepresenteerd, dan wil
door de getalverzameling
U gerepresenteerd, dan wil
 > 0 zeggen, dat er een positief
getal d is, beneden welk geen getal van U gelegen is; om dit te bewijzen
neme men als representant van het getal 0 de verzameling, die alleen uit het
getal 0 bestaat. Is ook ß > 0, dan is er ook een positief
[pag. 39]
getal e, beneden welk geen getal van V (representant van
ß) gelegen is. Ieder getal van U + V en ieder getal van U .
V is dan grooter dan het positieve getal d + e resp. d .
e, zoodat
> 0 zeggen, dat er een positief
getal d is, beneden welk geen getal van U gelegen is; om dit te bewijzen
neme men als representant van het getal 0 de verzameling, die alleen uit het
getal 0 bestaat. Is ook ß > 0, dan is er ook een positief
[pag. 39]
getal e, beneden welk geen getal van V (representant van
ß) gelegen is. Ieder getal van U + V en ieder getal van U .
V is dan grooter dan het positieve getal d + e resp. d .
e, zoodat  + ß en
+ ß en
 . ß beide > 0 zijn.
Hiermede zijn de grondeigenschappen IIb en c
aangetoond.
. ß beide > 0 zijn.
Hiermede zijn de grondeigenschappen IIb en c
aangetoond.
Zij ß > 0 en e een positief
getal, beneden welk geen getal van V gelegen is. Zooals in § 2
gebleken is, kan men een getal d bepalen, zoodanig, dat niet beneden
d, maar wel beneden d + e een getal der verzameling
U (representant van  )
gelegen is. Voor ieder getal u van U en ieder getal
v van V geldt u > d, v >
e, dus u + v > d + e. Bijgevolg heeft U +
V niet, maar U wel een getal, dat door d + e wordt
overtroffen, zoodat U + V > V, dus
)
gelegen is. Voor ieder getal u van U en ieder getal
v van V geldt u > d, v >
e, dus u + v > d + e. Bijgevolg heeft U +
V niet, maar U wel een getal, dat door d + e wordt
overtroffen, zoodat U + V > V, dus
 + ß >
+ ß >
 is. Hiermede is de
grondeigenschap IId bewezen.
is. Hiermede is de
grondeigenschap IId bewezen.
We merken nog op, dat ieder reëel getal,
zooals dat in § 2 gedefiniëerd is, > 0 is. Daar
later ook reëele getallen ingevoerd worden, die < 0 (negatief) zijn, kan het
stelsel als dat der niet-negatieve reëele getallen worden
aangeduid.
§ 6. Aftrekking en deeling van reëele
getallen. Zij  > ß en
e een getal, dat grooter is dan een getal v van V
(representant van ß) en < u voor ieder getal
u van U (representant van
> ß en
e een getal, dat grooter is dan een getal v van V
(representant van ß) en < u voor ieder getal
u van U (representant van
 ). We vormen de verzameling
U - V der getallen u - d, waarbij we voor u ieder
getal van U nemen en voor d ieder getal, dat geen enkel
getal van V overtreft. Men heeft dan u > e >
d, dus u - d > e - d > 0. Bijgevolg representeert
U - V een positief reëel getal
). We vormen de verzameling
U - V der getallen u - d, waarbij we voor u ieder
getal van U nemen en voor d ieder getal, dat geen enkel
getal van V overtreft. Men heeft dan u > e >
d, dus u - d > e - d > 0. Bijgevolg representeert
U - V een positief reëel getal
 . De verzameling (U - V) +
V bestaat uit de getallen u - d + v = u + (v - d). Een getal
f, dat grooter is dan een getal u + (v - d) is, is ook grooter
dan u. Is omgekeerd f > u, dan bepalen we het getal
d zoo, dat niet beneden d, maar wel beneden d + (f -
u) een getal v van V gelegen is (zie § 2); men
heeft dan d + (f - u) > v, dus f - u > v - u, dus f > u
+ (v - d).
. De verzameling (U - V) +
V bestaat uit de getallen u - d + v = u + (v - d). Een getal
f, dat grooter is dan een getal u + (v - d) is, is ook grooter
dan u. Is omgekeerd f > u, dan bepalen we het getal
d zoo, dat niet beneden d, maar wel beneden d + (f -
u) een getal v van V gelegen is (zie § 2); men
heeft dan d + (f - u) > v, dus f - u > v - u, dus f > u
+ (v - d).
Hieruit besluit men tot (U - V) + V = U, dus
tot  + ß =
+ ß =
 , waarmede de grondeigenschap
IIe bewezen is.
, waarmede de grondeigenschap
IIe bewezen is.
Zij ß > 0, V een representant van
ß en 1/V de (niet-leege)
verzameling der getallen 1/d,
waarin men voor d ieder positief getal neemt, beneden welk geen
getal van V gelegen is. De verzameling
1/V.V bestaat uit de
getallen 1/d.v =
v/d. Daar
v/d > 1 is,
zal een
[pag. 40]
getal e, dat > v/d is,
ook > 1 zijn. Is omgekeerd e > 1, dan kan men v en
d zoo kiezen, dat e ook >
v/d is; daartoe neme men voor
d het grootste der getallen
d1,
d1 + (e -
1)d1,
d1 + 2(e -
1)d1,
d1 + 3(e -
1)d1, . . . .,
beneden welk geen getal van V gelegen is, waarin
d1 een bepaald positief getal is, beneden welk geen
getal van V ligt; is dan v een beneden
d + (e - 1)d1 gelegen getal
van V, dan heeft men:
v/d <
[d + (e -
1)d1]/d = 1 + (e -
1)d1/d < 1 + (e - 1) = e,
dus v/d < e.
Hieruit besluit men, dat de verzameling
1/V.V gelijk is aan de
enkelvoudige verzameling 1. Representeert
1/V het reëele getal
 , dan is dus
, dan is dus
 ß = 1. Hiermede is de
grondeigenschap IIf aangetoond.
ß = 1. Hiermede is de
grondeigenschap IIf aangetoond.
De grondeigenschap IIg ten slotte geeft geen
enkele moeilijkheid. Een natuurlijk getal n toch, dat grooter is dan een
getal der verzameling U, die het reëele getal
 representeert, is >
representeert, is >
 ; immers n overtreft een
getal van U, maar geen getal der enkelvoudige verzameling
n.
; immers n overtreft een
getal van U, maar geen getal der enkelvoudige verzameling
n.
We merken verder nog op, dat tusschen ieder
tweetal verschillende reëele getallen oneindig veel meetbare en oneindig
veel onmeetbare getallen gelegen zijn. Het bewijs hiervan laten we aan den
lezer over.
§ 7. Stelling van de onderste en bovenste
grens. Zij V een verzameling van (niet-negatieve)
reëele getallen. Onder de onderste grens g van
V verstaat men een getal 1)
met de eigenschappen, 1°. dat V geen getal < g bevat en 2°.
dat V voor elk getal h > g wel een getal < h bevat. We merken op,
dat geen twee getallen g en g' aan deze definitie kunnen voldoen; is
nl. g < g', dan heeft V volgens 1°. (toegepast op de
onderste grens g') geen getal < g' en volgens 2°.
(toegepast op de onderste grens g) wel een getal <
g'.
Een verzameling van (niet-negatieve) reëele
getallen heeft een onderste grens.
[pag. 41] Daartoe beschouwen we de verzameling
W der meetbare getallen, die ontstaat door ieder getal van
V door een representeerende verzameling van meetbare getallen te
vervangen en al deze verzamelingen tot één verzameling te
vereenigen (dus de verzameling te vormen van meetbare getallen, die tot
minstens één der bedoelde verzamelingen behooren). Deze
verzameling representeert een reëel getal g.
Is nu  een
getal van V en U de verzameling van meetbare getallen, die
een
getal van V en U de verzameling van meetbare getallen, die
 representeert, dan behoort ieder
getal van U ook tot W; er is dus een meetbaar getal te
vinden, dat een getal van U, maar geen enkel getal van W
overtreft, zoodat niet aan U < W, dus niet aan
representeert, dan behoort ieder
getal van U ook tot W; er is dus een meetbaar getal te
vinden, dat een getal van U, maar geen enkel getal van W
overtreft, zoodat niet aan U < W, dus niet aan
 < g voldaan is. Hieruit
blijkt, dat g aan het eerste deel der definitie van onderste grens
voldoet.
< g voldaan is. Hieruit
blijkt, dat g aan het eerste deel der definitie van onderste grens
voldoet.
Is T de verzameling van meetbare getallen,
die het reëele getal h (h > g) representeert, dan is er
(blijkens T > W) een meetbaar getal d, dat een getal
w van W, maar geen enkel getal van T overtreft.
Dit getal w behoort tot een der getalverzamelingen, uit wier
samenvoeging W ontstaan is, b.v. tot de getalverzameling
U, die het getal  van
V representeert. Men heeft dan U < T, dus
van
V representeert. Men heeft dan U < T, dus
 < h, zoodat g
ook aan het tweede deel der definitie van onderste grens voldoet.
< h, zoodat g
ook aan het tweede deel der definitie van onderste grens voldoet.
We merken nog op, dat de onderste grens van een
verzameling V van meetbare getallen niets anders is dan het reëele getal,
dat door V gerepresenteerd wordt. We kunnen dan nl. de
getalverzamelingen, die door samenvoeging W opleveren, alle
enkelvoudig kiezen, waardoor W met V identiek
wordt.
Een verzameling V van reëele getallen
heet naar boven begrensd, als er een getal M bestaat, dat
grooter is dan ieder getal van V.
Een naar boven begrensde verzameling van
(niet-negatieve) reëele getallen heeft een bovenste grens.
Hierbij is onder de bovenste grens G
van V een zoodanig getal te verstaan, dat V geen getal > G bevat,
maar wel een getal > H, als H < G is.
De aanwezigheid der bovenste grens wordt bewezen
door de onderste grens G te vormen van de verzameling V'
der getallen, die grooter zijn dan ieder getal van V. Deze verzameling
is niet leeg, daar M er toe behoort. Een getal
 van V kan niet >
G zijn; anders zou nl. V' een getal
van V kan niet >
G zijn; anders zou nl. V' een getal
 ' <
' <
 bevatten (volgens het
[pag. 42]
tweede deel der definitie van onderste grens), in strijd met de definitie van
V'. Is H < G, dan is een tusschen H en
G gelegen getal K geen getal van V' en overtreft
dus niet ieder getal van V; derhalve bevat V een getal, dat
> K, dus > H is. Het getal G
voldoet dus aan de definitie van bovenste grens van V.
bevatten (volgens het
[pag. 42]
tweede deel der definitie van onderste grens), in strijd met de definitie van
V'. Is H < G, dan is een tusschen H en
G gelegen getal K geen getal van V' en overtreft
dus niet ieder getal van V; derhalve bevat V een getal, dat
> K, dus > H is. Het getal G
voldoet dus aan de definitie van bovenste grens van V.
§ 8. Afgeleide eigenschappen.
Doordat bewezen is, dat de grondeigenschappen van § 1 voor de (niet-
negatieve) reëele getallen gelden, is daarmede voor die getallen ook de
geldigheid vastgesteld der afgeleide eigenschappen, dit
zijn die eigenschappen, welke uit de grondeigenschappen kunnen worden
afgeleid, zonder dat men op de beteekenis van het begrip ,,getal'', dus op de
beteekenis der letters a, b, c, . . . . en der teekens +, ., > en <,
heeft in te gaan. Slechts heeft men te weten, dat = beteekend ,,is hetzelfde
getal als'', dus dat = het teeken is voor identificeering.
Bekend genoeg is hoe het rekenen met sommen en producten uit
de grondeigenschappen I wordt afgeleid, waarom we volstaan willen met de
voornaamste afgeleide eigenschappen te bewijzen, die op de volgorde, op
aftrekking of op deeling betrekking hebben.
 ) Is a > b en b >
c, dan is a > c (transitieve eigenschap der volgorde).
) Is a > b en b >
c, dan is a > c (transitieve eigenschap der volgorde).
Volgens IIe kan men x en y zoo bepalen,
dat voldaan is aan:
a = b + x, x > 0, b = c + y, y > 0;
hieruit leidt men af:
a = (c + y) + x = c + (y + x)
(waarin y + x > 0 is volgens IIb, dus a > c (volgens
IId).
Door herhaalde toepassing van
 ) vindt men eigenschappen als:
) vindt men eigenschappen als:
Is a > b, b > c, c > d, en d > e, dan is a > e.
ß) Is a > b, dan is a + c > b + c.
Bepaalt men nl. x zoo, dat a = b + x en x >
0 is, dan is:
a + c = (b + x) + c = (b + c) + x
dus a + c > b + c (volgens IId).
Door herhaalde toepassing van ß) vindt men eigenschappen
als:
Is a > b en b > c, dan is a + c > b + d.
Is a > b, c > d, en e > f, dan is a + c + e > b + d +
f. [pag. 43]
 ) Er is hoogstens
één getal x, dat aan a = b + x voldoet (ondubbelzinnigheid der
aftrekking).
) Er is hoogstens
één getal x, dat aan a = b + x voldoet (ondubbelzinnigheid der
aftrekking).
Immers, was x > y en a = b + x, a = b + y, dan
had men volgens ß) b + x > b + y, dus a > a, in strijd met
IIa. Men kan de eigenschap ook zoo uitdrukken, dat uit b + x = b + y
volgt x = y.
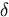 ) a . 0 = 0 (een
product, waarvan een der factoren 0 is, is 0).
) a . 0 = 0 (een
product, waarvan een der factoren 0 is, is 0).
Men heeft nl.:
a . b + 0 = a . b = a . (b + 0) = a . b + a . 0,
dus volgens  ) 0 = a . 0.
) 0 = a . 0.
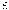 ) Is a > b en c >
0, dan is a . c > b . c.
) Is a > b en c >
0, dan is a . c > b . c.
Bepaalt men x zoo, dat a = b + x is (waarbij
wegens  ) vanzelf x > 0 is), dan
is:
) vanzelf x > 0 is), dan
is:
a . c = (b + x) . c = b . c + x . c;
volgens IIc is x . c > 0, dus (volgens IId) a . c > b .
c.
Door herhaalde toepassing van
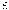 ) bewijst men eigenschappen als:
) bewijst men eigenschappen als:
Is a > 0, a > b en c > d > 0, dan is a . c > b . d.
Is a > 0, a > b, c > d > 0, en e > f > 0, dan is a . c . e
> b . d . f.
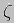 ) Is b niet 0, dan
bestaat er een zoodanig getal x, dat x . b = a (mogelijkheid der deeling, mits
niet door 0).
) Is b niet 0, dan
bestaat er een zoodanig getal x, dat x . b = a (mogelijkheid der deeling, mits
niet door 0).
Volgens IIf kan men nl. y zoo bepalen, dat
y . b = 1 is. Nu is:
(a . y) . b = a . (y . b) = a . 1 = a,
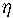 ) Is b niet 0, dan
bestaat er geen twee getallen x, die aan x . b = a voldoen (ondubbelzinnigheid
der deeling, mits niet door 0).
) Is b niet 0, dan
bestaat er geen twee getallen x, die aan x . b = a voldoen (ondubbelzinnigheid
der deeling, mits niet door 0).
Is toch y een getal, waarvoor y . b = 1 is, dan
volgt uit a = x . b:
a . y = (x . b) . y = x . (b . y) = x . 1 = x,
zoodat aan a = x . b door geen andere waarde van x dan a .
y kan worden voldaan. Men kan de eigenschap ook zoo uitdrukken, dat als b
niet 0, uit xb = yb volgt x = y.
Is b niet 0, dan volgt uit
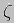 ) en
) en
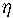 ), dat door x . b = a
één en slechts één getal x = a : b wordt aangewezen,
en dat dit getal x ook als a . (1 : b) te schrijven is. Hieruit vloeien
alle eigenschappen van quotiënten voort.
), dat door x . b = a
één en slechts één getal x = a : b wordt aangewezen,
en dat dit getal x ook als a . (1 : b) te schrijven is. Hieruit vloeien
alle eigenschappen van quotiënten voort.
 ) Is a . b = 0
en a niet 0, dan is b = 0.
) Is a . b = 0
en a niet 0, dan is b = 0.
Uit a . b = 0 volgt nl. in verband met
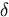 ) a . b = a . 0, dus in verband
met
) a . b = a . 0, dus in verband
met 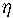 ) b = 0
[pag. 44].
) b = 0
[pag. 44].
Met 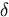 ) samengevat
drukt
) samengevat
drukt  ) uit, dat een product dan
en alleen dan 0 is, wanneer minstens één der factoren 0 is,
hetgeen natuurlijk zonder moeite tot een product van drie of meer factoren is
uit te breiden.
) uit, dat een product dan
en alleen dan 0 is, wanneer minstens één der factoren 0 is,
hetgeen natuurlijk zonder moeite tot een product van drie of meer factoren is
uit te breiden.
 ) Zijn a en b
twee gegeven getallen en is b > 0, dan kan men steeds een natuurlijk getal
vinden, waarvoor n . b > a is (eigenschap van Archimedes).
) Zijn a en b
twee gegeven getallen en is b > 0, dan kan men steeds een natuurlijk getal
vinden, waarvoor n . b > a is (eigenschap van Archimedes).
Volgens 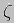 ) kan men nl.
x zoo bepalen, dat x . b = a is. Neemt men nu een natuurlijk
getal n > x (hetgeen volgens IIg mogelijk is), dan is volgens
) kan men nl.
x zoo bepalen, dat x . b = a is. Neemt men nu een natuurlijk
getal n > x (hetgeen volgens IIg mogelijk is), dan is volgens
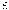 ) n . b > x . b, dus n . b
> a.
) n . b > x . b, dus n . b
> a.
Het bewijs van de genoemde afgeleide eigenschappen voor de
(niet-negatieve) reëele getallen behoeft dus niet geleverd te worden door
op de definitie der reëele getallen in te gaan, al zal dat bv. voor een
eigenschap als a . 0 = 0 niet de minste moeite kosten; is toch a
door de verzameling U van meetbare getallen gerepresenteerd en kiest men
als representant van het getal 0 de enkelvoudige verzameling 0, dan bestaat ook
de productverzameling uit het enkele getal 0
2).
§ 9. Invoering der negatieve getallen. Nadat het
stelsel der niet-negatieve reëele getallen gevormd is, wordt het
getalstelsel nog verder uitgebreid door de vorming van getallenparen (a,
b). Hierbij wordt gelijkheid van (a, b) en (c, d)
gedefiniëerd als a + d = c + d, waarna een reëel
getal gedefiniëerd wordt als een klasse van gelijke
getallenparen (waarbij de getallen, die gepaard worden, niet-negatieve
reëele getallen zijn); dit wordt weer door de commutativiteit en
transitiveit der gelijkheid mogelijk
[pag. 45]
gemaakt. Optelling en vermenigvuldiging worden gedefiniëerd door:
(a, b) + (c, d) = (a + b, c + d),
(a, b) . (c, d) = (ac + bd, ad + cb),
terwijl (a, b) > (c, d) beteekent, dat a + d > c + b is.
Deze definities kunnen weer worden overgedragen op de reëele getallen, die
door de getallenparen gerepresenteerd worden.
Verder heeft men nog de definitie (a, 0) = a,
waardoor de reeds aanwezige getallen in het nieuw gevormde stelsel worden
ondergebracht. Hieruit leidt men af, dat alle getallen van het nieuwe
stelsel, die niet reeds tot het oorspronkelijke stelsel behooren, negatief
zijn, zoodat men inderdaad het oorspronkelijke stelsel (dat van § 2-5)
als het stelsel der niet-negatieve reëele getallen kan aanduiden.
Een uitvoeriger behandeling van de invoering der negatieve getallen vindt men
in F. SCHUH, Leerboek der Theoretische Rekenkunde I, n°. 488-575 of
Leerboek der Elementaire Theoretische Rekenkunde I, n°. 396-470, waar de
getallen, die gepaard worden, aantallen (geheele getallen > 0) zijn,
hetgeen echter geen wezenlijk verschil maakt.
Voor het nieuw gevormde stelsel moeten de in § 1 genoemde
grondeigenschappen worden aangetoond, waarbij men nu echter IId en
e met voordeel vervangt door:
IId'. Is b > c, dan is a + b > a + c (de
eigenschap ß) van § 8).
IIe'. Voor ieder getal b bestaat er een getal x,
waarvoor b + x = 0 is (mogelijkheid der aftrekking van 0).
Zooals in § 6 voor de deeling geschied is, leidt men
hieruit af, dat iedere aftrekking mogelijk en ondubbelzinnig is en dat
men heeft: a - b = a + (-b).
Uit IId' leidt men IId af door c = 0 te
nemen.
Verder bewijst men IIe door op te merken dat wegens
IId' uit a > b volgt a + (-b) > b + (-b) = 0, dus a - b
> 0. Evenzoo leidt men uit a < b af, dat a - b < 0 is,
zoodat a - b positief of negatief is, al naar gelang a > b of a < b is.
In het bijzonder heeft men, dat -b (of 0 - b) negatief of
positief is, al naar gelang b positief of negatief is.
Eigenschappen als a . (-b) = -(a . b) en (-a) .
(-b) = a . b vloeien eveneens uit de grondeigenschappen voort en behoeven
[pag. 46]
dus niet afzonderlijk met behulp van getallenparen bewezen te worden (al zou dit
ook gemakkelijk te doen zijn). Men heeft nl.:
a(-b) = a(-b) + 0 = a(-b) + ab + (-ab) =
= a(-b + b) + (-ab) = a.0 + (-ab) = 0 + (-ab) = -ab,
(-a)(-b) = -(-a)b = -(-ab) = ab.
De stellingen betreffende de bovenste en onderste
grens (zie § 7) blijven doorgaan, zoo men ook ten aanzien van de
onderste grens een beperking maakt, nl., dat de verzameling V naar onderen
begrensd is, hetgeen zeggen wil, dat er een getal m is, dat kleiner is
dan ieder getal van V. Immers, door alle getallen van V met
-m te vermeerderen, ontstaat een verzameling van positieve getallen, die
een onderste grens g' heeft; g' + m is dan ten duidelijkste de
onderste grens van V. Is de verzameling V naar boven begrensd en
is  een bepaald getal van V, dan
vormen we de verzameling van getallen, die ontstaan door de getallen van
V, welke >
een bepaald getal van V, dan
vormen we de verzameling van getallen, die ontstaan door de getallen van
V, welke >  zijn, met
-
zijn, met
- te vermeerderen; is van deze
verzameling (die naar boven begrensd is en waarvan alle getallen > 0
zijn) G' de bovenste grens, dan is G' +
te vermeerderen; is van deze
verzameling (die naar boven begrensd is en waarvan alle getallen > 0
zijn) G' de bovenste grens, dan is G' +
 de bovenste grens van V.
de bovenste grens van V.
§ 10. Volledigheid van het stelsel der reëele
getallen. Houdt men vast aan de grondeigenschappen van § 1 en laat
men geen negatieve getallen toe, dan is aan het in § 2-5 gevormde stelsel
S der niet-negatieve reëele getallen geen enkel getal meer toe te
voegen, ten minste zoo men wil, dat na de toevoeging de begrippen ,,som'',
,,product'', en ,,grooter'' bij de reeds aanwezige getallen dezelfde gebleven
zijn.
Zij toch S' zulk een stelsel, dat S omvat en
a' een getal van S'. We vormen nu de verzameling V der
getallen van S, die > a' zijn. Die verzameling is niet leeg, daar
er volgens IIg een natuurlijk getal n bestaat, dat > a'
is, terwijl n een getal van S is. Bij gevolg heeft V een
(tot S behoorende) onderste grens, die we a noemen.
Nu is a' > a uitgesloten. Immers er zou dan een
positief getal a' - a en dus ook een positief getal
1/[a' - a] bestaan, waarna men een
natuurlijk getal m zou kunnen vormen, dat >
1/[a' - a] is. Het getal b =
a + 1/m zou dan > a en < a + (a' - a)
= a' zijn en tot S behooren. Wegens b > a ligt beneden
b een getal van
[pag. 47]
V, dus een getal, dat > a' is, zoodat ook b > a' is, in
strijd met b < a'.
Ook is a < a' uitgesloten. Men zou dan nl. weer een
tot S behoorend getal b kunnen vormen zoodanig, dat a' < b <
a is. Wegens b < a is b geen getal van V en is dus
b < a', in strijd met b > a'.
Daar noch aan a' > a, noch aan a' < a voldaan
is, besluit men uit IIa tot a' = a, hetgeen beteekent, dat
a' een getal van S is.
Laat men wel negatieve getallen toe, dan is het stelsel,
gevormd door alle reëele getallen, volledig in den zin, dat er niets
aan is toe te voegen met behoud der grondeigenschappen. Bij toevoeging van het
negatieve getal a' zou nl. ook het positieve getal -a' worden
toegevoegd, hetgeen gebleken is onmogelijk te zijn.
§ 11. Slotopmerking. In § 2 is
het reëele getal ingevoerd feitelijk als onderste grens van een verzameling
meetbare getallen > 0. Men kan natuurlijk ook de theorie
opbouwen met als grondslag het begrip bovenste grens. In de tweede alinea van
§ 2 moet dan ,,grooter'' vervangen worden door ,,kleiner''. Bovendien
heeft men dan nog toe te voegen, dat elke beschouwde getalverzameling naar
boven begrensd moet zijn. Daar deze toevoeging bij den gekozen opzet niet
noodig is, is hij ietwat eenvoudiger.
Ook zou men het onmeetbaar getal kunnen invoeren
nadat aan het stelsel der meetbare getallen > 0 de negatieve
meetbare eerst zijn toegevoegd. In dat geval moet men de getalverzamelingen
eenzijdig begrensd veronderstellen. Het nadeel van deze laatste volgorde van
invoering (bij deze theorie zoowel als bij die van DEDEKIND) is, dat de
vermenigvuldiging dan aanleiding geeft tot veel omhaal, zoodat de elegance
daarbij zeer zou lijden.
Voetnoten
1) In deze § heeft ,,getal'' de beteekenis van
,,niet-negatief reëel getal''.
2) Uit het oogpunt van den axiomatischen opbouw der
rekenkunde (waarbij getallen dingen zijn, die aan eenige als axioma's
vooropgestelde grondeigenschappen voldoen) is het van eenig belang, dat
ook 1 > 0 een afgeleide eigenschap is. Uit 1 < 0 toch zou
volgen 1 + 1 + ... + 1 < 0, hetgeen in strijd is met IIg.
Dat 1 niet < 0 is, bewijst men ook zonder IIg aldus: Uit 1 < 0 volgt
in verband met IIe het bestaan van een getal x > 0. In
verband met 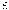 ) en
) en
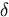 ) heeft men dan verder:
) heeft men dan verder:
x = 1.x < 0.x = 0,
dus x < 0, in strijd met x > 0.
Het is duidelijk, dat de omstandigheid, dat 1 > 0 uit de
grondeigenschappen is af te leiden, voor de invoering der onmeetbare getallen
van geenerlei beteekenis is, daar 1 > 0 een waarheid is, die men al kent, als
men tot de invoering der onmeetbare getallen overgaat.
 en ß
kan overdragen. De som
en ß
kan overdragen. De som
 + ß is dat het reëele
getal, dat gerepresenteerd wordt door U + V, waarin U een representant van
+ ß is dat het reëele
getal, dat gerepresenteerd wordt door U + V, waarin U een representant van
 en V een representant van ß
is; welke representant men daarvoor kiest, heeft op het gevormde
reëele getal
en V een representant van ß
is; welke representant men daarvoor kiest, heeft op het gevormde
reëele getal  + ß geen
invloed.
+ ß geen
invloed. meetbaar, dan kan men voor U het enkele getal
meetbaar, dan kan men voor U het enkele getal
 nemen. U + V wordt
dan gevormd door de getallen
nemen. U + V wordt
dan gevormd door de getallen  +
v, waarin v ieder getal van V zijn kan. Is ook
ß meetbaar, dan kan met ook
[pag. 37]
voor V een enkelvoudige verzameling nemen en bestaat U +
V uit het enkele getal
+
v, waarin v ieder getal van V zijn kan. Is ook
ß meetbaar, dan kan met ook
[pag. 37]
voor V een enkelvoudige verzameling nemen en bestaat U +
V uit het enkele getal  +
ß, waarbij de optelling de oude beteekenis (optelling van meetbare
getallen) heeft. Zijn
+
ß, waarbij de optelling de oude beteekenis (optelling van meetbare
getallen) heeft. Zijn  en
ß beide meetbaar, dan voert dus de nieuwe definitie van optelling tot
dezelfde uitkomst als de oude definitie. Hiermede is aangetoond, dat de
oude optelling als bijzonder geval in de nieuwe optelling ligt opgesloten. Dit
beteekent de ondubbelzinnigheid der optelling, dus de geldigheid der
grondeigenschap Ia.
en
ß beide meetbaar, dan voert dus de nieuwe definitie van optelling tot
dezelfde uitkomst als de oude definitie. Hiermede is aangetoond, dat de
oude optelling als bijzonder geval in de nieuwe optelling ligt opgesloten. Dit
beteekent de ondubbelzinnigheid der optelling, dus de geldigheid der
grondeigenschap Ia. , ß en
, ß en
 , dan wordt
(
, dan wordt
( + ß) +
+ ß) +
 gerepresenteerd door de
getalverzameling (U + V) + W gevormd door de getallen
(u + v) + w; evenzoo wordt
gerepresenteerd door de
getalverzameling (U + V) + W gevormd door de getallen
(u + v) + w; evenzoo wordt
 + (ß +
+ (ß +
 ) gerepresenteerd door
U + (V + W), bestaande uit de getallen u +
(v + w), die ook als (u + v) + w te schrijven
zijn (grondeigenschap Ic). Verder wordt
) gerepresenteerd door
U + (V + W), bestaande uit de getallen u +
(v + w), die ook als (u + v) + w te schrijven
zijn (grondeigenschap Ic). Verder wordt
 + 0, waarin
+ 0, waarin
 door U gerepresenteerd
is, gerepresenteerd door de verzameling der getallen u + 0 =
u, dus eveneens door U, zoodat
door U gerepresenteerd
is, gerepresenteerd door de verzameling der getallen u + 0 =
u, dus eveneens door U, zoodat
 + 0 =
+ 0 =
 is (grondeigenschap IId).
De juistheid van Ib is zoo doorzichtig, dat we daarover verder niets
behoeven te zeggen.
is (grondeigenschap IId).
De juistheid van Ib is zoo doorzichtig, dat we daarover verder niets
behoeven te zeggen. meetbaar en is V een representant van ß, dan wordt
meetbaar en is V een representant van ß, dan wordt
 . ß door de verzameling der
getallen
. ß door de verzameling der
getallen  . v
gerepresenteerd. Door ook ß meetbaar te nemen blijkt weer, dat bij
twee meetbare getallen de nieuwe definitie van vermenigvuldiging tot dezelfde
uitkomst voert als de oude. Hieruit blijkt de geldigheid der
grondeigenschap Ie.
[pag. 38]
. v
gerepresenteerd. Door ook ß meetbaar te nemen blijkt weer, dat bij
twee meetbare getallen de nieuwe definitie van vermenigvuldiging tot dezelfde
uitkomst voert als de oude. Hieruit blijkt de geldigheid der
grondeigenschap Ie.
[pag. 38] + ß) .
+ ß) .
 (met U, V, W resp. als
representanten van
(met U, V, W resp. als
representanten van  , ß,
, ß,
 ) gerepresenteerd door de
verzameling der getallen (u + v) . w en
) gerepresenteerd door de
verzameling der getallen (u + v) . w en
 .
.
 + ß .
+ ß .
 door de verzameling der getallen
u . w + v . w'. We laten het aan den lezer over de gelijkheid van
beide verzamelingen af te leiden.
door de verzameling der getallen
u . w + v . w'. We laten het aan den lezer over de gelijkheid van
beide verzamelingen af te leiden. en ß kan worden
overgedragen.
en ß kan worden
overgedragen. en ß beide meetbaar, dan nemen we voor U het enkele
getal
en ß beide meetbaar, dan nemen we voor U het enkele
getal  en voor V het
enkele getal ß. Is dan
en voor V het
enkele getal ß. Is dan  > ß in de oude beteekenis, dan heeft U niet, maar
V wel een getal, dat door
> ß in de oude beteekenis, dan heeft U niet, maar
V wel een getal, dat door
 wordt overtroffen. Men heeft dus
U > V, zoodat ook in de nieuwe beteekenis
wordt overtroffen. Men heeft dus
U > V, zoodat ook in de nieuwe beteekenis
 > ß is.
> ß is. =
ß,
=
ß,  > ß,
> ß,
 < ß hebben kan. Daar
uit de definitie onmiddelijk te zien is, dat, als niet aan U = V voldaan
is, U > V of U < V is, doet zich steeds
één der drie gevallen
< ß hebben kan. Daar
uit de definitie onmiddelijk te zien is, dat, als niet aan U = V voldaan
is, U > V of U < V is, doet zich steeds
één der drie gevallen
 = ß,
= ß,
 > ß,
> ß,
 > ß voor. Hiermede is
de grondeigenschap IIa aangetoond.
> ß voor. Hiermede is
de grondeigenschap IIa aangetoond. door de getalverzameling
U gerepresenteerd, dan wil
door de getalverzameling
U gerepresenteerd, dan wil
 > 0 zeggen, dat er een positief
getal d is, beneden welk geen getal van U gelegen is; om dit te bewijzen
neme men als representant van het getal 0 de verzameling, die alleen uit het
getal 0 bestaat. Is ook ß > 0, dan is er ook een positief
[pag. 39]
getal e, beneden welk geen getal van V (representant van
ß) gelegen is. Ieder getal van U + V en ieder getal van U .
V is dan grooter dan het positieve getal d + e resp. d .
e, zoodat
> 0 zeggen, dat er een positief
getal d is, beneden welk geen getal van U gelegen is; om dit te bewijzen
neme men als representant van het getal 0 de verzameling, die alleen uit het
getal 0 bestaat. Is ook ß > 0, dan is er ook een positief
[pag. 39]
getal e, beneden welk geen getal van V (representant van
ß) gelegen is. Ieder getal van U + V en ieder getal van U .
V is dan grooter dan het positieve getal d + e resp. d .
e, zoodat  + ß en
+ ß en
 . ß beide > 0 zijn.
Hiermede zijn de grondeigenschappen IIb en c
aangetoond.
. ß beide > 0 zijn.
Hiermede zijn de grondeigenschappen IIb en c
aangetoond. )
gelegen is. Voor ieder getal u van U en ieder getal
v van V geldt u > d, v >
e, dus u + v > d + e. Bijgevolg heeft U +
V niet, maar U wel een getal, dat door d + e wordt
overtroffen, zoodat U + V > V, dus
)
gelegen is. Voor ieder getal u van U en ieder getal
v van V geldt u > d, v >
e, dus u + v > d + e. Bijgevolg heeft U +
V niet, maar U wel een getal, dat door d + e wordt
overtroffen, zoodat U + V > V, dus
 + ß >
+ ß >
 is. Hiermede is de
grondeigenschap IId bewezen.
is. Hiermede is de
grondeigenschap IId bewezen. > ß en
e een getal, dat grooter is dan een getal v van V
(representant van ß) en < u voor ieder getal
u van U (representant van
> ß en
e een getal, dat grooter is dan een getal v van V
(representant van ß) en < u voor ieder getal
u van U (representant van
 ). We vormen de verzameling
U - V der getallen u - d, waarbij we voor u ieder
getal van U nemen en voor d ieder getal, dat geen enkel
getal van V overtreft. Men heeft dan u > e >
d, dus u - d > e - d > 0. Bijgevolg representeert
U - V een positief reëel getal
). We vormen de verzameling
U - V der getallen u - d, waarbij we voor u ieder
getal van U nemen en voor d ieder getal, dat geen enkel
getal van V overtreft. Men heeft dan u > e >
d, dus u - d > e - d > 0. Bijgevolg representeert
U - V een positief reëel getal
 . De verzameling (U - V) +
V bestaat uit de getallen u - d + v = u + (v - d). Een getal
f, dat grooter is dan een getal u + (v - d) is, is ook grooter
dan u. Is omgekeerd f > u, dan bepalen we het getal
d zoo, dat niet beneden d, maar wel beneden d + (f -
u) een getal v van V gelegen is (zie § 2); men
heeft dan d + (f - u) > v, dus f - u > v - u, dus f > u
+ (v - d).
. De verzameling (U - V) +
V bestaat uit de getallen u - d + v = u + (v - d). Een getal
f, dat grooter is dan een getal u + (v - d) is, is ook grooter
dan u. Is omgekeerd f > u, dan bepalen we het getal
d zoo, dat niet beneden d, maar wel beneden d + (f -
u) een getal v van V gelegen is (zie § 2); men
heeft dan d + (f - u) > v, dus f - u > v - u, dus f > u
+ (v - d). + ß =
+ ß =
 , waarmede de grondeigenschap
IIe bewezen is.
, waarmede de grondeigenschap
IIe bewezen is. , dan is dus
, dan is dus
 ß = 1. Hiermede is de
grondeigenschap IIf aangetoond.
ß = 1. Hiermede is de
grondeigenschap IIf aangetoond. representeert, is >
representeert, is >
 ; immers n overtreft een
getal van U, maar geen getal der enkelvoudige verzameling
n.
; immers n overtreft een
getal van U, maar geen getal der enkelvoudige verzameling
n. een
getal van V en U de verzameling van meetbare getallen, die
een
getal van V en U de verzameling van meetbare getallen, die
 representeert, dan behoort ieder
getal van U ook tot W; er is dus een meetbaar getal te
vinden, dat een getal van U, maar geen enkel getal van W
overtreft, zoodat niet aan U < W, dus niet aan
representeert, dan behoort ieder
getal van U ook tot W; er is dus een meetbaar getal te
vinden, dat een getal van U, maar geen enkel getal van W
overtreft, zoodat niet aan U < W, dus niet aan
 < g voldaan is. Hieruit
blijkt, dat g aan het eerste deel der definitie van onderste grens
voldoet.
< g voldaan is. Hieruit
blijkt, dat g aan het eerste deel der definitie van onderste grens
voldoet. van
V representeert. Men heeft dan U < T, dus
van
V representeert. Men heeft dan U < T, dus
 < h, zoodat g
ook aan het tweede deel der definitie van onderste grens voldoet.
< h, zoodat g
ook aan het tweede deel der definitie van onderste grens voldoet. van V kan niet >
G zijn; anders zou nl. V' een getal
van V kan niet >
G zijn; anders zou nl. V' een getal
 ' <
' <
 bevatten (volgens het
[pag. 42]
tweede deel der definitie van onderste grens), in strijd met de definitie van
V'. Is H < G, dan is een tusschen H en
G gelegen getal K geen getal van V' en overtreft
dus niet ieder getal van V; derhalve bevat V een getal, dat
> K, dus > H is. Het getal G
voldoet dus aan de definitie van bovenste grens van V.
bevatten (volgens het
[pag. 42]
tweede deel der definitie van onderste grens), in strijd met de definitie van
V'. Is H < G, dan is een tusschen H en
G gelegen getal K geen getal van V' en overtreft
dus niet ieder getal van V; derhalve bevat V een getal, dat
> K, dus > H is. Het getal G
voldoet dus aan de definitie van bovenste grens van V. ) Is a > b en b >
c, dan is a > c (transitieve eigenschap der volgorde).
) Is a > b en b >
c, dan is a > c (transitieve eigenschap der volgorde).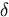 ) a . 0 = 0 (een
product, waarvan een der factoren 0 is, is 0).
) a . 0 = 0 (een
product, waarvan een der factoren 0 is, is 0).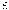 ) Is a > b en c >
0, dan is a . c > b . c.
) Is a > b en c >
0, dan is a . c > b . c.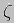 ) Is b niet 0, dan
bestaat er een zoodanig getal x, dat x . b = a (mogelijkheid der deeling, mits
niet door 0).
) Is b niet 0, dan
bestaat er een zoodanig getal x, dat x . b = a (mogelijkheid der deeling, mits
niet door 0).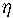 ) Is b niet 0, dan
bestaat er geen twee getallen x, die aan x . b = a voldoen (ondubbelzinnigheid
der deeling, mits niet door 0).
) Is b niet 0, dan
bestaat er geen twee getallen x, die aan x . b = a voldoen (ondubbelzinnigheid
der deeling, mits niet door 0). ) Is a . b = 0
en a niet 0, dan is b = 0.
) Is a . b = 0
en a niet 0, dan is b = 0. ) Zijn a en b
twee gegeven getallen en is b > 0, dan kan men steeds een natuurlijk getal
vinden, waarvoor n . b > a is (eigenschap van Archimedes).
) Zijn a en b
twee gegeven getallen en is b > 0, dan kan men steeds een natuurlijk getal
vinden, waarvoor n . b > a is (eigenschap van Archimedes).