Wat is wiskunde?
Geachte toehoorders. Toen U na het betreden van deze zaal op een van de stoelen plaatsnam was dat een voor U ongecompliceerde gebeurtenis. U ziet een stoel, weet dat U op zoiets kunt plaats nemen en vervolgens doet U dat ook. In Uw hersenen is er een hersenspinsel op grond waarvan U deze actie snel en vol vertrouwen onderneemt. Zulke hersenspinselen zijn zeer belangrijk. U kunt niet zonder. Ik moet er niet aan denken dat ik eerst zou moeten nadenken over het soort materiaal waarvan de stoel vervaardigd is, of hij wel stevig genoeg zal zijn, enzovoorts. Met zo'n hersenspinsel gaat niet alles noodzakelijkerwijs feilloos: zo nu en dan zakken er mensen door stoelen. Hersenspinsels zijn talrijk en vaak ligt er enige wiskunde aan ten grondslag. Met wiskunde kun je er voor zorgen dat stoelen zo vervaardigd worden dat de kans op calamiteiten verwaarloosbaar klein is.
Bij andere voortbrengselen van de techniek is de rol van de wiskunde nog veel sterker aanwezig. Denk aan radio's, televisietoestellen, vliegtuigen, raketten, compact discs, computers. Veel te veel om op te noemen. Bij al dit soort apparaten heeft U zo Uw eigen hersenspinsels. Een compact-discspeler is een apparaat dat een duidelijk doel dient. Het is een doos met knoppen. Je kunt er een compact disc in stoppen. Als je op de juiste knoppen drukt dan gebeurt er meestal wel wat je ervan verwacht. Er komt muziek uit. Er is een ongelooflijke hoeveelheid kennis in zo'n apparaat verwerkt: kennis uit de natuurkunde, de informatica, de techniek, kortom kennis van al die vakken waarvan je iets zou leren als je de goede raad ``kies exact'' zou opvolgen. Bij al deze vakken speelt wiskunde op een of andere manier een rol en zelfs een cruciale rol.
Nu denkt U misschien dat ik nu ga zeggen dat wiskunde dus belangrijk is en dat daarom iedereen de wiskunde moet gaan bestuderen. Vervolgens beëindig ik deze rede en kunnen we na die gewichtige constatering snel aan de receptie beginnen. Ik wil het echter in een ander perspectief plaatsen.
Om een compact-discspeler te gebruiken hoef je geen wiskunde te kennen. Je kunt volstaan met een eenvoudig hersenspinsel. Daarvoor is zo'n apparaat een black box met enkele knoppen ter bediening ervan. Knappe koppen hebben het bedacht en U kunt het gebruiken en hoeft U niet te verdiepen in zulke duffe zaken als wiskunde. Dat is leuk voor nerds. Natuurlijk is het belangrijk en het is ook goed dat er mensen zijn die zich ermee bezig houden, maar dergelijk geestdodend werk kan ook door mensen uit andere landen gedaan worden. De immigratie uit de landen van het voormalige Oostblok begint trouwens al aardig op gang te komen.
Ook in de natuurwetenschappen bedient men zich van hersenspinsels. De bewegingswetten van Newton zijn vervat in formules, wiskunde dus. Het gaat hier om een stukje wiskunde waarmee we de werkelijkheid beschrijven en in dit geval zelfs op een verrassend goede wijze. Het is een hersenspinsel op grond waarvan we met succes uitspraken doen over de werkelijkheid. We beschrijven de voor ons vaak wat mistige realiteit met iets dat ongewoon helder is, met iets waarover wij exact kunnen redeneren.
Alleen binnen de wiskunde kan exact geredeneerd worden. Daar hebben we de wiskunde nu juist voor. De mogelijkheid om exact te redeneren heeft ook een prijs: wiskunde is abstract, het is geen realiteit. Het is een krachtig hulpmiddel, maar het is ook niet meer dan een hersenspinsel.
Wiskunde is een wetenschap. Wetenschappen gaan ergens over, zij hebben een object van studie. Wiskunde gaat over abstracte zaken. Bijvoorbeeld over getallen, zoals de natuurlijke getallen: 0,1,2,3, enz. Een getal is abstract. Je komt in de natuur geen getallen tegen. Wiskunde is geen natuurwetenschap. Abstracte zaken zijn door de mens zelf bedacht en deze bedenksels zijn op hun beurt weer object van studie geworden. Abstract is overigens niet hetzelfde als moeilijk: een kind weet wat een getal is.
Laten we voor de duidelijkheid even bij de natuurlijke getallen blijven. Hoewel ze abstract zijn kunnen ze wel eigenschappen hebben: ze kunnen even zijn of oneven, ze kunnen een priemgetal zijn of juist samengesteld. Een extra complicerende factor is dat er zo veel zijn: er zijn er oneindig veel. Zoiets kom je in de natuur ook niet tegen. Als je de natuurlijke getallen gaat opsommen dan kom je nooit klaar, want er is altijd weer een volgend getal dat je nog niet hebt gehad. Ook dat weet een kind.
Niet alleen getallen zijn bedenksels van de menselijke geest. Ook meetkundige objecten als punten, lijnen en cirkels zijn dat. Die lijken wel op wat je in de natuur tegenkomt, maar in de wiskunde zijn het geheel abstracte zaken.
Pythagoras
Een zeer oude wiskundige stelling:
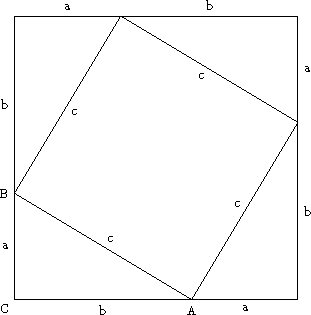
De Stelling van Pythagoras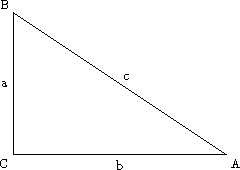 In een rechthoekige driehoek is het kwadraat van de hypothenusa gelijk aan de som van de kwadraten van de rechthoekszijden. |
Er zijn vele bewijzen voor deze stelling. Het volgende bewijs is gemakkelijk te onthouden.
Bewijs van de Stelling van Pythagoras
Het grote vierkant heeft zijden a+b en dus een oppervlakte
De vier rechthoekige driehoeken hebben elk een oppervlakte ½ab en dus
ofwel
Om in te zien dat de figuur met zijden c een vierkant is kan de stelling worden gebruikt die zegt dat de som van de hoeken van een driehoek 180° is. |
Er zijn oneindig veel rechthoekige driehoeken. Toch is het hiermee voor al deze driehoeken bewezen. Het is een soort gedachtenexperiment: je voert deze constructie uit op een willekeurige rechthoekige driehoek, d.w.z. een driehoek waarvan je verder alleen maar weet dat hij rechthoekig is. Meer mag je in het bewijs dan ook niet gebruiken. Verder mag je natuurlijk al wel conclusies trekken op grond van al eerder bewezen stellingen. Het bewijs brengt de te bewijzen uitspraak terug tot uitspraken die we al als waar hebben geaccepteerd, zoals hier bijvoorbeeld de stelling dat de som van de hoeken van een driehoek 180° is. Dit alles hangt samen met de axiomatische methode in de wiskunde. Deze stamt uit de Griekse oudheid en is van grote invloed geweest op de ontwikkeling van het vak.
De Stelling van Pythagoras is geen natuurwet. Dan zou het de Wet van Pythagoras zijn. Hij zou dan zijn gevonden door een aantal rechthoekige driehoeken te tekenen, daarvan de zijden te meten, de gemeten lengten te kwadrateren en te constateren dat de som van twee van deze getallen dicht bij het derde getal ligt. Afwijkingen zijn dan toe te schrijven aan meetfouten.
Euclides
Nog een stelling uit de Griekse oudheid: een stelling van Euclides.
Een Stelling van Euclides√2 is een irrationaal getal |
Een bewijs ervan berust op:
Hulpstelling
Ieder positief geheel getal n is op unieke wijze een product van een macht van 2 en een oneven getal.D.w.z. er zijn unieke natuurlijke getallen m en k zo dat |
Ook hiervan wordt het bewijs geleverd door voor een willekeurig getal de waarheid aan te tonen: dit is een wiskundige stelling en geen natuurwet. De genoemde stelling van Euclides volgt eenvoudig.
Bewijs van Stelling van Euclides
Het bewijs gaat uit het `ongerijmde': De exponent van 2 is wegens de Hulpstelling uniek. Eenzelfde getal kan niet zoals hier zowel oneven als even zijn. Tegenspraak! Er zijn dus niet zulke getallen a en b. |
Deze stelling is zelfs moeilijk als natuurwet te interpreteren. √2 is volgens de stelling van Pythagoras de lengte van de schuine zijde van een rechthoekige driehoek met rechthoekszijden van lengte 1. Maar met een liniaal is de irrationaliteit niet te constateren.
√2 als lengte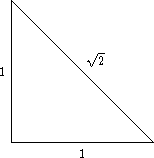
Pythagoras: 12 + 12 = (√2)2.
|
De wiskundige wereld is een abstracte wereld. Het is een abstracte wereld waar de een beter de weg weet dan de ander. Zij die er vaak in vertoeven weten dat het een wereld van een grote schoonheid is en dat er nog heel veel in te ontdekken valt. Wiskundig onderzoek heet dat.
Van eenvoud tot complexiteit
Bij sommigen leeft het misverstand dat de wiskunde, omdat het om een door de mens bedachte wereld gaat en men alleen logisch redeneren toelaat, een aanschakeling is van tautologieën en dus niet interessant kan wezen. Dat alles kan men rustig denken, als men er maar niet de conclusie uit trekt dat het daarom allemaal gemakkelijk is.
In de natuurwetenschappen komt men steeds meer tot inzichten die zijn samen te vatten als: eenvoud kan leiden tot complexiteit. DNA-moleculen bevatten blauwdrukken voor gecompliceerde organismen. Vele natuurverschijnselen hebben de structuur van een fractal: een wiskundig object met een heel eenvoudig constructie-principe en een zeer gecompliceerde structuur. De natuurlijke getallen 0,1,2,3,4 etc. vormen een eenvoudige structuur. Het gaat om een heel simpel hersenspinsel. Je kunt je er eenvoudige vragen over stellen. Soms duurt het eeuwen voor er een antwoord op dergelijke vragen wordt gevonden. Denk daarbij aan de laatste stelling van Fermat, een eeuwenoud probleem dat pas onlangs is opgelost door de Engelse wiskundige Andrew Wiles. Het is een resultaat van een eeuwenlang voortschrijdende verdieping van onze inzichten. De inzichten zijn inmiddels zo diep dat ze voor slechts weinigen nog toegankelijk zijn.
Een aansprekend voorbeeld van een complexe structuur die op een eenvoudig constructie-principe is gebaseerd is de Mandelbrot-verzameling. De constructie is als volgt:
Constructie van de Mandelbrot-verzameling
Bij ieder paar (a,b) van reële getallen is een rij (x,0, y0), (x,1, y1), (x,2, y2), ⋯ van zulke paren gedefinieerd door
Bij ieder punt (a,b) van het vlak hebben we zo een rij punten in het vlak. De Mandelbrot-verzameling bestaat uit die punten (a,b) waarvoor de bijbehorende rij niet `naar oneindig wegloopt.'
Met complexe getallen zijn deze rijen nog eenvoudiger te beschrijven.
|
Het resultaat staat hieronder en ook het resultaat van herhaald inzoomen met een factor van ongeveer 10.


Heel deze structuur ligt besloten in de zogeheten reële getallen. Dat zijn de getallen die je mooi kunt laten corresponderen met de punten op een rechte lijn, in schoolboeken soms kommagetallen genoemd. Het duurde tot in de negentiende eeuw voor men hier tot de juiste inzichten kwam. Vooral een goed idee van het begrip limiet is daarbij onontbeerlijk.
De Mandelbrot-verzameling heeft een eenvoudig constructie-principe. Wat hem interessant maakt is een wiskundige interpretatie die we hier met het oog op de tijd niet uit de doeken zullen doen. Ik wil alleen maar zeggen dat het hier niet om zuiver Spielerei gaat. De Mandelbrot-verzameling is pas in de belangstelling gekomen toen Mandelbrot met gebruikmaking van de nieuwe vinding van de computer hem zichtbaar wilde maken. De opkomst van het rekentuig heeft hier een grote rol gespeeld.