KORTE BESCHRIJVING

EENER


TRITMETISCHE LIJN,

BENEVENS

DERZELVER TOEPASSING

OP

DE VERDEELING VAN EENEN HOEK

IN

DRIE GELIJKE DEELEN.

door

P.J. BAUDET.



Te DEVENTER, bij
J. DE LANGE.
1834.




Aanvullende gegevens:
Oorspronkelijk tractaat 15 pp. met III uitklapbare figuren
Uitgegeven door J. de Lange: Deventer (1834).
Begin tekst op p. 5, de beide pagina's van het voorberigt zijn niet genummerd.
De opmaak van de formules is niet behouden waar het de delingen betrof; voor het wortelteken is \/ gebruikt. De vergeten verwijzing naar figuur 2 is tussen rechte haken op de daartoe geëigende plek ingevoegd.


VOORBERIGT.



Het vermaarde werkstuk van de verdeeling des hoeks in drie gelijke deelen is, op verschillende wijzen, door middel van kromme lijnen, inzonderheid door de toepassing der hijperbool, opgelost; doch de hier voorgesteld Tritmetische lost het werkstuk eenvoudiger op, en is daarenboven gemakkelijk te beschrijven. Er is, wel is waar, geen groot belang bij eene oplossing die niet regtstreeks tot de elementaire meetkunst behoort; maar men kan dezelve onder de wiskundige aardigheden, gelijk de Cissoïs, Conchoïs en Quadratix rangschikken, waarin toch een beminnaar der wiskunst eenige bespiegelingen vinden kan. De ijverige nalezer versmaadt zelfs de geringste korenaar niet.

De Schrijver.

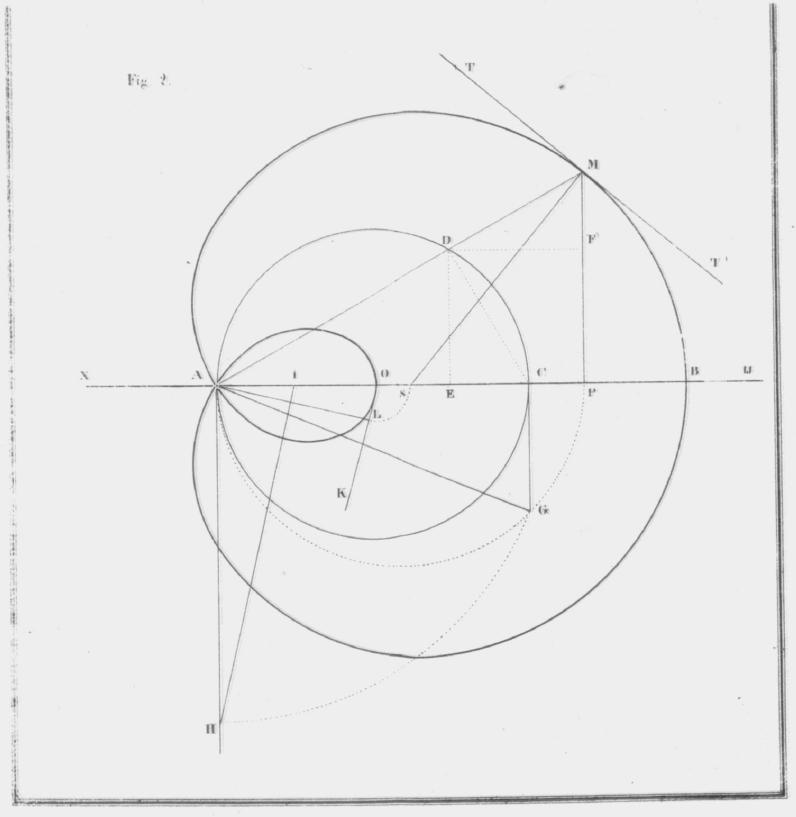
VAASSEN den 14 April 1834.



KORTE BESCHRIJVING

 EENER

TRITMETISCHE LIJN



§ I. De Tritmetische lijn door punten te beschrijven.

1. Door een willekeurig punt A, van den omtrek eens cirkels, trek een aantal lijnen. (Fig. 1.)
2. Neem op deze lijnen PM, P'M', P''M'', enz. gelijk aan den straal des cirkels.
3. Trek door de punten M, M', M'', enz. eene lijn: dezelve zal de Tritmetische zijn.
4. Neemt men Pm, P'm', P''m'', enz. gelijk aan den straal des cirkels, dan is mm'm'' eene tweede tak der Tritmetische lijn (a).
§ II. Over de Abscissen en Ordinaten der
Tritmetische lijn.

1. Onder het getal der lijnen, die men door A trekken kan, is ook AC, of de middellijn des cirkels, begrepen. Verlengt men dezelve in XY, dan kan XY gevoegelijk als as de abscissen genomen worden; terwijl [pag. 6] ZV, in het punt A loodregt op XY, de as der ordinaten zal zijn.
2. Zij r = de straal des cirkels, dan volgt uit de Constructie der Tritmetische
AN = PM = BC = r, alsmede,

An = Pm = OA = OC = r.

§ III. Over de vergelijking der Tritmetische lijn.

1. Om de vergelijking der Tritmetische lijn te bepalen, trek uit een punt M, naar welgevallen op de kromme lijn genomen, de Ordinaat MP loodregt op XY. (Fig. 2.)
2. Trek AM, DC, en voorts DE loodregt op XY, alsmede DF loodregt op MP.
3. Zij AE = z, AP = x, PM = y, dan is AC = 2r, DM = r, PE = x-z en CE = 2r-z.
4. In de gelijkvormige driehoeken ACD en DMF is
DM : DF = AC : AD.
of r : x-z = 2r : AD.
Zoo is AD = 2x - 2z
en AM = 2x - 2z + r.

5. In de gelijkvormige driehoeken AED en DFM is
AE : AD = DF : DM.

of z : 2(x-z) = x-z : r
Waaruit z = x + ¼r ± ¼\/(8rx + r²).

en 2z = 2x + ½r ± ½ \/(8rx + r²).

[pag. 7]
6. In den regthoekigen driehoek APM is
PM² = AM² - AP²

of y² = (2x - 2z + r)² - x²
De waarde van 2z, onder N° 5 gevonden, hierin substituerende, vindt men voor de vergelijking der Tritmetische lijn:

y² = [½r ± ½\/(8rx + r²)]² - x².

§ IV. Beschouwingen uit de vergelijking afgeleid.

1. De gevondene vergelijking, ofschoon schijnbaar van de tweede, is van de vierde magt; dewijl x onder invloed van het wortelteeken staat.
2. Er zijn dus vier waarden van y, namelijk:

a. y = + \/([½r + ½\/(8rx + r²]² - x²).

b. y = - \/([½r + ½\/(8rx + r²]² - x²).

c. y = + \/([½r - ½\/(8rx + r²]² - x²).

d. y = - \/([½r - ½\/(8rx + r²]² - x²).

3. De ordinaten a en b, alsmede c en d zijn dus twee aan twee aan elkander gelijk, met het eenige verschil van + en -; zoodat de Tritmetische lijn aan beide kanten van de as der abscissen volkomen dezelfde gedaante heeft.
4. Stelt men in de vergelijking x = 0, dan vindt men voor a en b
y = ± r.
Hetgene reeds § II.2 opgemerkt is.
De vergelijkingen c en d geven
y = 0.
waaruit blijkt dat er in A slechts twee ordinaten bestaan. [pag. 8]
5. Stelt men x = r, dan vindt men:

Voor a en b, y = r\/3

Voor c en d, y = 0.

Waaruit blijkt dat de Tritmetische in het punt O slechts twee ordinaten heeft, terwijl de twee overige, gelijk in het vorige geval in 0 overgaan.
6. Stelt men x > r, of x = r + d, dan is voor c en d:
y = ± \/[-½r² - d² - ½\/(9r² + 8dr)]

Deze twee ordinaten zijn dus alsdan onbestaanbaar, zoodat de tak m''m''' zich niet verder dan het punt O uitstrekt.
7. Stelt men x = 2r, dan vindt men voor a en b:
y = ± ½r\/(2 + \/17).

8. Stelt men x = 3r, dan vindt voor a en b:
y = 0.

Waaruit blijkt dat de groote takken der Tritmetische in het punt B zamenloopen; terwijl men y onbestaanbaar zal vinden, wanneer men x = 3r + d stelt.
9. Aan den negatieven kant der abscissen, zal men den gang der coördinaten spoedig ontdekken, door x negatief in \/(8rx + r²) te nemen. Men verkrijgt alsdan:
\/(r² - 8rx).

Deze uitdrukking wordt 0, wanneer 8rx = r², of x = r/8 wordt, in welk geval men voor de ordinaten zal vinden:
y = ± \/[(½r)² - r²/64] = 1/8r\/15.

10. Stelt men x = - (1/8r + d), dan is

\/(8rx + r²) = \/(r² - r² - 8dr) = \/-8dr.

[pag. 9] Waaruit blijkt dat de ordinaat alsdan onbestaanbaar is. Zoodat men voor de grootste negatieve waarde x = r/8 vindt.
§ V. Den stand der grootste Ordinaat, en de Subnormaal
der Tritmetische lijn te bepalen.

1. De formule, § III gevonden, kan geschreven worden:
y² = ½r² + 2rx - x² ± ½r\/(8rx + r²).

Dezelve differencierende, heeft men:
2ydy = 2rdx - 2xdx ± 2r²(8rx + r²)-½dx.

Dewijl nu de Subnormaal algemeen voorgesteld wordt door ydy/dx, zoo vindt men:
Subn. = r - x ± r²/(\/8rx + r²)

2. Daar de stand der grootste Ordinaat met Subnormaal = 0 overeenkomt, zoo vindt men de abscisse van dat punt, door de volgende vergelijking op te lossen, namelijk:
r - x ± r²/(8rx + r²) = 0.

Waaruit x = r·(15 ± \/33)/16

3. De gevondene waarde der Subnormaal is zeer eenvoudig en gemakkelijk te construeren.
Stelt men r²/(8rx + r²) = v. [pag. 10]

Teller en noemet van het eerste lid door 2 deelende vindt men:
v = ½r²/(2rx + ¼r²)

Om v te construeren [Fig. 2],
1. Beschrijf opAP eenen halven cirkel.
2. Trek CG loodregt op AP en trek AG, dan is:
AG² = AC × AP = 2rx.
3. Breng AG in AH loodregt op AP over.
4. Deel AO in 2 gelijke deelen in I, en trek IH, dan is: IH = \/(2rx + ¼r²).
5. Trek OK evenwijdig aan IH en AL loodregt op OK, dan is, in de gelijkvormige driehoeken AOL en AIH,
IH : AI = AO : OL

of \/(2rx + ¼r²) : ½r = r : OL

Waaruit OL = ½r²/[\/(2rx + ¼r²)]

Dewijl de Subnormaal van den voet der Ordinaat af gerekend wordt, is PO = r - x.
Breng dus OL in OS over, slechts de positieve waarde nemende, dan is:
PS = r - x + r²/[\/(8rx + r²)]

Dewijl het teeken +, bij den derden term, tot den tak MM' behoort, zal men eene Tangens tot de Tritmetische lijn kunnen trekken; door eerst de Normaal SM, en voorts TT' door het punt M loodregt op SM te trekken. [pag. 11]
§ VI. Werkstuk. Door middel der Tritmetische lijn
eenen gegevenen hoek in drie gelijke deelen te
verdeelen.

Oplossing. Fig. 3

1. Zij O het middelpunt des cirkels, die tot het beschrijven der Tritmetische gediend heeft, en AB deszelfs verlengde middellijn.
2. Breng den top des gegevenen hoeks in O, en laat een van deszelfs beenen langs OB vallen; terwijl het andere de Tritmetische ergens in F ontmoet.
3. Trek AF, dan is:
/ AFO = 1/3 / FOB.

Bewijs.

Trek OF', dan is AO = OF' = FF'.
/ AFO = / FOF' = a.
/ AF'O = / AFO + / FOF' = 2a.
/ FAO = / AF'O = 2a.
/ FAO + / AFO = / FOB.
of 2a + a = / FOB.
3a = / FOB.
a = 1/3 / FOB.

§ VII. Gevolgen van het voorgaande werkstuk.

1. De lijn AF snijdt de tweede tak der Tritmetische ergens in f. Trekt men PQ door O en f, dan is PQ loodregt op OF. [pag. 12]
Bewijs.
OF' = fF' = r
dus is /fOF' = /OfF'.
en /fOF' + ½b = |
Maar ½b = a = /FOF'.
Dus is /fOF' = /FOF' = | .
en PQ loodregt op OF.
2. Trekt men AQ, dan is
/ AQO = a + 1/3.

Bewijs.
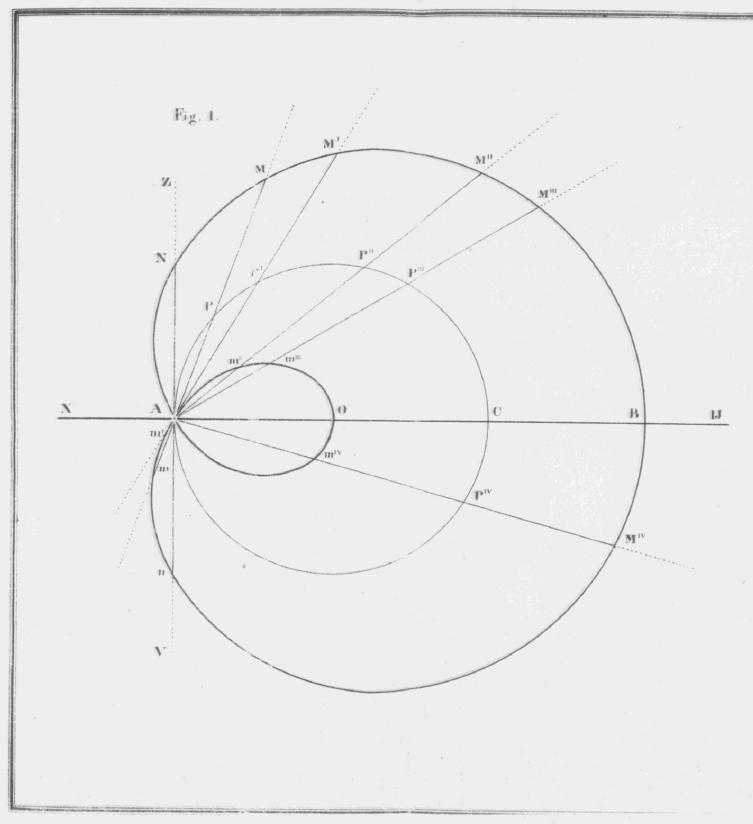
/ AQO = 1/3/ QOB. § VI.
/ AQO = 1/3/ (3a + | ).
/ AQO = a + 1/3| .
3. Trekt men AP, dan is:
/ APO = 1/3| - a.

Bewijs.
/ APO = 1/3/ POB. § VI.
= 1/3 (| - / FOB).
= 1/3 (| - 3a).
a' = 1/3 | - a.
4. De som der hoeken AFO en APO is bestendig = 1/3 | .
Bewijs.

a' = 1/3 | - a. 3de Gevolg.
Dus is a + a' = 1/3 | .

[pag. 13]

5. De hoek FAP is bestendig = 2/3 | .
Bewijs.

/c = / FOB - a = 2a.
/c' = / POB - a' = 2a'.
Dus is / FAP = 2(a + a') = 2/3 | .
6. Verlengt men FO tot R, dan snijdt zij AP ergens in de Tritmetische, in p.
Bewijs.

OP' = PP'
dus is / POP' = / OPP'
/pOP' + / OPP'= | .
of / pOP' + a' = | .
en / OpP' + / OPp = | .
of / OpP' + a' = | .
Derhalve is / pOP' = / OpP'.
en OP' = pP'.
Dus is het punt p aan de Tritmetische.
7. Trekt men AR, dan is:
/ ARO = a' + 1/3 | . 2de Gevolg.
8. QAR is eene regte lijn.
Bewijs.
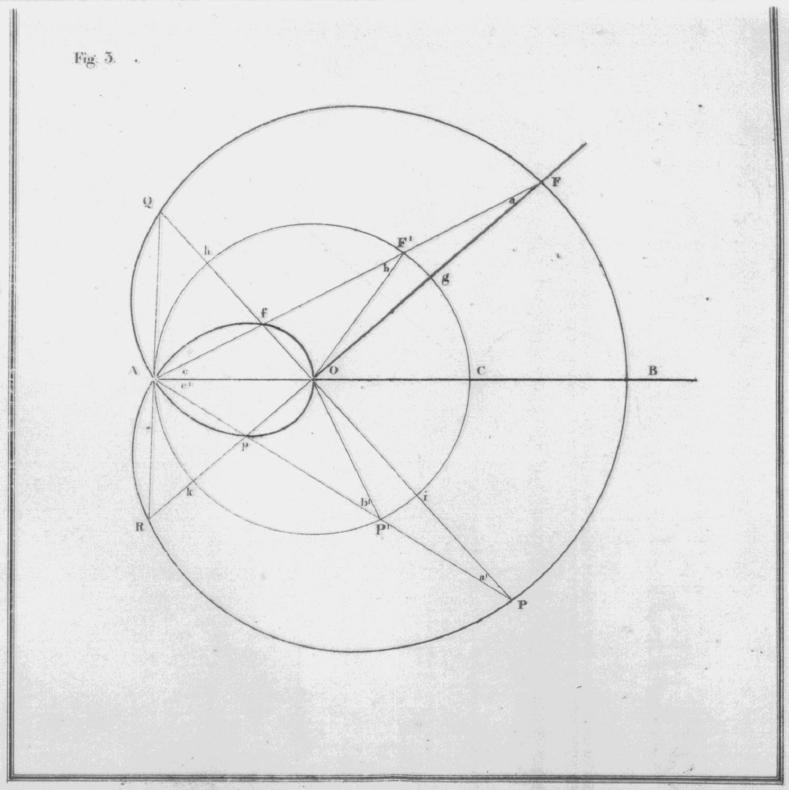
/ BAQ = 2| - /AQO - / AOQ.
= 2| - a -1/3| - 3a'.
/ BAR = 2| - / ARO - / AOP.
= 2| - a' - 1/3| -3a.

[pag. 14]

/ BAQ + / BAR = 4 | - 4a - 4a' - 2/3| .
Maar 4a + 4a' = 4/3| .
Dus is / BAQ + / BAR = 2 | .
en QAR eene regte lijn.
9. De hoek FAQ is bestendig = 2/3| .
Bewijs.
/ BAQ = 2| - 1/3| - a - 3a'
en / BAF = 2a
Zoo is / FAQ = 2| - 1/3| - 3(a+a') = 2/3| .
Insgelijks is / PAQ = 2/3| .
10. Stelt men zich voor dat het punt F zich naar Q beweegt, dan beweegt zich tevens P naar F. De lijn FF'fA gaat in QAR over, terwijl / APQ eerst in B tot nul overgaat, en dus in F als negatief moet beschouwd worden. Hierin is de algemeenheid van het 4de gevolg opgesloten.
Of / AQO - / AFO = 1/3| .
11. Niet alleen scherpe en stompe hoeken, maar ook grootere cirkelruimten dan 2| worden door de Tritmetische lijn in drie gelijke deelen verdeeld.
Want / fOF' = 1/3 CP'Ah.
Bewijs.
gP'Ah = 3 | .
Cg = 3a.
[pag. 15] CP'Ah = 3 | - 3a.
en / fOF' = | - a.
Zoo is /fOF' = 1/3 CP'Ah.
Insgelijks is /pOP' = 1/3 CF'Ak.
Men vindt voorts /AfO = 1/3 CF'Ai.
en / ApO = 1/3 CP'Ag.
12. De Tritmetische lijn, niet van den gegevenen hoek afhankelijk zijnde, kan voor de driesnijding van alle hoeken dienen.




Voetnoot:

(a) Men kan des verkiezende, de Toepassing, bij § VI voorgedragen, hierop laten volgen.