|
| in KANT'S Transcendentale Aesthetiek:
| in RUSSELL'S Foundations of Geometry:
| in dit werk
|
| Onafscheidelijk gebonden aan de uitwendige ervaring:
| de Euclidische driedimensionale ruimte, en de maatlooze tijd.
| de Euclidische driedimensionale ruimte, en de meetbare
tijd-coördinaat.
| niets.
|
| Noodzakelijk treedt op in het wiskundig receptaculum der ervaring:
|
|
|
|
| a) op grond van de organisatie van het menschelijk intellect:
| de Euclidische driedimensionale ruimte, en de maatlooze tijd.
| de projectieve ruimte, de vrije bewegelijkheid in de ruimte, en de
meetbare
tijd-coördinaat.
| de oer-intuitie der wiskunde, of tijdsintuitie.
|
| b) op grond der ervaring:
| niets
| de driedimensionaliteit der ruimte en het parallellenaxioma van
EUCLIDES.
| niets.
|
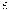 /\(xa)
het maximum der spelingsgebieden tusschen xa en
xa + /\ van
de verschillende differentiequotienten, zooals die
hooren bij de verschillende aangroeiingen der onafhankelijke
veranderlijke xa, wanneer men die aangroeiingen
achtereenvolgens alle waarden laat doorlopen
tusschen 0 en een zekere zoo klein als men wil, doch
vast te kiezen waarde a, dan volgt uit het zooeven
genoemde postulaat, dat
/\(xa)
het maximum der spelingsgebieden tusschen xa en
xa + /\ van
de verschillende differentiequotienten, zooals die
hooren bij de verschillende aangroeiingen der onafhankelijke
veranderlijke xa, wanneer men die aangroeiingen
achtereenvolgens alle waarden laat doorlopen
tusschen 0 en een zekere zoo klein als men wil, doch
vast te kiezen waarde a, dan volgt uit het zooeven
genoemde postulaat, dat
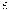 /\ met /\ tot 0 nadert.
Verder hebben we, onder p/n een echte
breuk verstaande:
/\ met /\ tot 0 nadert.
Verder hebben we, onder p/n een echte
breuk verstaande: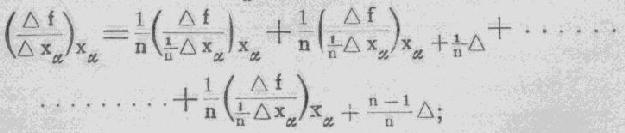
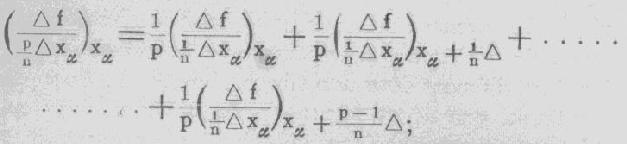
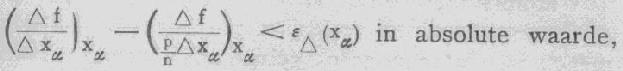
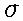 /\(xa)
der differentiequotienten voor aangroeiingen van xa,
gelijk aan een echte breuk maal /\, kleiner is dan
2
/\(xa)
der differentiequotienten voor aangroeiingen van xa,
gelijk aan een echte breuk maal /\, kleiner is dan
2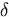 , dan
nemen de spelingsgebieden
, dan
nemen de spelingsgebieden
 ,
,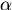 sin
sin