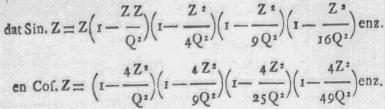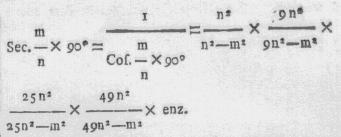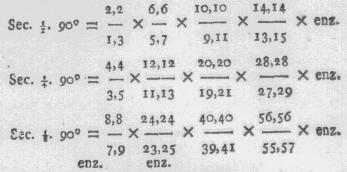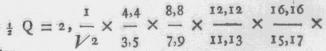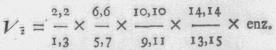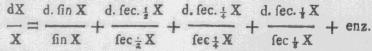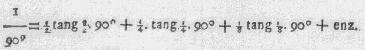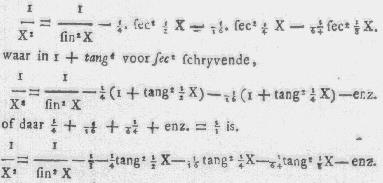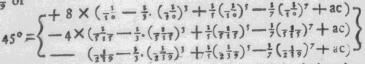Betoog
van eene
merkwaardige eigenschap des Cirkels,
waar door men deszelfs omtrek tot den uitersten trap van naauwkeurigheid
meetkunstig kan construeeren; door
JACOB de GELDER
Leermeester in de Wiskunst, te Rotterdam
Aanvullende gegevens:
Oorspronkelijke artikel in: Nieuwe Algemene Konst- en Letterbode
VI nr. 153 (vrijdag 2 December 1796), pp. 177-181.
Tweekoloms opmaak, met voetnoot en platen in de tekst.
Opmaak van de formules in de tekst niet behouden, uitgezonderd de formules
die in plaatvorm zijn opgenomen.
Het zou byna eene lompe onkunde in iemand onderstellen,
indien hy, op het voetspoor van veele vergeefsche zoekers, in staat meende te
zyn, om den Quadratuur van den Cirkel te kunnen bepaalen; zo veele ervaren
Wiskundigen hebben dit werk vruchteloos ondernomen, en de verschillende wegen,
die men is ingeslagen, hebben even zoveele bewyzen van de onmogelykheid deezer
onderneeming aan de hand gegeeven. Men heeft uitdrukkingen in reeksen en
geduurige producten gevonden, die wel is waar den omtrek van den Cirkel juist
uitdrukken; maar daar deeze reeksen of producten door geen getal ooit bepaald
zyn geworden, heeft men zeer waarschynlyk ondersteld, dat de middellyn tot den
omtrek eene onmeetbaare grootheid is, dat is te zeggen: dat geen evenmatig deel
van de middellyn een evenmatig deel van den omtrek kan worden. Daar nu in de
Meetkunst verscheidene onmeetbare grootheden, als by voorbeeld de diagonaal van
een vierkant en meer andere geconstrueerd kunnen worden, kan men natuurlyk
vraagen: of het ook insgelyks niet mogelyk zou zyn, om eene regte lyn te
construeeren, die volmaakt aan den omtrek des cirkels gelyk ware? Verscheide
geleerden hebben daar aan getwyffeld, en voor zo verre my bewust is, heeft
niemand de onmogelykheid daar van aangetoond.
De eigenschap van den cirkel, die ik hier ter plaatse zal
mededeelen, en de constructie, die ik 'er uit zal afleiden, schynen niet veel
hoop voor deeze vinding overtelaaten, en bewyzen ten minsten, dat men ten
opzichte van de constructie aan gelykzoortige zwarigheden gebonden is, als
welke zich by de berekening in getallen opdoen.
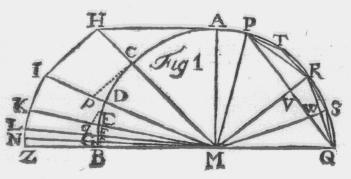
Laat (Fig. 1.) PMQ een cirkel-sector verbeelden, welke door
de radien RM, SM, enz. in twee, vier, agt, enz. deelen verdeeld zyn. Indien men
dan de chorden PQ, PR en RQ trekt, zyn de driehoeken MRW en QVR gelykvormig, en
dienvolgens is MW tot RM gelyk QV tot QR; stellende nu de Radius des cirkels
=1, de boog PQ = X, is de proportie Cos (X/4) : 1 = (Chorde X)/2 : Chorde
(X/2), waar uit men haalt, 2. Chorde (X/2) = Chorde X × Secans van X/4;
deeze uitdrukking geeft ons deeze eigenschap, dat: ,,tweemaal de chorde van de
helft van eenigen boog verkreegen word, indien men de chorde van dien boog met
de secans van een vierde deezes boogs vermenigvuldigt.'' Het is dus zeer klaar,
dat men de boogen QR en PQ elk wederom in twee deelen verdeelende, en elk
deezer deelen wederom in twee deelen, dezelfde eigenschap op elke term van de
reeks deezer deelen zal toepasselyk zyn, en dat men door substitutie van de
waarde van elke voorgaande term in den volgenden, de onderstaande tafel zal
kunnen formeeren.
2 chorde (X/2) = chorde X × sec (X/4)
4 chorde (X/4) = chorde X × sec (X/4) × sec (X/8)
8 chorde (X/8) = chorde X × sec (X/4) × sec (X/8)
× sec (X/16)
16 chorde (X/16) = chorde X × sec (X/4) × sec (X/8)
× sec (X/16) × sec (X/32)
Indien men nu opmerkt, dat 2 chorde (X/2) = PR × QR; 4 chorde
(X/4) = QS×SR×RT×PT enz., ziet men klaar, dat men, hoe verder men de
bovenstaande vergelykingen voordzet, men des te nader zal komen aan de waarde
van den boog X, welke de limiet is van den benedensten omtrek der veelhoekige
figuuren die door de chorden der verdeelde boogen gemaakt worden. Hier uit kan
men afleiden, dat, daar men nooit tot de laatste term kan komen, hoe verre ook
de verdeeling mogte voordgezet worden, de lengte van den boog aldus zal
uitgedrukt worden
X = chorde X × sec (X/4) × sec (X/8) ×
× sec (X/16) × sec (X/32) enz.
moetende de termen van dit geduurig product zo lang voordgezet worden, tot dat
men door de geduurige verdeeling der boogen tot een boog komt, die = 0 is, en
dus geene verdere verdeeling kan toelaaten, hetgeen nooit kunnende gebeuren,
een genoegzaam bewys is, dat ook deeze formula de waarde van den boog slechts
by benadering kan doen bekend worden.
Dewyl de chorde van X = 2 sin (X/2) =
= (sin X)/(cos (X/2)) =
= sin X . sec (X/2),
verkrygt men de bovenstaande waarde onder deeze gedaante,
(A) X = sin X × sec (X/2) × sec (X/4) × sec (X/8) × enz.
En stellende X = 90°, zal man, dewyl de sinus van
90 graden = 1 is, voor de lengte van een boog van 90 graden deeze uitdrukking
verkrygen.
(B) boog van 90° = sec (90°/2) × sec (90°/4)
× sec (90°/8) × sec (90°/16) × enz.
Deeze laatste uitdrukking bevat een zonderlinge eigenschap
van den cirkel, die alhoewel zy van het voordeel eener gemaklyke berekening
geheel ontbloot is, echter de volgende merkwaardige constructie
oplevert.
Laat (Fig. 1.) ABM een
quadrant zyn: deel den boog AB in C in twee gelyke deelen, de helft BC in D; BD
in E, BE in F enz. elke helft telkens in twee gelyke deelen: trek wyders door
de deelpunten C, D, E de [pag. 179] onbepaalde snylynen MCH, MDI, MEK enz.,
indien men dan
eindelyk de loodlynen AH, HI, IK, KL, LN op AM, MH, MI enz. trekt, zal men
hebben:
MH = sec (90°/2)
MI = sec (90°/2) × sec (90°/4)
MK = sec (90°/2) × sec (90°/4) × sec
(90°/8)
ML = sec (90°/2) × sec (90°/4) × sec
(90°/8) × sec (90°/16) enz.
Want de lynen Cp en Dq loodrecht op CM en Dm trekkende, heeft
men in de gelykvormige driehoeken MHI en MCp deeze evenredigheid; CM : MH = Mp :
MI of 1 : sec (90°/2) = sec (90°/4) : MI derh. MI =
sec (90°/2) × sec (90°/4). -- en wederom zal men uit de
gelijkvormige driehoeken MIK en MDq bewyzen, dat MK = sec (90°/2) ×
sec (90°/4) × sec (90°/8) en op gelijke wijze met de
andere vergelykingen.
Indien men met deeze bewerking voordgaat, zal men eindelyk
tot eene zeer groote benadering komen: indien men in een cirkel van 100 voeten
radius de bewerking tot 12 of 13 maalen voordzet, zal de lyn die men eindelyk
verkrygt geen 100ste deel van een duim minder dan de lengte van het quadrant
zyn, en indien het mogelyk ware, om de verdeelingen tot in het oneindige te
agtervolgen, zou men ten laatsten tot de lyn MZ komen, welke aan de lengte van
het quadrant volmaakt zou gelyk zyn.
De zamenhang van de eigenschappen der grootheden is
verwonderlyk, en doet ons de volstrekte zekerheid der Wiskundige waarheden
overtuigend gevoelen, zo dikwyls wy dezelfde resultaaten uit verschillende
beginsels zien te voorschyn komen. Zo is het ook met de uitdrukking (B) gelegen, welke wy uit de gemeene beginselen
der meetkunst afgeleid hebben: doch indien men de radius = 1 een boog van
180° = Q, weeten wy
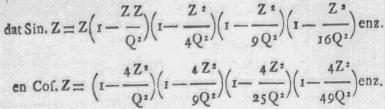
stellen wy in de eerste deezer reeksen Z = Q/2; dan is sin Z = 1 en
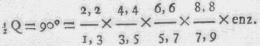
de bekende uitdrukking van WALLIS, en stellende in de tweede uitdrukking voor
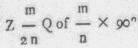
verkrygen wy
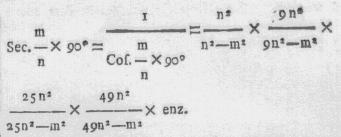
stellende nu in deeze laatste uitdrukking successivelyk voor m altijd 1, en
voor n, 1, 2, 3, 4 enz., zal men de volgende uitdrukkingen in getallen
verkrygen.
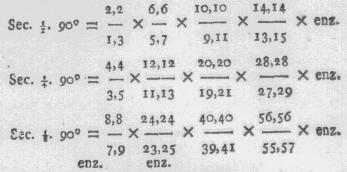
Indien men nu deeze vergelykingen met elkander
vermenigvuldigt, verkrygt men:

Indien men in de uitdrukking van sin. Z, Z = Q/4 stelt, zal
men
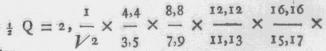
enz. vinden.
Waar uit men voor de [vierkantswortel] deeze uitdrukking
vindt:
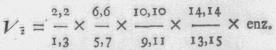
daar nu de [vierkantswortel] de chorde is, welke een boog van 90°
onderspant, ziet men dat de reden van de chorde van 90° tot den boog
van 90° is gelyk de eenheid tot de waarde van
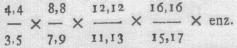
Indien het nu mogelyk ware, de waarde van het geduurig product
deezer breuken in eenige eindige, al ware het maar eene surdische uitdrukking
te vinden, zou de boog van 90° kunnen geconstrueerd [pag. 180]
worden. Maar
alle pogingen, die ik daar toe in het werk gesteld heb, zyn vruchteloos
afgeloopen; dan hoe het zy, dit oneindig product heeft eene rationaale of eene
irrationaale waarde, die ik a zal noemen, de boog van 90° zal =
a[wortel-2] zyn: indien nu a rationaal is, is de waarde van a[wortel-2]
onmeetbaar en zo a zelve onmeetbaar is kan a[wortel-2] niet meetbaar worden ten
zy a zelve van den vorm b[wortel-2] is; maar zulks ziet men op de enkele
beschouwing van de uitdrukking, met die van de waarde van [wortel-2]
vergeleken, dat niet mogelyk is; men kan dan veilig besluiten dat de radius tot
de lengte van een boog van 90° onmeetbaar is: en zou dus de
quadratuur van den cirkel in getallen te willen vinden niet hetzelfde zyn als
of men vinden wilde dat tweemaal twee iets meer of minder dan vier ware?
(*)
Men kan uit de reeks
(A), die ik boven
opgegeeven heb, nog veele andere merkwaardige reekzen afleiden, welke de
kortheid van mijn bestek my niet toelaat alhier te plaatsen: eene of twee die
zeer merkwaardig zyn, zal ik hier byvoegen, om dat deeze stof tot verdere
onderzoekingen kunnen opleeveren.
Indien men de uitdrukking
(A) in Logarithmen brengt, zal men hebben
log. X = log. sin X + log. sec (X/2) + log. sec (X/4) + log.
sec (X/8) + enz. waar van de differentiaal is,
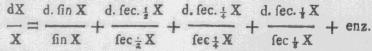
dewyl nu d. sec (X/2) = 1/2 tan (X/2) × sec (X/2) × dX en d. sin X = dX cos X is,
zal men deeze waarden in de differentiaal vergelyking overschryvende, en alles
door dX deelende, verkrygen
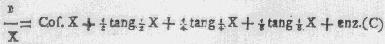
welke reeks, indien men X = 90° stelt, en in aanmerking neemt dat
cos 90° = 0 is, deeze onderstaande oplevert
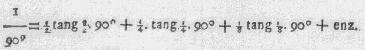
Indien men de reeks (C)
wederom differentieert, verkrygt men
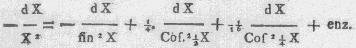
welke door dX gedeeld zynde, na de verschikking der termen geeft
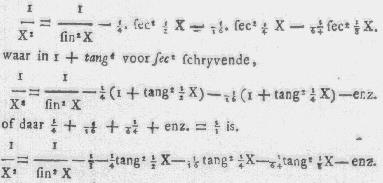
oplevert, en in welke voor X, 90° schryvende, en in aanmerking
neemende, dat sin 90° = 1 is, deeze reeks geeft
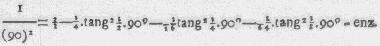
Men moet bekennen dat deeze reeksen voor de berekening
voorzeker de geschikste niet zyn, 'er zyn tot dat oogmerk andere handelwyzen,
die met meer gemak kunnen behandeld worden. EULER heeft in zyne Introd. ad
Anal. Infinit. Part I pag. 106 aangetoond, hoe men een boog van
45° in twee of meer boogen kan verdeelen, welker tangenten
rationaale getallen zyn, hoedanige zyn een boog, waar van de tangens 1/2 en die
waarvan de tang. 1/3 is, welke beide boogen te zaamen 45° uitmaaken,
en elk van welke door de reeks + - 1/3 + 3 + 1/5 + 5 - enz., die de waarde van
een boog uitdrukt wiens tangens + is, zeer gemaklyk kan berekend worden.
Eindelyk heeft volgends het getuigenis van HUTTON (zie zyne Treatise on
Mensuration pag. 120,121) MACHIN aangetoond, dat een boog van
45° gelyk is aan viermaal een boog, wiens tangens 1/5 is min een
boog wiens tang. 1/239 is; zo dat
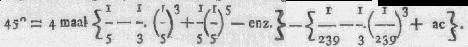
dit kan nog aanmerkelyk verkort worden; want dewyl uit de
formule tang 2p = (2 tang p)/(1 - tan² p) blykt, dat de tangens van
2 maal een boog wiens tangens 1/10 is = is aan (2/10)/(1 - 1/100) = 20/99 het
welk grooter is dan 1/5 en tang (p - q) = (tan p - tan q)/(1 + tan p . tan q) =
(20/99 - 1/5)/(1 + 4/99) = 1/515 is, zal men voor een boog van 45°
deeze uitdrukking hebben: 45° = [pag. 181] 8 maal. boog. tang.
(1/10) - 4 boog. tang. (1/515) - boog. tang. (1/239) of
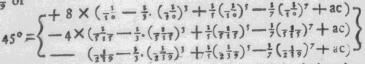
in welke uitdrukking het getal 10 veel gemak in de bereekening geeft.
Het zal by deeze gelegenheid niet te onpas komen, om de
nagedagtenis van onzen grooten NIEUWLAND by de Vaderlandsche leezers te
verëeren. Professor VAN SWINDEN zegt in de aantekeningen op de Lykrede van
NIEUWLAND in Felix Meritis uitgesproken, pag. 141, dat NIEUWLAND een
zeer eenvoudige Constructie van de proportie 113:355, door METIUS voor de reden
van den omtrek des cirkels opgegeeven, gevonden heeft. Ik heb dit leezende eene
dergelyke Constructie gevonden, indien NIEUWLAND niet by geval een figuur
ontdekt heeft, waar in eenige lynen die proportie opleveren, zal zyne
Constructie mogelyk hier op uitkomen:
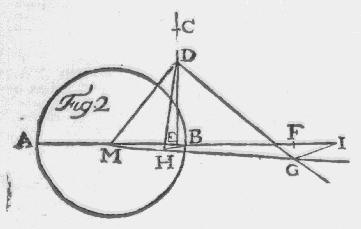
Dewyl 113 gelyk is aan de som van de quadraaten van 7 en 8 en
355 gelyk is aan tweemaal het vierkant van 11 plus 113, neem ik figuur 2, (AB
de middellyn en M het middelpunt van een cirkel zynde,) op een wel verdeelde
schaal waar van de deelen niet al te klein zyn, een lyn ME van 7 deelen, voords
ED gelyk aan 8 deelen en trek de lyn MD; eindelyk neem ik nog EC = EH = 11
deelen en DG loodrecht op MD getrokken hebbende, neem ik DG = CF en laat CH
loodrecht op MG vallen, en dan staat de lyn MH tot de lyn MG gelyk 113 tot
355.
Want MD² = ME² + ED² = 49 +
64 = 113, en DG² = CH² = 2 · 121 = 242; derhalven
MG² = MD² + DG² = 113 + 242 = 355; nu is MH :
MG = MD² : MG² = 113 : 355; indien men dus GI evenwydig
aan HB trekt, zal MI = den halven omtrek van een cirkel zyn.
Indien men door de geduurige breuken de reden van den omtrek
tot de middellyn des cirkels, door een reeks van eindige breuken benaderd, zo
als men zien kan in myne Grondbeginselen der Cyfferkunst, pag. 417, kan
men voor de volgende breuken ook diergelyke constructien vinden, die echter op
verre na zo eenvoudig niet zyn als deeze, en welke uit dien hoofde zo zeer niet
verdienen aangepreezen te worden, te meer, dewyl de constructie van METIUS, zo
naauwkeurig is, dat men vooronderstellende, dat de radius in tien millioen
deelen verdeeld is, deeze geconstrueerde omtrek geen 3 deelen van den waaren
omtrek verschilt, eene naauwkeurigheid, welke men zelfs, uit hoofde der
onnaauwkeurigheid, welke men zelfs, uit hoofde der onnaauwkeurigheden waar aan
de Meetkunstige constructien onderworpen zyn, niet eens verwagten kan, in
constructien, die theoretisch volkomen kunnen uitgevoerd worden.
Voetnoot
(*) VAN DER MONDE heeft in de Memoires de l'Acad. des Sciences de Paris
1772, I Partie pag. 489, aangetoond, dat de boog van 90° eene
irrationaale grootheid van eene hoger orde is.