Een sonderlinghe boeck in dye edel conste
Arithmetica
 Dat eerste deel vander Rekeninghe
Numeracie / oft
tellinghe.
Dat eerste deel vander Rekeninghe
Numeracie / oft
tellinghe.
Leert die wtsprekinghe der ghetalen.
Die eerste Reghele.
Daer zijn neghen bediedelicke figueren doer welcke men alle ghetal scrijft / als
.1.2.3.4.5.6.7.8.9. En de thiende is een onbediedelijcke als 0, nullio ghenaemt
/ de welcke voor haerselu
scrijft / als
.1.2.3.4.5.6.7.8.9. En de thiende is een onbediedelijcke als 0, nullio ghenaemt
/ de welcke voor haerselu niet en
bediet. Maer w
niet en
bediet. Maer w neer si wert
ghestelt voor die bediedelicke tegen die rechte
h
neer si wert
ghestelt voor die bediedelicke tegen die rechte
h t so bringet si
een yegelijcx ghetal bediedende thien werf also veel als in dese exempele, 24 is
vier en [fo.1. verso] twintich. Stelt een .0. daervoor
t so bringet si
een yegelijcx ghetal bediedende thien werf also veel als in dese exempele, 24 is
vier en [fo.1. verso] twintich. Stelt een .0. daervoor als .240. so hebt ghi
twee hon
als .240. so hebt ghi
twee hon t e
t e veertich. Ooc so veruult
si de lege plaetse / als oft ic wilde scriv
veertich. Ooc so veruult
si de lege plaetse / als oft ic wilde scriv duysentvijfhon
duysentvijfhon t e
t e twintich so settick voor
dit ghetal die onder thien sijn / welc daer gheen en is / een nulla e
twintich so settick voor
dit ghetal die onder thien sijn / welc daer gheen en is / een nulla e staet aldus .1520.
staet aldus .1520.
 Die tweede Reghele.
Die distinctie oft ordinancie der ghetalen beghint van
Die tweede Reghele.
Die distinctie oft ordinancie der ghetalen beghint van rechter hant also dat
een yegelicke figuere aen die eerste plaetse sijnde natuerlick
rechter hant also dat
een yegelicke figuere aen die eerste plaetse sijnde natuerlick oorspronc hout .1. een
.2. twee .3. drye .4. viere .5. vijf .6. sesse .7. seuen .8. achte .9. neghen.
E
oorspronc hout .1. een
.2. twee .3. drye .4. viere .5. vijf .6. sesse .7. seuen .8. achte .9. neghen.
E der an
der an plaetse gheuet een
yegelicke ghenoede figuere sijn bediedinge thien werf. Maer aen de derde
plaetse
hon
plaetse gheuet een
yegelicke ghenoede figuere sijn bediedinge thien werf. Maer aen de derde
plaetse
hon t werf /
a
t werf /
a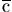 die vierde stede
duysent werf aent welcke is te sett
die vierde stede
duysent werf aent welcke is te sett een punct / e
een punct / e weder te beghinne ghelijcte voor
weder te beghinne ghelijcte voor / also is te mercken
duysent / als ghi dan sien sult in dese na ghescreu
/ also is te mercken
duysent / als ghi dan sien sult in dese na ghescreu figuer
figuer ind
ind exempel.
exempel.
 Die derde Reghele.
Int wtspreken der ghetalen is te beghinnen van
Die derde Reghele.
Int wtspreken der ghetalen is te beghinnen van slinckerhant.
slinckerhant.
 Die vierde Reghele.
Het sullen (wtghenomen hondert) altoos twee figueren / so si alle beyde
bediedelic sijn met malc
Die vierde Reghele.
Het sullen (wtghenomen hondert) altoos twee figueren / so si alle beyde
bediedelic sijn met malc nderen
wtgesproken werden.
nderen
wtgesproken werden.
 Exemplum.
Exemplum.
9 8 7 6 5 4 3 2 1 0
Segghet neghen duysent duysentwerf duysent /
achthondertwerfduysent duysent / sessentseuentichwerf duysent duysent
/vijfhondert duysent / drie en veertich duysent / twee hondert e thiene.
thiene.
 Additie / vergaderinghe / oft
sommeringhe.
Teekent eerst de somme vanden ghetale.
Additie / vergaderinghe / oft
sommeringhe.
Teekent eerst de somme vanden ghetale.
 Die eerste Reghele.
Siet toe dat de figuer
Die eerste Reghele.
Siet toe dat de figuer ghelijc
staen bouen malc
ghelijc
staen bouen malc deren
[fo.2. recto]
also dat de eerste si ghestelt bov
deren
[fo.2. recto]
also dat de eerste si ghestelt bov de eerste e
de eerste e d
d der bouen dander .o
der bouen dander .o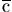 . e
. e een linie daer on
een linie daer on ghetrocken onder welc
wert ghestelt dye somme van
ghetrocken onder welc
wert ghestelt dye somme van figuer
figuer die boven staen.
die boven staen.
4 8 9 6
2 6 1 3
 Die tweede Reghele.
Neemt dat beginsel vander rechter hant / e
Die tweede Reghele.
Neemt dat beginsel vander rechter hant / e doet te samen al dat
ghetal die daer sta
doet te samen al dat
ghetal die daer sta / aen die eerste plaetse / also dicwils als daer com
/ aen die eerste plaetse / also dicwils als daer com inde tsamen voegingen
twee figuer
inde tsamen voegingen
twee figuer /so
scrijft dye eerste / e
/so
scrijft dye eerste / e hout die
ander inden sin / e
hout die
ander inden sin / e die sult ghi
vergaderen metter naester / e
die sult ghi
vergaderen metter naester / e dan
suldi weder
voortdoen ghelijck te vooren / e
dan
suldi weder
voortdoen ghelijck te vooren / e also voort met allen anderen.
also voort met allen anderen.
4 8 9 6
2 6 1 3
7 5 0 8
 Die derde reghele.
Ten lesten en is niet inden sin te houdene. Maer het sal al ghescreven werden
als.
Die derde reghele.
Ten lesten en is niet inden sin te houdene. Maer het sal al ghescreven werden
als.
10 4 3 2 1
10 8 7 6 5
1 1 3 0 8 6
 Die maniere van te spreken.
Hebt altijt inden mont dat woort e
Die maniere van te spreken.
Hebt altijt inden mont dat woort e oft tot / als / 3 / tot 4 oft v 4 e
oft tot / als / 3 / tot 4 oft v 4 e 3
maken .7.
3
maken .7.
 Die vierde Reghele.
Als ghi adderen wilt 97546 / tot 54679 / so stelt dese 2 ghetal
Die vierde Reghele.
Als ghi adderen wilt 97546 / tot 54679 / so stelt dese 2 ghetal deen bouen
dan
deen bouen
dan / e
/ e segt 9 en 6 maect 15. stelt 5 onder de
linie e
segt 9 en 6 maect 15. stelt 5 onder de
linie e hout 1 inden sin.
Om mede te tellen met 7 e
hout 1 inden sin.
Om mede te tellen met 7 e 4. Nu
segt 7 e
4. Nu
segt 7 e 4 maect 11 / hier toe
addeert u 1
inden sin coemt 12 / daer
4 maect 11 / hier toe
addeert u 1
inden sin coemt 12 / daer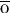 stelt 2
achter 5 on
stelt 2
achter 5 on de linie / e
de linie / e hout noch een
ind
hout noch een
ind sin. Nu segt
[fo.2. verso]
6 e
sin. Nu segt
[fo.2. verso]
6 e 5 maect 11 e
5 maect 11 e 1 inde sin is we
1 inde sin is we 12
daerom sedt weder 2 on
12
daerom sedt weder 2 on 6
e
6
e achter 2 die ghi laetst steldet
onder dye linie
e
achter 2 die ghi laetst steldet
onder dye linie
e hout we
hout we 1 inden sin. Nv segt 4
e
1 inden sin. Nv segt 4
e 7 maect weder 11
e
7 maect weder 11
e 1 inden sin maect
12. Nv stelt 2 on
1 inden sin maect
12. Nv stelt 2 on 4 e
4 e hout 1 ind
hout 1 ind sin. Ten leste so 5 e
sin. Ten leste so 5 e 9 maect 14 e
9 maect 14 e 1
ind
1
ind sin maect 15 / dye stelt
gheheel wt als 5 on
sin maect 15 / dye stelt
gheheel wt als 5 on 5 e
5 e 1 daer achter / ten
laetsten en hout m
1 daer achter / ten
laetsten en hout m inden sin niet /
om dies wille datter ghe
inden sin niet /
om dies wille datter ghe figueren
meer te adderen sijn.
figueren
meer te adderen sijn.
|
| 9 7 5 4 6
|
|
| 5 4 6 7 9
|
| 1
| 5 2 2 2 5
|
 Die vijfste Reghele.
U wildt versam
Die vijfste Reghele.
U wildt versam drie sommen oft
meer. Als ic wil adder
drie sommen oft
meer. Als ic wil adder tesamen
5479 e
tesamen
5479 e 9687
e
9687
e 5984. So stellic dese drie
somm
5984. So stellic dese drie
somm deen bouen dan
deen bouen dan / e
/ e ick segge 4 e
ick segge 4 e 7
maect 11 e
7
maect 11 e 9 maect
20 / daer
9 maect
20 / daer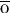 so stellic 0 onder 4
e
so stellic 0 onder 4
e hout 2 ind
hout 2 ind sin /
want voor elcke thiene moet een ind
sin /
want voor elcke thiene moet een ind sin behoud
sin behoud sijn / daer na segt 8 e
sijn / daer na segt 8 e 8
is 16 daer toe addeert 7 maect 21 / hier toe brengt u 2 ind
8
is 16 daer toe addeert 7 maect 21 / hier toe brengt u 2 ind sin is 25 / stelt
5 on
sin is 25 / stelt
5 on 8 e
8 e hout we
hout we 2 inden sin /daer na segt 9 e
2 inden sin /daer na segt 9 e 6 is 15 e
6 is 15 e 4 coemt 19.
Hier toe addeert u 2 inden sin co
4 coemt 19.
Hier toe addeert u 2 inden sin co t
21 stelt 1 on
t
21 stelt 1 on 9 e
9 e hout 2 ind
hout 2 ind sin /
ten laetsten segt 5 e
sin /
ten laetsten segt 5 e 9 is 14 en 5
is 19 / hier toe addeert u 2 ind
9 is 14 en 5
is 19 / hier toe addeert u 2 ind sin
coemt 21 / stelt 1 on
sin
coemt 21 / stelt 1 on 5 e
5 e 2 daer achter e
2 daer achter e is ghedaen also ghi hier stelt
wt exemplum.
is ghedaen also ghi hier stelt
wt exemplum.
|
| 5 4 7 9
| 0
|
|
| 9 6 8 7
| +
|
|
| 5 9 8 4
| 0
|
| 2
| 1 1 5 0
|
|
 Proba van deser specie.
Om te proeue oft wel ghewrocht is so deelt dye .3. somm
Proba van deser specie.
Om te proeue oft wel ghewrocht is so deelt dye .3. somm doer 9 te weten de
simpel n
doer 9 te weten de
simpel n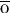 mers e
mers e segt [fo.3. recto] 5 en 4 is 9 worpt altijt
de 9 wech daer
nae hebt ghi 7 en maect 16 de 9 daer wt / blijft 7 / nu 9 en 7 rest noch 7 nu 7
en 6 is 13 de 9 wech / blijft 4 nu 4 en 8 is 12 de 9 wech blijft 3 nu 3 en 7 is
10 blijft 1 nu 1 en 5 is 6 nu 6 en 9 blijft 6 nu 6 en 8 is 14 blijft 5 nu 5 en
4 rest 0 voor deerste proeve. Nu 2 en 1 is 3 en 1 is 4 en 5 is 9 e
segt [fo.3. recto] 5 en 4 is 9 worpt altijt
de 9 wech daer
nae hebt ghi 7 en maect 16 de 9 daer wt / blijft 7 / nu 9 en 7 rest noch 7 nu 7
en 6 is 13 de 9 wech / blijft 4 nu 4 en 8 is 12 de 9 wech blijft 3 nu 3 en 7 is
10 blijft 1 nu 1 en 5 is 6 nu 6 en 9 blijft 6 nu 6 en 8 is 14 blijft 5 nu 5 en
4 rest 0 voor deerste proeve. Nu 2 en 1 is 3 en 1 is 4 en 5 is 9 e rest ooc 0
e
rest ooc 0
e is wel gewrocht. Doet also na
alderh
is wel gewrocht. Doet also na
alderh de ghetale van lb.gy.
v
de ghetale van lb.gy.
v gul
gul . v
. v f.gy. Env
f.gy. Env gewicht
gewicht pond
pond / marck
/ marck / onc
/ onc . te weten van elcx bisonder.
. te weten van elcx bisonder.
 Substractie oft aftreckinghe.
Openbaert die reghele te substraher
Substractie oft aftreckinghe.
Openbaert die reghele te substraher oft af te trecken /
deen ghetal vand
oft af te trecken /
deen ghetal vand ander
ander dat daer wert ghesien het
ouerbliju
dat daer wert ghesien het
ouerbliju /in welck
gehouden sal worden die eerste reghele der addici
/in welck
gehouden sal worden die eerste reghele der addici /ghelijc als of ick wil
trecken 364 van 485 stellet aldus
/ghelijc als of ick wil
trecken 364 van 485 stellet aldus
4 8 5
3 6 4
 Een sekeringhe.
Het onderste getal en sal niet meerder zijn d
Een sekeringhe.
Het onderste getal en sal niet meerder zijn d dat opperste /maer si mach haer
wel ghelyc zijn als.
dat opperste /maer si mach haer
wel ghelyc zijn als.
 Die tweede reghele.
Beghint aen de rechte hant / ne
Die tweede reghele.
Beghint aen de rechte hant / ne t
een figuere vanden ander
t
een figuere vanden ander / e
/ e wat daer d
wat daer d blijft stelt onder de linie ghelijck
blijft stelt onder de linie ghelijck
| 9 8 2 7
| Segt 5 van 7 rest 2
die
|
| 6 5 0 5
|
scrijft onder de linie / nv 0 van 2 rest 2 scrijft ooc onderde linie ter
slincker hant waert / dan 5 v 8
rest 3 scrijft ooc v
8
rest 3 scrijft ooc v gelijcken dan 6
van 9
blijft ooc 3 scrijft ooc desghelijcx e
gelijcken dan 6
van 9
blijft ooc 3 scrijft ooc desghelijcx e is ghemaect.
is ghemaect.
 Die derde reghele.
So w
Die derde reghele.
So w neer dat ghi die onderste
figuere v
neer dat ghi die onderste
figuere v der op verste nieten
moecht trecken
/ so ne
der op verste nieten
moecht trecken
/ so ne t een vander [fo.3. verso]
naerster figuer
t een vander [fo.3. verso]
naerster figuer ter slincker dat
waert /
e
ter slincker dat
waert /
e sal zijn 10 e
sal zijn 10 e addeerter de figuere toe die te cleene
was om de onderste
daeraf te trecken / ghelijc ic wil treck
addeerter de figuere toe die te cleene
was om de onderste
daeraf te trecken / ghelijc ic wil treck 6892 van 9721 stellet aldus
6892 van 9721 stellet aldus
| 9 7 2 1
| Nu trect 2
van1
|
| 6 8 9 2
|
dat en mach niet zijn maer ic neme 2 van 10 so blijft 8 e 1 dat is tghetal
v
1 dat is tghetal
v welck ghi 2 niet en const
ghetrecken / daeraf co
welck ghi 2 niet en const
ghetrecken / daeraf co t 9 die sedt
on
t 9 die sedt
on 2 voort
addeert 1 tot 9 co
2 voort
addeert 1 tot 9 co t 10 /e
t 10 /e 10 van 10 blijft 0 / daer toe addeert 2
die set
on
10 van 10 blijft 0 / daer toe addeert 2
die set
on de linie / e
de linie / e tot dat naeste getal als 8 tot 1
word
tot dat naeste getal als 8 tot 1
word 9. Segt 9 van 7 dat
en c
9. Segt 9 van 7 dat
en c niet ghesijn / maer van 10
blijft 1 e
niet ghesijn / maer van 10
blijft 1 e 7 word
7 word 8 die scrijft onder 8
ten lesten gheeft 1 tot 6 maect 7 e
8 die scrijft onder 8
ten lesten gheeft 1 tot 6 maect 7 e 7 ghetrock
7 ghetrock van 9 Reste 2 e
van 9 Reste 2 e staet
aldus
staet
aldus
| 9 7 2 1
| I
|
| 6 8 9 2
| +
|
| 2 8 2 9
| I
|
 Die maniere van spreken.
Neemt voor u dat woort als 6 van 8 blijft 2.
Die maniere van spreken.
Neemt voor u dat woort als 6 van 8 blijft 2.
 Een ander maniere van substractie
de vierde regel.
It
Een ander maniere van substractie
de vierde regel.
It wildi treck
wildi treck 3008906 van 5006004
stelt deen bou
3008906 van 5006004
stelt deen bou dander als voren e
dander als voren e beghint van
beghint van slincker
hant. Segt 3 v
slincker
hant. Segt 3 v 5
blijft 2 die sou di on
5
blijft 2 die sou di on stellen waert
dat dye on
stellen waert
dat dye on ste somme niet
meer
ste somme niet
meer en bleue d
en bleue d de opperste / mer om datse meer
de opperste / mer om datse meer blijftso laet bou
blijftso laet bou de 5 een eenk
de 5 een eenk staen e
staen e doet de 5 wt met e
doet de 5 wt met e streepk
streepk / e
/ e stelt 1 on
stelt 1 on 3 e
3 e gaet een figure voort
e
gaet een figure voort
e segt 0 v
segt 0 v 10 blijft altijts 10
daer
10 blijft altijts 10
daer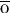 een figure voort
e
een figure voort
e sedt 9 on
sedt 9 on neffens 1 dan trect die
9 v
neffens 1 dan trect die
9 v die opperste
10. Rest 1 dit stelt bouen 0 om de cause voorseyt dan gaet een figuere voort /
e
die opperste
10. Rest 1 dit stelt bouen 0 om de cause voorseyt dan gaet een figuere voort /
e trect 0 van 10
sedt 9 onder laet 1 bou
trect 0 van 10
sedt 9 onder laet 1 bou als voren
/ gaet noch voort / e
als voren
/ gaet noch voort / e trect 8 v
trect 8 v 16 blijft 8 stelt 7
on
16 blijft 8 stelt 7
on e
e laet 1 bouen die 6 e
laet 1 bouen die 6 e doerstreept de 6 /daer
na trect 9 v
doerstreept de 6 /daer
na trect 9 v 10
Rest 1 stelt dat 1 bou
10
Rest 1 stelt dat 1 bou om de
cause [fo.4. recto] als voren e
om de
cause [fo.4. recto] als voren e stelt 0 onder e
stelt 0 onder e dan gaet voort e
dan gaet voort e trect 0 van 10 blijft 10
/ stelt we
trect 0 van 10 blijft 10
/ stelt we 9 onder
e
9 onder
e bou
bou daer nae ten lest
daer nae ten lest trect 6 v
trect 6 v 14 Rest 8 die sedt
on
14 Rest 8 die sedt
on e
e also rest v als ghi
trect 3008006 v
also rest v als ghi
trect 3008006 v 5006004 reste 1997998 also ghi hier siet int exempl
5006004 reste 1997998 also ghi hier siet int exempl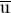 .
.
| 5 0 0 6 0 0 4
|
| Schult
|
| 3 0 0 8 0 0 6
|
| Betalinghe.
|
| 1 9 9 7 9 9 8
|
| Reste
|
Proba
Om te wet oft ghi
wel ghesubstraheert hebt. So addeert beyde de laetste somm
oft ghi
wel ghesubstraheert hebt. So addeert beyde de laetste somm te sam
te sam als betalinge e
als betalinge e reste e
reste e commet ghelijc die opperste somme te
wet
commet ghelijc die opperste somme te
wet de schult so yst
welgheda
de schult so yst
welgheda als dat blijct hier
onder.
als dat blijct hier
onder.
|
| 3 0 0 8 0 0 6
|
| Getal.
|
|
| 1 9 9 7 9 9 8
|
| Reste.
|
| Proeve.
| 5 0 0 6 0 0 4
|
| Schult
|
 Multiplicatie is hier ghedeylt inses
reghelen.
Multiplicatie is deen ghetal v
Multiplicatie is hier ghedeylt inses
reghelen.
Multiplicatie is deen ghetal v menighen met een ander ghetal / dat is
also veel
als den multiplicateur / of multipliceer
menighen met een ander ghetal / dat is
also veel
als den multiplicateur / of multipliceer in h
in h selven beuangt. So menich
werf te augmenteren oft menichfuldigen d
selven beuangt. So menich
werf te augmenteren oft menichfuldigen d nommer d
nommer d welcken ghemultipliceert
moet werd
welcken ghemultipliceert
moet werd . Exemplum. Ic wil
multiplicer
. Exemplum. Ic wil
multiplicer 3 met 2 e
3 met 2 e ic segge 3 werf 2 is 6
de 3 is d
ic segge 3 werf 2 is 6
de 3 is d multiplicator e
multiplicator e de 2 d
de 2 d nommer d
nommer d welck
welck ghemultipliceert moet
werd
ghemultipliceert moet
werd . E
. E om alle multiplicatie te do
om alle multiplicatie te do die on
die on tiene sijn / so heb ic
ghestelt een tafelk
tiene sijn / so heb ic
ghestelt een tafelk daer bi
datm
daer bi
datm terstont vind
terstont vind sal de multiplicacie v
sal de multiplicacie v 1
tot alle die figuer
1
tot alle die figuer totter
neghenster toe. Exempel. Ic wil multiplier
totter
neghenster toe. Exempel. Ic wil multiplier 7
werf 9 so neme ic 9 aen de slincke hant e
7
werf 9 so neme ic 9 aen de slincke hant e gae voort tot on
gae voort tot on 7 die bou
7 die bou int
opperste staet so vind ic 63 so veel maect 7 werf 9 e
int
opperste staet so vind ic 63 so veel maect 7 werf 9 e doet also van alle an
doet also van alle an ghelijck
ghelijck e
e dit is goet
dit is goet 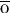 iongers die eerst leeren [fo.4.
verso]
iongers die eerst leeren [fo.4.
verso]
| 1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
|
| 2
| 4
| 6
| 8
| 10
| 12
| 14
| 16
| 18
|
| 3
| 6
| 9
| 12
| 15
| 18
| 21
| 24
| 27
|
| 4
| 8
| 12
| 16
| 20
| 24
| 28
| 32
| 36
|
| 5
| 10
| 15
| 20
| 25
| 30
| 35
| 40
| 45
|
| 6
| 12
| 18
| 24
| 30
| 36
| 42
| 48
| 54
|
| 7
| 14
| 21
| 28
| 35
| 42
| 49
| 56
| 63
|
| 8
| 16
| 24
| 32
| 40
| 48
| 56
| 64
| 72
|
| 9
| 18
| 27
| 36
| 45
| 54
| 63
| 72
| 81
|
 Die eerste reghele.
Item wilde multiplicer
Die eerste reghele.
Item wilde multiplicer 2
figuer
2
figuer met eender figuere / als 24
met 4 so stelt 24 bouen e
met eender figuere / als 24
met 4 so stelt 24 bouen e 4
onder / e
4
onder / e segt 4 werf 4 is 16 /
stelt 6 on
segt 4 werf 4 is 16 /
stelt 6 on e
e hout 1 ind
hout 1 ind sin / daer na segt 4 werf 2 is 8 / hier
toe addeert 1 ind
sin / daer na segt 4 werf 2 is 8 / hier
toe addeert 1 ind sin co
sin co t 9 die 9 set achter 6 co
t 9 die 9 set achter 6 co t 96 so veel maect 4 werf 24 waer af de
si figuere hier na volghet.
t 96 so veel maect 4 werf 24 waer af de
si figuere hier na volghet.
 Die tweede reghel.
Vvildi multiplicer
Die tweede reghel.
Vvildi multiplicer 2 figuer
2 figuer oft meer / met 2 figuren oft meer / als
ick wil multiplieren 25 met 36 stelt de
oft meer / met 2 figuren oft meer / als
ick wil multiplieren 25 met 36 stelt de bou
bou dan
dan als vor
als vor e
e segt 6 werf 5 is 30 stelt 0 on
segt 6 werf 5 is 30 stelt 0 on 6 e
6 e hout 3 ind
hout 3 ind sin / daer na segt 6 werf 2 is 12
e
sin / daer na segt 6 werf 2 is 12
e 3 ind
3 ind sin is 15 / die stelt al achter 0 / daer na
multipliceert metter 3 dat is met 30 e
sin is 15 / die stelt al achter 0 / daer na
multipliceert metter 3 dat is met 30 e segt 3 werf 5 is 15. Stelt de 5
een
segt 3 werf 5 is 15. Stelt de 5
een graet voor
graet voor achterwaert te wet
achterwaert te wet onder 5 / e
onder 5 / e hout 1 ind
hout 1 ind sin / dan segt 3 werf 2 is 6 / daer toe
addeert u 1 ind
sin / dan segt 3 werf 2 is 6 / daer toe
addeert u 1 ind sin co
sin co t 7 die stelt on
t 7 die stelt on 1 achter 5 daer na adderet de 2
somm
1 achter 5 daer na adderet de 2
somm te sam
te sam coemt 900 waer af die figuere
[fo. 5 recto]
hier na volgt.
coemt 900 waer af die figuere
[fo. 5 recto]
hier na volgt.
|
| 2
| 5
|
|
| 2
| 5
|
|
| 3
| 6
|
|
| 3
| 6
|
| 1
| 5
| 0
|
| 1
| 5
| 0
|
|
|
|
|
| 7
| 5
|
|
|
|
|
|
| 9
| 0
| 0
|
 Die derde reghele.
Item wilde multiplicer
Die derde reghele.
Item wilde multiplicer veel
figuer
veel
figuer met malcander
met malcander als ic wil multiplicer
als ic wil multiplicer 5378 met 6795. So stelt beyde
ghetal
5378 met 6795. So stelt beyde
ghetal deen bou
deen bou dander / so hier on
dander / so hier on volget / e
volget / e segt 5 werf 8 is 40 / stelt 0 onder 5
e
segt 5 werf 8 is 40 / stelt 0 onder 5
e hout 4 inden sin / daer na segt
we
hout 4 inden sin / daer na segt
we 5 werf 7 is 35 e
5 werf 7 is 35 e 4 ind
4 ind sin maect 39 / stelt 9 on
sin maect 39 / stelt 9 on 9 e
9 e hout 3 ind
hout 3 ind sin / daer na segt 5 werf 3 is 15
e
sin / daer na segt 5 werf 3 is 15
e 3 ind
3 ind sin is 18 / stelt 8 on
sin is 18 / stelt 8 on 7 e
7 e hout 1 ind
hout 1 ind sin ten laetsten segt 5 werf 5 es 25
e
sin ten laetsten segt 5 werf 5 es 25
e 1 ind
1 ind sin is 26 / stelt gheheel achter de 8
e
sin is 26 / stelt gheheel achter de 8
e coemt dan aldus.
coemt dan aldus.
|
| 5
| 3
| 7
| 8
|
|
| 6
| 7
| 9
| 5
|
| 2
| 5
| 8
| 9
| 0
|
Dan so multipliceert metter 9 maer dese multiplicacie moet een graet achterwaert sta
graet achterwaert sta / om dieswille datse staet inde plaetse
v
/ om dieswille datse staet inde plaetse
v 10. Nu segt 9 werf 8 is 72 /
sedt 2 on
10. Nu segt 9 werf 8 is 72 /
sedt 2 on 9 e
9 e hout 7 ind
hout 7 ind sin / d
sin / d multipliceert voort totter lester figuere
soot hier voorseyt is co
multipliceert voort totter lester figuere
soot hier voorseyt is co t voer de
multiplicacie van 9 coemt 48402 / e
t voer de
multiplicacie van 9 coemt 48402 / e staet dan aldus.
staet dan aldus.
|
|
| 5
| 3
| 7
| 8
|
|
|
| 6
| 7
| 9
| 5
|
|
| 2
| 5
| 8
| 9
| 0
|
| 4
| 8
| 4
| 0
| 2
|
|
Daer naer multipliceert metter 7 e segt 7 werf 8 is 56 / stelt on
segt 7 werf 8 is 56 / stelt on 0
e
0
e hout 5 ind
hout 5 ind sin e
sin e werct also achteruolghende als
vor
werct also achteruolghende als
vor coemt voor dye multiplicacie
van
[fo. 5 verso]
7 . 37646 / daer na werct metter laetster figuere met 6 in al
coemt voor dye multiplicacie
van
[fo. 5 verso]
7 . 37646 / daer na werct metter laetster figuere met 6 in al manieren als voren e
manieren als voren e 6 werf 8 is 48 / stelt 8 onder 4 e
6 werf 8 is 48 / stelt 8 onder 4 e voort alsoot voorseyt is / co
voort alsoot voorseyt is / co t 32268 e
t 32268 e staet als hier na volght / dan addeert de
4 on
staet als hier na volght / dan addeert de
4 on ste somm
ste somm te samen co
te samen co t 36543510 alsoot blijct hier on
t 36543510 alsoot blijct hier on int exempl
int exempl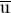 .
.
|
|
|
| 5
| 3
| 7
| 8
|
|
|
|
|
| 5
| 3
| 7
| 8
|
|
|
|
| 6
| 7
| 9
| 5
|
|
|
|
|
| 6
| 7
| 9
| 5
|
|
|
| 2
| 5
| 8
| 9
| 0
|
|
|
|
| 2
| 5
| 8
| 9
| 0
|
|
| 4
| 8
| 4
| 0
| 2
|
|
|
|
| 4
| 8
| 4
| 0
| 2
|
|
| 3
| 7
| 6
| 4
| 6
|
|
|
|
| 3
| 7
| 6
| 4
| 6
|
|
|
|
|
|
|
|
|
|
|
| 3
| 2
| 2
| 6
| 8
|
|
|
|
|
|
|
|
|
|
|
|
| 3
| 6
| 5
| 4
| 3
| 5
| 1
| 0
|
 Die vierde reghel v
Die vierde reghel v multiplicatie een an
multiplicatie een an maniere
maniere
Vvildi multiplicer 3576 met 6358.
So multipliceert 3576 met 6 dwelc is die leste figuere vander ander somme
co
3576 met 6358.
So multipliceert 3576 met 6 dwelc is die leste figuere vander ander somme
co t 21456 hier voren set 000
figueren om dieswille dat 6 / 3 figuer
t 21456 hier voren set 000
figueren om dieswille dat 6 / 3 figuer voer haer heeft coemt 21456000 / daer
nae multipliceert 3576 met 3 coemt 10728 / hier voren stelt 00 figuer
voer haer heeft coemt 21456000 / daer
nae multipliceert 3576 met 3 coemt 10728 / hier voren stelt 00 figuer 00 / om dat voor 3 maer 2 figuer
00 / om dat voor 3 maer 2 figuer en staen co
en staen co t 1072800 / daer na multipliceert 3576
met 5 co
t 1072800 / daer na multipliceert 3576
met 5 co t 17880 / stelt hier een
figure voor 0 co
t 17880 / stelt hier een
figure voor 0 co t 178800 / daer
na multipliceert metter lester figuere dat is 8 co
t 178800 / daer
na multipliceert metter lester figuere dat is 8 co t 28608 / nv addeert dese vier
somm
t 28608 / nv addeert dese vier
somm te sam
te sam / als 21456000 e
/ als 21456000 e 21456000 e
21456000 e 1072800 e
1072800 e 178800 e
178800 e 28608 coemt te samen 22736208.
28608 coemt te samen 22736208.
|
|
|
|
| 3
| 5
| 7
| 6
|
|
|
|
|
|
|
|
| 6
| 3
| 5
| 8
|
|
|
|
| 2
| 1
| 4
| 5
| 6
| 0
| 0
| 0
|
| 3
|
|
|
| 1
| 0
| 7
| 2
| 8
| 0
| 0
|
| 3 + 3
|
|
|
|
| 1
| 7
| 8
| 8
| 0
| 0
|
| 4
| 12
|
|
|
|
| 2
| 8
| 6
| 0
| 8
|
|
|
|
| 2
| 2
| 7
| 3
| 6
| 2
| 0
| 8
|
|
|
|
[fol. 6 recto]
 Die vijfste reghel noch een ander
maniere van multiplicatie.
Vvildi multiplicer
Die vijfste reghel noch een ander
maniere van multiplicatie.
Vvildi multiplicer 25 met 34 so
stelt deen bou
25 met 34 so
stelt deen bou dan
dan als voren e
als voren e segt 4 werf 5 is 20 / stelt 0 e
segt 4 werf 5 is 20 / stelt 0 e hout 2 ind
hout 2 ind sin / daer na segt 4 werf 2 is 8 e
sin / daer na segt 4 werf 2 is 8 e 2 ind
2 ind sin co
sin co t 10 die hout ooc ind
t 10 die hout ooc ind sin / daer na multipliceert 25 met 3
e
sin / daer na multipliceert 25 met 3
e segt 3 werf 5 is 15 e
segt 3 werf 5 is 15 e 10 ind
10 ind sin coemt 25 / set 5 achter 0 e
sin coemt 25 / set 5 achter 0 e hout 2 ind
hout 2 ind sin / daer na segt 3 werf 2 is 6 e
sin / daer na segt 3 werf 2 is 6 e 2 inden sin coemt 8 die stelt achter 5
e
2 inden sin coemt 8 die stelt achter 5
e coemt 850 / e
coemt 850 / e is ghemaect.
is ghemaect.
 Die seste reghele.
Om te multiplicer
Die seste reghele.
Om te multiplicer sommen daer
veel cyfers voor staen als wildi multiplicer
sommen daer
veel cyfers voor staen als wildi multiplicer 2100 met 34000 so multipliceert 21
met 34 co
2100 met 34000 so multipliceert 21
met 34 co t 714 daer toe stelt
also vele cyfers voor
t 714 daer toe stelt
also vele cyfers voor als aen
beyde de sommen staen dat syn 00000 co
als aen
beyde de sommen staen dat syn 00000 co t 71400000 / doet desghelijcx van
ander.
t 71400000 / doet desghelijcx van
ander.
|
| 2
| 1
|
|
|
|
| 3
| 4
|
|
|
|
| 8
| 4
|
| | 00000 coemt 71400000
|
| 6
| 3
|
|
|
|
| 7
| 1
| 4
|
|
|
 Die proeue van multiplicatie.
Om te proeu
Die proeue van multiplicatie.
Om te proeu oft ghi wel
ghemultipliceert hebt / so deylt beyde dopperste somm
oft ghi wel
ghemultipliceert hebt / so deylt beyde dopperste somm de simpel n
de simpel n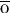 mers bi 9 elcke somme bison
mers bi 9 elcke somme bison e
e werpt de 9 altijts wech e
werpt de 9 altijts wech e de reste v
de reste v elcke somme multipliceert te sam
elcke somme multipliceert te sam / e
/ e vand
vand producte werpt ooc de 9 wech e
producte werpt ooc de 9 wech e de reste stelt opt cruce / exempel. Ic wil
proeu
de reste stelt opt cruce / exempel. Ic wil
proeu oft de leste multiplicacie op
2 na goet is so neme ick beyde dye opperste sommen als 3576 e
oft de leste multiplicacie op
2 na goet is so neme ick beyde dye opperste sommen als 3576 e 6358 e
6358 e segghe 3 e
segghe 3 e 5 is 8 e
5 is 8 e 7
[fol. 6 verso]
coemt 15 e
7
[fol. 6 verso]
coemt 15 e 9 vvt / rest 6 e
9 vvt / rest 6 e 6 coemt 12 de 9 vvt blijft 3 die stelt
opt cruyce / daer na deylt oft telt de 9 vvt 6358 e
6 coemt 12 de 9 vvt blijft 3 die stelt
opt cruyce / daer na deylt oft telt de 9 vvt 6358 e segt 6 e
segt 6 e 3 is 9 blijft niet / daer na 5 e
3 is 9 blijft niet / daer na 5 e 8 is 13 e
8 is 13 e 9 vvt blijft 4 die stelt on
9 vvt blijft 4 die stelt on cruyce e
cruyce e multipliceert 3 met 4 co
multipliceert 3 met 4 co t 12 daer 9 vvt blijft 3 stelt 3 ter
sid
t 12 daer 9 vvt blijft 3 stelt 3 ter
sid aen tcruyce / d
aen tcruyce / d ouertelt die figuer
ouertelt die figuer van der lester somme die ghesuecedeert
is vvter multiplicatie / als 22736208 / e
van der lester somme die ghesuecedeert
is vvter multiplicatie / als 22736208 / e segt 2 e
segt 2 e 2 is 4 e
2 is 4 e 7 is 11 de 9 wech blijft 2 e
7 is 11 de 9 wech blijft 2 e 3 is 5 e
3 is 5 e 6 is 11 de 9 vvt blijft ooc 2 e
6 is 11 de 9 vvt blijft ooc 2 e 2 is 4 e
2 is 4 e 8 is 12 dye 9 wech blijft 3 die stelt op
dan
8 is 12 dye 9 wech blijft 3 die stelt op
dan side vand
side vand cruyce co
cruyce co t ghelijck op deen side vand
t ghelijck op deen side vand cruyce staet e
cruyce staet e is wel gheda
is wel gheda . Mer alst onghelijc co
. Mer alst onghelijc co t so bethoget dat qualijck ghewrocht is /
doet aldus van alle ander multiplicatien.
t so bethoget dat qualijck ghewrocht is /
doet aldus van alle ander multiplicatien.
. . . . .
Ga naar het vervolg van de tekst
 Die tweede Reghele.
Die tweede Reghele.
 Dat eerste deel vander Rekeninghe
Numeracie / oft
tellinghe.
Dat eerste deel vander Rekeninghe
Numeracie / oft
tellinghe. scrijft / als
.1.2.3.4.5.6.7.8.9. En de thiende is een onbediedelijcke als 0, nullio ghenaemt
/ de welcke voor haerselu
scrijft / als
.1.2.3.4.5.6.7.8.9. En de thiende is een onbediedelijcke als 0, nullio ghenaemt
/ de welcke voor haerselu niet en
bediet. Maer w
niet en
bediet. Maer w neer si wert
ghestelt voor die bediedelicke tegen die rechte
h
neer si wert
ghestelt voor die bediedelicke tegen die rechte
h t so bringet si
een yegelijcx ghetal bediedende thien werf also veel als in dese exempele, 24 is
vier en [fo.1. verso] twintich. Stelt een .0. daervoor
t so bringet si
een yegelijcx ghetal bediedende thien werf also veel als in dese exempele, 24 is
vier en [fo.1. verso] twintich. Stelt een .0. daervoor als .240. so hebt ghi
twee hon
als .240. so hebt ghi
twee hon t e
t e veertich. Ooc so veruult
si de lege plaetse / als oft ic wilde scriv
veertich. Ooc so veruult
si de lege plaetse / als oft ic wilde scriv duysentvijfhon
duysentvijfhon t e
t e twintich so settick voor
dit ghetal die onder thien sijn / welc daer gheen en is / een nulla e
twintich so settick voor
dit ghetal die onder thien sijn / welc daer gheen en is / een nulla e staet aldus .1520.
staet aldus .1520. Die tweede Reghele.
Die tweede Reghele.
 rechter hant also dat
een yegelicke figuere aen die eerste plaetse sijnde natuerlick
rechter hant also dat
een yegelicke figuere aen die eerste plaetse sijnde natuerlick oorspronc hout .1. een
.2. twee .3. drye .4. viere .5. vijf .6. sesse .7. seuen .8. achte .9. neghen.
E
oorspronc hout .1. een
.2. twee .3. drye .4. viere .5. vijf .6. sesse .7. seuen .8. achte .9. neghen.
E der an
der an plaetse gheuet een
yegelicke ghenoede figuere sijn bediedinge thien werf. Maer aen de derde
plaetse
hon
plaetse gheuet een
yegelicke ghenoede figuere sijn bediedinge thien werf. Maer aen de derde
plaetse
hon t werf /
a
t werf /
a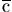 die vierde stede
duysent werf aent welcke is te sett
die vierde stede
duysent werf aent welcke is te sett een punct / e
een punct / e weder te beghinne ghelijcte voor
weder te beghinne ghelijcte voor / also is te mercken
duysent / als ghi dan sien sult in dese na ghescreu
/ also is te mercken
duysent / als ghi dan sien sult in dese na ghescreu figuer
figuer ind
ind exempel.
exempel. Die derde Reghele.
Die derde Reghele.
 slinckerhant.
slinckerhant. Die vierde Reghele.
Die vierde Reghele.
 nderen
wtgesproken werden.
nderen
wtgesproken werden. Exemplum.
Exemplum. thiene.
thiene. Additie / vergaderinghe / oft
sommeringhe.
Additie / vergaderinghe / oft
sommeringhe.
 Die eerste Reghele.
Die eerste Reghele.
 ghelijc
staen bouen malc
ghelijc
staen bouen malc deren
[fo.2. recto]
also dat de eerste si ghestelt bov
deren
[fo.2. recto]
also dat de eerste si ghestelt bov de eerste e
de eerste e d
d der bouen dander .o
der bouen dander .o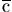 . e
. e een linie daer on
een linie daer on ghetrocken onder welc
wert ghestelt dye somme van
ghetrocken onder welc
wert ghestelt dye somme van figuer
figuer die boven staen.
die boven staen. Die tweede Reghele.
Die tweede Reghele.
 doet te samen al dat
ghetal die daer sta
doet te samen al dat
ghetal die daer sta / aen die eerste plaetse / also dicwils als daer com
/ aen die eerste plaetse / also dicwils als daer com inde tsamen voegingen
twee figuer
inde tsamen voegingen
twee figuer /so
scrijft dye eerste / e
/so
scrijft dye eerste / e hout die
ander inden sin / e
hout die
ander inden sin / e die sult ghi
vergaderen metter naester / e
die sult ghi
vergaderen metter naester / e dan
suldi weder
voortdoen ghelijck te vooren / e
dan
suldi weder
voortdoen ghelijck te vooren / e also voort met allen anderen.
also voort met allen anderen. Die derde reghele.
Die derde reghele.
 Die maniere van te spreken.
Die maniere van te spreken.
 oft tot / als / 3 / tot 4 oft v 4 e
oft tot / als / 3 / tot 4 oft v 4 e 3
maken .7.
3
maken .7. Die vierde Reghele.
Die vierde Reghele.
 deen bouen
dan
deen bouen
dan / e
/ e segt 9 en 6 maect 15. stelt 5 onder de
linie e
segt 9 en 6 maect 15. stelt 5 onder de
linie e hout 1 inden sin.
Om mede te tellen met 7 e
hout 1 inden sin.
Om mede te tellen met 7 e 4. Nu
segt 7 e
4. Nu
segt 7 e 4 maect 11 / hier toe
addeert u 1
inden sin coemt 12 / daer
4 maect 11 / hier toe
addeert u 1
inden sin coemt 12 / daer stelt 2
achter 5 on
stelt 2
achter 5 on de linie / e
de linie / e hout noch een
ind
hout noch een
ind sin. Nu segt
[fo.2. verso]
6 e
sin. Nu segt
[fo.2. verso]
6 e 5 maect 11 e
5 maect 11 e 1 inde sin is we
1 inde sin is we 12
daerom sedt weder 2 on
12
daerom sedt weder 2 on 6
e
6
e achter 2 die ghi laetst steldet
onder dye linie
e
achter 2 die ghi laetst steldet
onder dye linie
e hout we
hout we 1 inden sin. Nv segt 4
e
1 inden sin. Nv segt 4
e 7 maect weder 11
e
7 maect weder 11
e 1 inden sin maect
12. Nv stelt 2 on
1 inden sin maect
12. Nv stelt 2 on 4 e
4 e hout 1 ind
hout 1 ind sin. Ten leste so 5 e
sin. Ten leste so 5 e 9 maect 14 e
9 maect 14 e 1
ind
1
ind sin maect 15 / dye stelt
gheheel wt als 5 on
sin maect 15 / dye stelt
gheheel wt als 5 on 5 e
5 e 1 daer achter / ten
laetsten en hout m
1 daer achter / ten
laetsten en hout m inden sin niet /
om dies wille datter ghe
inden sin niet /
om dies wille datter ghe figueren
meer te adderen sijn.
figueren
meer te adderen sijn. Die vijfste Reghele.
Die vijfste Reghele.
 drie sommen oft
meer. Als ic wil adder
drie sommen oft
meer. Als ic wil adder tesamen
5479 e
tesamen
5479 e 9687
e
9687
e 5984. So stellic dese drie
somm
5984. So stellic dese drie
somm deen bouen dan
deen bouen dan / e
/ e ick segge 4 e
ick segge 4 e 7
maect 11 e
7
maect 11 e 9 maect
20 / daer
9 maect
20 / daer so stellic 0 onder 4
e
so stellic 0 onder 4
e hout 2 ind
hout 2 ind sin /
want voor elcke thiene moet een ind
sin /
want voor elcke thiene moet een ind sin behoud
sin behoud sijn / daer na segt 8 e
sijn / daer na segt 8 e 8
is 16 daer toe addeert 7 maect 21 / hier toe brengt u 2 ind
8
is 16 daer toe addeert 7 maect 21 / hier toe brengt u 2 ind sin is 25 / stelt
5 on
sin is 25 / stelt
5 on 8 e
8 e hout we
hout we 2 inden sin /daer na segt 9 e
2 inden sin /daer na segt 9 e 6 is 15 e
6 is 15 e 4 coemt 19.
Hier toe addeert u 2 inden sin co
4 coemt 19.
Hier toe addeert u 2 inden sin co t
21 stelt 1 on
t
21 stelt 1 on 9 e
9 e hout 2 ind
hout 2 ind sin /
ten laetsten segt 5 e
sin /
ten laetsten segt 5 e 9 is 14 en 5
is 19 / hier toe addeert u 2 ind
9 is 14 en 5
is 19 / hier toe addeert u 2 ind sin
coemt 21 / stelt 1 on
sin
coemt 21 / stelt 1 on 5 e
5 e 2 daer achter e
2 daer achter e is ghedaen also ghi hier stelt
wt exemplum.
is ghedaen also ghi hier stelt
wt exemplum. Proba van deser specie.
Proba van deser specie.
 doer 9 te weten de
simpel n
doer 9 te weten de
simpel n mers e
mers e segt [fo.3. recto] 5 en 4 is 9 worpt altijt
de 9 wech daer
nae hebt ghi 7 en maect 16 de 9 daer wt / blijft 7 / nu 9 en 7 rest noch 7 nu 7
en 6 is 13 de 9 wech / blijft 4 nu 4 en 8 is 12 de 9 wech blijft 3 nu 3 en 7 is
10 blijft 1 nu 1 en 5 is 6 nu 6 en 9 blijft 6 nu 6 en 8 is 14 blijft 5 nu 5 en
4 rest 0 voor deerste proeve. Nu 2 en 1 is 3 en 1 is 4 en 5 is 9 e
segt [fo.3. recto] 5 en 4 is 9 worpt altijt
de 9 wech daer
nae hebt ghi 7 en maect 16 de 9 daer wt / blijft 7 / nu 9 en 7 rest noch 7 nu 7
en 6 is 13 de 9 wech / blijft 4 nu 4 en 8 is 12 de 9 wech blijft 3 nu 3 en 7 is
10 blijft 1 nu 1 en 5 is 6 nu 6 en 9 blijft 6 nu 6 en 8 is 14 blijft 5 nu 5 en
4 rest 0 voor deerste proeve. Nu 2 en 1 is 3 en 1 is 4 en 5 is 9 e rest ooc 0
e
rest ooc 0
e is wel gewrocht. Doet also na
alderh
is wel gewrocht. Doet also na
alderh de ghetale van lb.gy.
v
de ghetale van lb.gy.
v gul
gul . v
. v f.gy. Env
f.gy. Env gewicht
gewicht pond
pond / marck
/ marck / onc
/ onc . te weten van elcx bisonder.
. te weten van elcx bisonder. Substractie oft aftreckinghe.
Substractie oft aftreckinghe.
 oft af te trecken /
deen ghetal vand
oft af te trecken /
deen ghetal vand ander
ander dat daer wert ghesien het
ouerbliju
dat daer wert ghesien het
ouerbliju /in welck
gehouden sal worden die eerste reghele der addici
/in welck
gehouden sal worden die eerste reghele der addici /ghelijc als of ick wil
trecken 364 van 485 stellet aldus
/ghelijc als of ick wil
trecken 364 van 485 stellet aldus Een sekeringhe.
Een sekeringhe.
 dat opperste /maer si mach haer
wel ghelyc zijn als.
dat opperste /maer si mach haer
wel ghelyc zijn als. Die tweede reghele.
Die tweede reghele.
 t
een figuere vanden ander
t
een figuere vanden ander / e
/ e wat daer d
wat daer d blijft stelt onder de linie ghelijck
blijft stelt onder de linie ghelijck 8
rest 3 scrijft ooc v
8
rest 3 scrijft ooc v gelijcken dan 6
van 9
blijft ooc 3 scrijft ooc desghelijcx e
gelijcken dan 6
van 9
blijft ooc 3 scrijft ooc desghelijcx e is ghemaect.
is ghemaect. Die derde reghele.
Die derde reghele.
 neer dat ghi die onderste
figuere v
neer dat ghi die onderste
figuere v der op verste nieten
moecht trecken
/ so ne
der op verste nieten
moecht trecken
/ so ne t een vander [fo.3. verso]
naerster figuer
t een vander [fo.3. verso]
naerster figuer ter slincker dat
waert /
e
ter slincker dat
waert /
e sal zijn 10 e
sal zijn 10 e addeerter de figuere toe die te cleene
was om de onderste
daeraf te trecken / ghelijc ic wil treck
addeerter de figuere toe die te cleene
was om de onderste
daeraf te trecken / ghelijc ic wil treck 6892 van 9721 stellet aldus
6892 van 9721 stellet aldus 1 dat is tghetal
v
1 dat is tghetal
v welck ghi 2 niet en const
ghetrecken / daeraf co
welck ghi 2 niet en const
ghetrecken / daeraf co t 9 die sedt
on
t 9 die sedt
on 2 voort
addeert 1 tot 9 co
2 voort
addeert 1 tot 9 co t 10 /e
t 10 /e 10 van 10 blijft 0 / daer toe addeert 2
die set
on
10 van 10 blijft 0 / daer toe addeert 2
die set
on de linie / e
de linie / e tot dat naeste getal als 8 tot 1
word
tot dat naeste getal als 8 tot 1
word 9. Segt 9 van 7 dat
en c
9. Segt 9 van 7 dat
en c niet ghesijn / maer van 10
blijft 1 e
niet ghesijn / maer van 10
blijft 1 e 7 word
7 word 8 die scrijft onder 8
ten lesten gheeft 1 tot 6 maect 7 e
8 die scrijft onder 8
ten lesten gheeft 1 tot 6 maect 7 e 7 ghetrock
7 ghetrock van 9 Reste 2 e
van 9 Reste 2 e staet
aldus
staet
aldus Die maniere van spreken.
Die maniere van spreken.
 Een ander maniere van substractie
de vierde regel.
Een ander maniere van substractie
de vierde regel.
 wildi treck
wildi treck 3008906 van 5006004
stelt deen bou
3008906 van 5006004
stelt deen bou dander als voren e
dander als voren e beghint van
beghint van slincker
hant. Segt 3 v
slincker
hant. Segt 3 v 5
blijft 2 die sou di on
5
blijft 2 die sou di on stellen waert
dat dye on
stellen waert
dat dye on ste somme niet
meer
ste somme niet
meer en bleue d
en bleue d de opperste / mer om datse meer
de opperste / mer om datse meer blijftso laet bou
blijftso laet bou de 5 een eenk
de 5 een eenk staen e
staen e doet de 5 wt met e
doet de 5 wt met e streepk
streepk / e
/ e stelt 1 on
stelt 1 on 3 e
3 e gaet een figure voort
e
gaet een figure voort
e segt 0 v
segt 0 v 10 blijft altijts 10
daer
10 blijft altijts 10
daer een figure voort
e
een figure voort
e sedt 9 on
sedt 9 on neffens 1 dan trect die
9 v
neffens 1 dan trect die
9 v die opperste
10. Rest 1 dit stelt bouen 0 om de cause voorseyt dan gaet een figuere voort /
e
die opperste
10. Rest 1 dit stelt bouen 0 om de cause voorseyt dan gaet een figuere voort /
e trect 0 van 10
sedt 9 onder laet 1 bou
trect 0 van 10
sedt 9 onder laet 1 bou als voren
/ gaet noch voort / e
als voren
/ gaet noch voort / e trect 8 v
trect 8 v 16 blijft 8 stelt 7
on
16 blijft 8 stelt 7
on e
e laet 1 bouen die 6 e
laet 1 bouen die 6 e doerstreept de 6 /daer
na trect 9 v
doerstreept de 6 /daer
na trect 9 v 10
Rest 1 stelt dat 1 bou
10
Rest 1 stelt dat 1 bou om de
cause [fo.4. recto] als voren e
om de
cause [fo.4. recto] als voren e stelt 0 onder e
stelt 0 onder e dan gaet voort e
dan gaet voort e trect 0 van 10 blijft 10
/ stelt we
trect 0 van 10 blijft 10
/ stelt we 9 onder
e
9 onder
e bou
bou daer nae ten lest
daer nae ten lest trect 6 v
trect 6 v 14 Rest 8 die sedt
on
14 Rest 8 die sedt
on e
e also rest v als ghi
trect 3008006 v
also rest v als ghi
trect 3008006 v 5006004 reste 1997998 also ghi hier siet int exempl
5006004 reste 1997998 also ghi hier siet int exempl .
. oft ghi
wel ghesubstraheert hebt. So addeert beyde de laetste somm
oft ghi
wel ghesubstraheert hebt. So addeert beyde de laetste somm te sam
te sam als betalinge e
als betalinge e reste e
reste e commet ghelijc die opperste somme te
wet
commet ghelijc die opperste somme te
wet de schult so yst
welgheda
de schult so yst
welgheda als dat blijct hier
onder.
als dat blijct hier
onder. Multiplicatie is hier ghedeylt inses
reghelen.
Multiplicatie is hier ghedeylt inses
reghelen.
 menighen met een ander ghetal / dat is
also veel
als den multiplicateur / of multipliceer
menighen met een ander ghetal / dat is
also veel
als den multiplicateur / of multipliceer in h
in h selven beuangt. So menich
werf te augmenteren oft menichfuldigen d
selven beuangt. So menich
werf te augmenteren oft menichfuldigen d nommer d
nommer d welcken ghemultipliceert
moet werd
welcken ghemultipliceert
moet werd . Exemplum. Ic wil
multiplicer
. Exemplum. Ic wil
multiplicer 3 met 2 e
3 met 2 e ic segge 3 werf 2 is 6
de 3 is d
ic segge 3 werf 2 is 6
de 3 is d multiplicator e
multiplicator e de 2 d
de 2 d nommer d
nommer d welck
welck ghemultipliceert moet
werd
ghemultipliceert moet
werd . E
. E om alle multiplicatie te do
om alle multiplicatie te do die on
die on tiene sijn / so heb ic
ghestelt een tafelk
tiene sijn / so heb ic
ghestelt een tafelk daer bi
datm
daer bi
datm terstont vind
terstont vind sal de multiplicacie v
sal de multiplicacie v 1
tot alle die figuer
1
tot alle die figuer totter
neghenster toe. Exempel. Ic wil multiplier
totter
neghenster toe. Exempel. Ic wil multiplier 7
werf 9 so neme ic 9 aen de slincke hant e
7
werf 9 so neme ic 9 aen de slincke hant e gae voort tot on
gae voort tot on 7 die bou
7 die bou int
opperste staet so vind ic 63 so veel maect 7 werf 9 e
int
opperste staet so vind ic 63 so veel maect 7 werf 9 e doet also van alle an
doet also van alle an ghelijck
ghelijck e
e dit is goet
dit is goet  iongers die eerst leeren [fo.4.
verso]
iongers die eerst leeren [fo.4.
verso] Die eerste reghele.
Die eerste reghele.
 2
figuer
2
figuer met eender figuere / als 24
met 4 so stelt 24 bouen e
met eender figuere / als 24
met 4 so stelt 24 bouen e 4
onder / e
4
onder / e segt 4 werf 4 is 16 /
stelt 6 on
segt 4 werf 4 is 16 /
stelt 6 on e
e hout 1 ind
hout 1 ind sin / daer na segt 4 werf 2 is 8 / hier
toe addeert 1 ind
sin / daer na segt 4 werf 2 is 8 / hier
toe addeert 1 ind sin co
sin co t 9 die 9 set achter 6 co
t 9 die 9 set achter 6 co t 96 so veel maect 4 werf 24 waer af de
si figuere hier na volghet.
t 96 so veel maect 4 werf 24 waer af de
si figuere hier na volghet.
 Die tweede reghel.
Die tweede reghel.
 2 figuer
2 figuer oft meer / met 2 figuren oft meer / als
ick wil multiplieren 25 met 36 stelt de
oft meer / met 2 figuren oft meer / als
ick wil multiplieren 25 met 36 stelt de bou
bou dan
dan als vor
als vor e
e segt 6 werf 5 is 30 stelt 0 on
segt 6 werf 5 is 30 stelt 0 on 6 e
6 e hout 3 ind
hout 3 ind sin / daer na segt 6 werf 2 is 12
e
sin / daer na segt 6 werf 2 is 12
e 3 ind
3 ind sin is 15 / die stelt al achter 0 / daer na
multipliceert metter 3 dat is met 30 e
sin is 15 / die stelt al achter 0 / daer na
multipliceert metter 3 dat is met 30 e segt 3 werf 5 is 15. Stelt de 5
een
segt 3 werf 5 is 15. Stelt de 5
een graet voor
graet voor achterwaert te wet
achterwaert te wet onder 5 / e
onder 5 / e hout 1 ind
hout 1 ind sin / dan segt 3 werf 2 is 6 / daer toe
addeert u 1 ind
sin / dan segt 3 werf 2 is 6 / daer toe
addeert u 1 ind sin co
sin co t 7 die stelt on
t 7 die stelt on 1 achter 5 daer na adderet de 2
somm
1 achter 5 daer na adderet de 2
somm te sam
te sam coemt 900 waer af die figuere
[fo. 5 recto]
hier na volgt.
coemt 900 waer af die figuere
[fo. 5 recto]
hier na volgt.
 Die derde reghele.
Die derde reghele.
 veel
figuer
veel
figuer met malcander
met malcander als ic wil multiplicer
als ic wil multiplicer 5378 met 6795. So stelt beyde
ghetal
5378 met 6795. So stelt beyde
ghetal deen bou
deen bou dander / so hier on
dander / so hier on volget / e
volget / e segt 5 werf 8 is 40 / stelt 0 onder 5
e
segt 5 werf 8 is 40 / stelt 0 onder 5
e hout 4 inden sin / daer na segt
we
hout 4 inden sin / daer na segt
we 5 werf 7 is 35 e
5 werf 7 is 35 e 4 ind
4 ind sin maect 39 / stelt 9 on
sin maect 39 / stelt 9 on 9 e
9 e hout 3 ind
hout 3 ind sin / daer na segt 5 werf 3 is 15
e
sin / daer na segt 5 werf 3 is 15
e 3 ind
3 ind sin is 18 / stelt 8 on
sin is 18 / stelt 8 on 7 e
7 e hout 1 ind
hout 1 ind sin ten laetsten segt 5 werf 5 es 25
e
sin ten laetsten segt 5 werf 5 es 25
e 1 ind
1 ind sin is 26 / stelt gheheel achter de 8
e
sin is 26 / stelt gheheel achter de 8
e coemt dan aldus.
coemt dan aldus.
 graet achterwaert sta
graet achterwaert sta / om dieswille datse staet inde plaetse
v
/ om dieswille datse staet inde plaetse
v 10. Nu segt 9 werf 8 is 72 /
sedt 2 on
10. Nu segt 9 werf 8 is 72 /
sedt 2 on 9 e
9 e hout 7 ind
hout 7 ind sin / d
sin / d multipliceert voort totter lester figuere
soot hier voorseyt is co
multipliceert voort totter lester figuere
soot hier voorseyt is co t voer de
multiplicacie van 9 coemt 48402 / e
t voer de
multiplicacie van 9 coemt 48402 / e staet dan aldus.
staet dan aldus.
 segt 7 werf 8 is 56 / stelt on
segt 7 werf 8 is 56 / stelt on 0
e
0
e hout 5 ind
hout 5 ind sin e
sin e werct also achteruolghende als
vor
werct also achteruolghende als
vor coemt voor dye multiplicacie
van
[fo. 5 verso]
7 . 37646 / daer na werct metter laetster figuere met 6 in al
coemt voor dye multiplicacie
van
[fo. 5 verso]
7 . 37646 / daer na werct metter laetster figuere met 6 in al manieren als voren e
manieren als voren e 6 werf 8 is 48 / stelt 8 onder 4 e
6 werf 8 is 48 / stelt 8 onder 4 e voort alsoot voorseyt is / co
voort alsoot voorseyt is / co t 32268 e
t 32268 e staet als hier na volght / dan addeert de
4 on
staet als hier na volght / dan addeert de
4 on ste somm
ste somm te samen co
te samen co t 36543510 alsoot blijct hier on
t 36543510 alsoot blijct hier on int exempl
int exempl .
.
 Die vierde reghel v
Die vierde reghel v multiplicatie een an
multiplicatie een an maniere
maniere 3576 met 6358.
So multipliceert 3576 met 6 dwelc is die leste figuere vander ander somme
co
3576 met 6358.
So multipliceert 3576 met 6 dwelc is die leste figuere vander ander somme
co t 21456 hier voren set 000
figueren om dieswille dat 6 / 3 figuer
t 21456 hier voren set 000
figueren om dieswille dat 6 / 3 figuer voer haer heeft coemt 21456000 / daer
nae multipliceert 3576 met 3 coemt 10728 / hier voren stelt 00 figuer
voer haer heeft coemt 21456000 / daer
nae multipliceert 3576 met 3 coemt 10728 / hier voren stelt 00 figuer 00 / om dat voor 3 maer 2 figuer
00 / om dat voor 3 maer 2 figuer en staen co
en staen co t 1072800 / daer na multipliceert 3576
met 5 co
t 1072800 / daer na multipliceert 3576
met 5 co t 17880 / stelt hier een
figure voor 0 co
t 17880 / stelt hier een
figure voor 0 co t 178800 / daer
na multipliceert metter lester figuere dat is 8 co
t 178800 / daer
na multipliceert metter lester figuere dat is 8 co t 28608 / nv addeert dese vier
somm
t 28608 / nv addeert dese vier
somm te sam
te sam / als 21456000 e
/ als 21456000 e 21456000 e
21456000 e 1072800 e
1072800 e 178800 e
178800 e 28608 coemt te samen 22736208.
28608 coemt te samen 22736208.
 Die vijfste reghel noch een ander
maniere van multiplicatie.
Die vijfste reghel noch een ander
maniere van multiplicatie.
 25 met 34 so
stelt deen bou
25 met 34 so
stelt deen bou dan
dan als voren e
als voren e segt 4 werf 5 is 20 / stelt 0 e
segt 4 werf 5 is 20 / stelt 0 e hout 2 ind
hout 2 ind sin / daer na segt 4 werf 2 is 8 e
sin / daer na segt 4 werf 2 is 8 e 2 ind
2 ind sin co
sin co t 10 die hout ooc ind
t 10 die hout ooc ind sin / daer na multipliceert 25 met 3
e
sin / daer na multipliceert 25 met 3
e segt 3 werf 5 is 15 e
segt 3 werf 5 is 15 e 10 ind
10 ind sin coemt 25 / set 5 achter 0 e
sin coemt 25 / set 5 achter 0 e hout 2 ind
hout 2 ind sin / daer na segt 3 werf 2 is 6 e
sin / daer na segt 3 werf 2 is 6 e 2 inden sin coemt 8 die stelt achter 5
e
2 inden sin coemt 8 die stelt achter 5
e coemt 850 / e
coemt 850 / e is ghemaect.
is ghemaect.
 Die seste reghele.
Die seste reghele.
 sommen daer
veel cyfers voor staen als wildi multiplicer
sommen daer
veel cyfers voor staen als wildi multiplicer 2100 met 34000 so multipliceert 21
met 34 co
2100 met 34000 so multipliceert 21
met 34 co t 714 daer toe stelt
also vele cyfers voor
t 714 daer toe stelt
also vele cyfers voor als aen
beyde de sommen staen dat syn 00000 co
als aen
beyde de sommen staen dat syn 00000 co t 71400000 / doet desghelijcx van
ander.
t 71400000 / doet desghelijcx van
ander.
 Die proeue van multiplicatie.
Die proeue van multiplicatie.
 oft ghi wel
ghemultipliceert hebt / so deylt beyde dopperste somm
oft ghi wel
ghemultipliceert hebt / so deylt beyde dopperste somm de simpel n
de simpel n mers bi 9 elcke somme bison
mers bi 9 elcke somme bison e
e werpt de 9 altijts wech e
werpt de 9 altijts wech e de reste v
de reste v elcke somme multipliceert te sam
elcke somme multipliceert te sam / e
/ e vand
vand producte werpt ooc de 9 wech e
producte werpt ooc de 9 wech e de reste stelt opt cruce / exempel. Ic wil
proeu
de reste stelt opt cruce / exempel. Ic wil
proeu oft de leste multiplicacie op
2 na goet is so neme ick beyde dye opperste sommen als 3576 e
oft de leste multiplicacie op
2 na goet is so neme ick beyde dye opperste sommen als 3576 e 6358 e
6358 e segghe 3 e
segghe 3 e 5 is 8 e
5 is 8 e 7
[fol. 6 verso]
coemt 15 e
7
[fol. 6 verso]
coemt 15 e 9 vvt / rest 6 e
9 vvt / rest 6 e 6 coemt 12 de 9 vvt blijft 3 die stelt
opt cruyce / daer na deylt oft telt de 9 vvt 6358 e
6 coemt 12 de 9 vvt blijft 3 die stelt
opt cruyce / daer na deylt oft telt de 9 vvt 6358 e segt 6 e
segt 6 e 3 is 9 blijft niet / daer na 5 e
3 is 9 blijft niet / daer na 5 e 8 is 13 e
8 is 13 e 9 vvt blijft 4 die stelt on
9 vvt blijft 4 die stelt on cruyce e
cruyce e multipliceert 3 met 4 co
multipliceert 3 met 4 co t 12 daer 9 vvt blijft 3 stelt 3 ter
sid
t 12 daer 9 vvt blijft 3 stelt 3 ter
sid aen tcruyce / d
aen tcruyce / d ouertelt die figuer
ouertelt die figuer van der lester somme die ghesuecedeert
is vvter multiplicatie / als 22736208 / e
van der lester somme die ghesuecedeert
is vvter multiplicatie / als 22736208 / e segt 2 e
segt 2 e 2 is 4 e
2 is 4 e 7 is 11 de 9 wech blijft 2 e
7 is 11 de 9 wech blijft 2 e 3 is 5 e
3 is 5 e 6 is 11 de 9 vvt blijft ooc 2 e
6 is 11 de 9 vvt blijft ooc 2 e 2 is 4 e
2 is 4 e 8 is 12 dye 9 wech blijft 3 die stelt op
dan
8 is 12 dye 9 wech blijft 3 die stelt op
dan side vand
side vand cruyce co
cruyce co t ghelijck op deen side vand
t ghelijck op deen side vand cruyce staet e
cruyce staet e is wel gheda
is wel gheda . Mer alst onghelijc co
. Mer alst onghelijc co t so bethoget dat qualijck ghewrocht is /
doet aldus van alle ander multiplicatien.
t so bethoget dat qualijck ghewrocht is /
doet aldus van alle ander multiplicatien.