door
Dr. P.J.H. Baudet


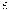
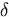 -definitie
zou willen noemen, van de behandelingswijze van
WALLIS verschillend, er is een nog veel dieper gaand verschil,
dat reeds daaruit blijkt, dat het onmogelijk zou zijn op grond
van de behandelingswijze van WALLIS eenige eigenschap der
limieten te bewijzen8).
-definitie
zou willen noemen, van de behandelingswijze van
WALLIS verschillend, er is een nog veel dieper gaand verschil,
dat reeds daaruit blijkt, dat het onmogelijk zou zijn op grond
van de behandelingswijze van WALLIS eenige eigenschap der
limieten te bewijzen8).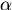 , waarin
, waarin
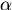 een willekeurig positief getal
beduidt. Eene verbinding van
zijne werkwijze met die van ARCHIMEDES zou hebben kunnen
voeren tot het tegenwoordige limietbegrip.
[pag. 12]
een willekeurig positief getal
beduidt. Eene verbinding van
zijne werkwijze met die van ARCHIMEDES zou hebben kunnen
voeren tot het tegenwoordige limietbegrip.
[pag. 12]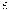
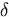 definitie nog niet formeel opstelt, hetgeen dan ook de oorzaak is van het
uitspreken van een onjuiste stelling, welke hij in 1853 verbeterd heeft en
waarop wij nog terugkomen.
definitie nog niet formeel opstelt, hetgeen dan ook de oorzaak is van het
uitspreken van een onjuiste stelling, welke hij in 1853 verbeterd heeft en
waarop wij nog terugkomen.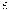
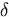 definitie uitgaat. Immers, men bewijst, dat er voor elke positieve
definitie uitgaat. Immers, men bewijst, dat er voor elke positieve
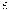 een
een
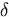 van de gevraagde hoedanigheid bestaat,
zoodat men een oneindig aantal oordeelen uitspreekt. In verband met het feit,
dat het onmogelijk is, dit te reduceeren tot een eindig aantal oordeelen,
schijnt het mij toe, dat juist hieraan het limiet-oordeel zijn buitengewone
beteekenis ontleent.
van de gevraagde hoedanigheid bestaat,
zoodat men een oneindig aantal oordeelen uitspreekt. In verband met het feit,
dat het onmogelijk is, dit te reduceeren tot een eindig aantal oordeelen,
schijnt het mij toe, dat juist hieraan het limiet-oordeel zijn buitengewone
beteekenis ontleent.
 definitie nog niet bezat, anderdeels daaraan, dat de theorie van het
irrationale getal, welke toen nog niet ontwikkeld was, aan eene bewijsvoering
moet voorafgaan. Haar beteekenis heeft hij daarentegen volkomen doorgrond. Dit
blijkt ten duidelijksten uit de wijze, waarop hij haar herhaaldelijk toepast
9).
definitie nog niet bezat, anderdeels daaraan, dat de theorie van het
irrationale getal, welke toen nog niet ontwikkeld was, aan eene bewijsvoering
moet voorafgaan. Haar beteekenis heeft hij daarentegen volkomen doorgrond. Dit
blijkt ten duidelijksten uit de wijze, waarop hij haar herhaaldelijk toepast
9).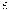
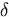 definitie van het limietbegrip.
definitie van het limietbegrip.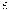
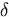 terminologie uit en het is niet wel te zien hoe men een bruikbare definitie van
uniforme limietovergang in het algemeen zou kunnen geven, zonder de
terminologie uit en het is niet wel te zien hoe men een bruikbare definitie van
uniforme limietovergang in het algemeen zou kunnen geven, zonder de
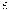
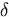 formulering.
formulering.Edelgrootachtbare Heeren Curatoren dezer Hoogeschool,
Hooggeleerde Heeren Profesoren der Technische Hoogeschool,
Hooggeachte Ambtgenooten van de Afdeeling der Algemeene Wetenschappen,
Hooggeleerde Schuh, Hoogvereerde Mentor,
Dames en Heeren Studenten aan de Technische Hoogeschool,
Ik heb gezegd.