

 bezeichne, mögen
die folgenden Blätter als ein Versuchm die Wissenschaft der Zahlen auf
einheitlicher Grundlage zu errichten, wohlwollende Aufnahme finden, und
mögen sie andere Mathematiker dazu anregen, die langen Reihen von
Schlüssen auf ein bescheideneres, angenehmeres Maß
zurückzuführen.
bezeichne, mögen
die folgenden Blätter als ein Versuchm die Wissenschaft der Zahlen auf
einheitlicher Grundlage zu errichten, wohlwollende Aufnahme finden, und
mögen sie andere Mathematiker dazu anregen, die langen Reihen von
Schlüssen auf ein bescheideneres, angenehmeres Maß
zurückzuführen.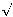 2 .
2 .
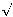 3 =
3 =
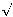 6 sei noch nirgends streng
bewiesen, auch in Hinsicht auf dieses, in mancher anderen Beziehung treffliche
Werk, welches ich damals noch nicht kannte, für gerechtfertigt
halte.
6 sei noch nirgends streng
bewiesen, auch in Hinsicht auf dieses, in mancher anderen Beziehung treffliche
Werk, welches ich damals noch nicht kannte, für gerechtfertigt
halte.R. Dedekind.
R. Dedekind.
R. Dedekind.
| Seite | ||
| Vorwort | III-XIII | |
| §. 1. | Systeme von Elementen | 1 |
| §. 2. | Abbildung eines Systems | 6 |
| §. 3. | Aehnlichkeit einer Abbildung. Aehnliche Systeme | 8 |
| §. 4. | Abbildung eines Systems in sich selbst | 11 |
| §. 5. | Das Endliche und Unendliche | 17 |
| §. 6. | Einfach unendliche Systeme. Reihe der natürlichen Zahlen | 20 |
| §. 7. | Größere und kleinere Zahlen | 22 |
| §. 8. | Endliche und unendliche Theile der Zahlenreihe | 31 |
| §. 9. | Definition einer Abbildung de Zahlenreihe durch Induction | 33 |
| §. 10. | Die Classe der einfach undendlichen Systeme | 40 |
| §. 11. | Addition der Zahlen | 43 |
| §. 12. | Multiplication der Zahlen | 47 |
| §. 13. | Potenzirung der Zahlen | 49 |
| §. 14. | Anzahl der Elemente eines endlichen Systems | 51 |
 eines Systems
S wird ein Geseß verstanden, nach welchem zu jedem
bestimmten Element s von S ein bestimmtes Ding
gehört, welches das Bild von s heißt und mit
eines Systems
S wird ein Geseß verstanden, nach welchem zu jedem
bestimmten Element s von S ein bestimmtes Ding
gehört, welches das Bild von s heißt und mit
 (s) bezeichnet wird; wir
sagen auch, daß
(s) bezeichnet wird; wir
sagen auch, daß  (s)
dem Element s entspricht, daß
(s)
dem Element s entspricht, daß
 (s) durch die Abbildung
(s) durch die Abbildung
 aus s entsteht
oder erzeugt wird, daß s durch die Abbildung
aus s entsteht
oder erzeugt wird, daß s durch die Abbildung
 in
in
 (s)
übergeht. Ist nun T irgend ein Theil von
S, so ist in der Abbildung
(s)
übergeht. Ist nun T irgend ein Theil von
S, so ist in der Abbildung
 von S zugleich eine
bestimmte Abbildung von T enthalten, welche der einfachheit wegen
wohl mit demselben Zeichen
von S zugleich eine
bestimmte Abbildung von T enthalten, welche der einfachheit wegen
wohl mit demselben Zeichen  bezeichnet werden darf und darin besteht, daß jedem Elemente
t des Systems T dasselbe Bild
bezeichnet werden darf und darin besteht, daß jedem Elemente
t des Systems T dasselbe Bild
 (t) entspricht, welches
t als Element von S besißt; zugleich soll das System,
welches aus allen Bildern
(t) entspricht, welches
t als Element von S besißt; zugleich soll das System,
welches aus allen Bildern  (t)
besteht, das Bild von T heißen und mit
(t)
besteht, das Bild von T heißen und mit
 (T) bezeichnet werden,
wodurch auch die Bedeutung von
(T) bezeichnet werden,
wodurch auch die Bedeutung von
 (S) erklärt ist. Als ein
Beispiel einer Abbildung eines Systems ist schon die Belegung seiner Elemente
mit bestimmten Zeichen oder Namen anzusehen. Die einfachste Abbildung eines
Systems ist diejenige, durch welche jedes Element in sich selbst übergeht;
sie soll die identische Abbildung des Systems heißen. Der
Bequemlichkeit halber wollen wir in den folgenden Säßen 22, 23,
24, die sich auf eine beliebige Abbildung
(S) erklärt ist. Als ein
Beispiel einer Abbildung eines Systems ist schon die Belegung seiner Elemente
mit bestimmten Zeichen oder Namen anzusehen. Die einfachste Abbildung eines
Systems ist diejenige, durch welche jedes Element in sich selbst übergeht;
sie soll die identische Abbildung des Systems heißen. Der
Bequemlichkeit halber wollen wir in den folgenden Säßen 22, 23,
24, die sich auf eine beliebige Abbildung
 eines beliebigen Systems S
beziehen, die Bilder von Elementen s und Theilen T
entsprechend durch s' und T' bezeichnen; außerdem
seßen wir fest, daß kleine und große lateinische Buchstaben
ohne Accent immer Elemente und Theile dieses Systems S bedeuten
sollen. [pag. 7]
eines beliebigen Systems S
beziehen, die Bilder von Elementen s und Theilen T
entsprechend durch s' und T' bezeichnen; außerdem
seßen wir fest, daß kleine und große lateinische Buchstaben
ohne Accent immer Elemente und Theile dieses Systems S bedeuten
sollen. [pag. 7] eine Abbildung eines Systems
S, und
eine Abbildung eines Systems
S, und  eine Abbildung des
Bildes S' =
eine Abbildung des
Bildes S' =  (S),
so entspringt hieraus immer eine aus
(S),
so entspringt hieraus immer eine aus
 und
und
 zusammengeseßte
9) Abbildung
zusammengeseßte
9) Abbildung
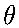 von S, welche darin
besteht, daß jedem Elemente s von S das Bild
von S, welche darin
besteht, daß jedem Elemente s von S das Bild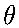 (s) =
(s) =
 (s') =
(s') =
 (
( (s))
(s))
 (s) = s'
geseßt ist. Diese Abbildung
(s) = s'
geseßt ist. Diese Abbildung
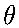 kann kurz durch das Symbol
kann kurz durch das Symbol
 .
. oder
oder

 , das Bild
, das Bild
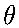 (s) durch
(s) durch

 (s) bezeichnet werden, wobei auf
die Stellung der Zeichen
(s) bezeichnet werden, wobei auf
die Stellung der Zeichen
 ,
,
 wohl zu achten ist, weil das Zeichen
wohl zu achten ist, weil das Zeichen

 im Allgemeinen bedeutungslos ist und nur
dann einen Sinn hat, wenn
im Allgemeinen bedeutungslos ist und nur
dann einen Sinn hat, wenn
 (S')
(S')
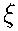 eine Abbildung des Systems
eine Abbildung des Systems
 (S') =
(S') =

 (S), und
(S), und
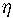 die aus
die aus
 und
und
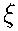 zusammengeseßte Abbildung
zusammengeseßte Abbildung
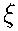
 des Systems S', so ist
des Systems S', so ist
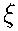
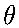 (s) =
(s) =
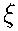
 (s') =
(s') =
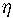 (s') =
(s') =
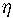
 (s), also stimmen die
zusammengeseßten Abbildungen
(s), also stimmen die
zusammengeseßten Abbildungen
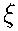
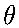 und
und
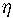
 für jedes Element s von
S mit einander überein, d.h. es ist
für jedes Element s von
S mit einander überein, d.h. es ist
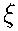
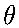 =
=
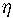
 . Dieser Saß kann nach der Bedeutung
von
. Dieser Saß kann nach der Bedeutung
von 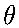 und
und
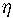 füglich durch
füglich durch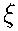 .
.
 =
=
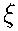
 .
.
 ,
,
 ,
, 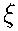 zusammengeseßte Abbildung kann kurz
durch
zusammengeseßte Abbildung kann kurz
durch 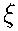

 bezeichnet werden.
bezeichnet werden. eines Systems S
heißt ähnlich (oder deutlich), wenn
verschiedene Elementen a, b des Systems S
stets verschiedene Bilder a' =
eines Systems S
heißt ähnlich (oder deutlich), wenn
verschiedene Elementen a, b des Systems S
stets verschiedene Bilder a' =
 (a), b' =
(a), b' =
 (b) entsprechen. Da in
diesem Falle umgekehrt aus s' = t' stets s =
t folgt, so ist jedes Element des Systems S' =
(b) entsprechen. Da in
diesem Falle umgekehrt aus s' = t' stets s =
t folgt, so ist jedes Element des Systems S' =
 (S) das Bild s'
von einem einzigen, vollständig bestimmten Elemente s des
Systems S, und man kann daher der Abbildung
(S) das Bild s'
von einem einzigen, vollständig bestimmten Elemente s des
Systems S, und man kann daher der Abbildung
 von S eine
umgekehrte, etwa mit
von S eine
umgekehrte, etwa mit
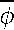 zu bezeichnende Abbildung des
Systems S' gegenüberstellen, welche darin besteht, daß
jedem Elemente s' von S' das Bild
zu bezeichnende Abbildung des
Systems S' gegenüberstellen, welche darin besteht, daß
jedem Elemente s' von S' das Bild
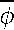 (s') = s
entspricht, und offenbar ebenfalls ähnlich ist. Es leuchtet ein, daß
(s') = s
entspricht, und offenbar ebenfalls ähnlich ist. Es leuchtet ein, daß
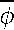 (S') = S,
daß ferner
(S') = S,
daß ferner  die zu
die zu
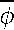 gehörige umgekehrte
Abbildung, und daß die nach 25 aus
gehörige umgekehrte
Abbildung, und daß die nach 25 aus
 und
und
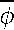 zusammengeseßte
[pag. 9] Abbildung
zusammengeseßte
[pag. 9] Abbildung
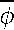
 die identische Abbildung von S ist
(21). Zugleich ergeben sich folgende Ergänzungen zu §. 2 unter
Beibehaltung der dortigen Bezeichnungen.
die identische Abbildung von S ist
(21). Zugleich ergeben sich folgende Ergänzungen zu §. 2 unter
Beibehaltung der dortigen Bezeichnungen. eine ähnliche Abbildung von
S, und
eine ähnliche Abbildung von
S, und  eine ähnliche
Abbildung von
eine ähnliche
Abbildung von  (S), so ist
die aus
(S), so ist
die aus  und
und
 zusammengeseßte Abbildung
zusammengeseßte Abbildung

 von S ebenfalls eine
ähnliche, und die zugehörige umgekehrte Abbildung
von S ebenfalls eine
ähnliche, und die zugehörige umgekehrte Abbildung
 (a), b' =
(a), b' =
 (b), und diesen wieder
verschiedene Bilder
(b), und diesen wieder
verschiedene Bilder  (a') =
(a') =

 (a),
(a),
 (b') =
(b') =

 (b), also ist [pag. 10]
(b), also ist [pag. 10]

 eine ähnliche Abbildung.
Außerdem geht jedes Element
eine ähnliche Abbildung.
Außerdem geht jedes Element

 (s) =
(s) =
 (s') des Systems
(s') des Systems

 (S) durch
(S) durch
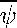 in s' =
in s' =
 (s) und dieses durch
(s) und dieses durch
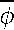 in s über, also
geht
in s über, also
geht 
 (s) durch
(s) durch
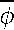
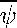 in s über,
w.z.b.w.
in s über,
w.z.b.w. von
S giebt, daß
von
S giebt, daß
 (S) = R, also
auch
(S) = R, also
auch 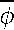 (R) =
S wird. Offenbar ist nach 30 jedes System sich selbst
ähnlich.
(R) =
S wird. Offenbar ist nach 30 jedes System sich selbst
ähnlich. ,
,
 solche ähnliche Abbildungen
von S, R, daß
solche ähnliche Abbildungen
von S, R, daß
 (S) = R,
(S) = R,
 (R) = Q wird, so
ist (nach 31)
(R) = Q wird, so
ist (nach 31) 
 eine solche ähnliche Abbildung von
S, daß
eine solche ähnliche Abbildung von
S, daß 
 (S) = Q wird,
w.z.b.w.
(S) = Q wird,
w.z.b.w. eine ähnliche Abbildung von
S,
eine ähnliche Abbildung von
S,  (S) =
R, und T
(S) =
R, und T  (T)
(T)
 (s) nach 27 nicht in
(s) nach 27 nicht in
 (T) enthalten sein; mithin
ist
(T) enthalten sein; mithin
ist  (T) echter Theil von
R, w.z.b.w. [pag. 11]
(T) echter Theil von
R, w.z.b.w. [pag. 11]